变量可以是矩阵吗_工具变量法

人大计量老师的专题干货！！！

--- ---- --- --- ----

工具变量法主要是针对性解决，违背经典线性回归假定情况之一—内生性—问题的。

什么是内生性？

• 内生性是指解释变量和误差项ε存在相关性，导致最小二乘估计的参数β有偏非一致。统计学上不太喜欢不一致的东西，因为大数定律和中心极限定理都是假定样本在样本量无穷大的情况下，无限接近于真实总体；样本统计量（估计量）无限接近总体参数（待估参数）。

什么情况下会产生内生性？

• 遗漏重要解释变量
• 联立方程问题，y可以解释x，x也可以解释y
• 测量误差，观测到的X,y与真实的X和y存在一定的差距

，X为n×p的矩阵，β为p维系数向量.

工具变量的要求

工具变量法的性质

• 大样本条件下，是一致估计。
• 小样本下，不是无偏估计。

普通最小二乘VS工具变量估计

工具变量法的一般形式

其中，W为工具变量矩阵、R为权矩阵。

①广义最小二乘估计

不满足误差同方差的假定时

，当

，则工具变量估计为GLSIV估计：

注：广义最小二乘估计获得的同时是最优估计，β参数的方差最小。

②两阶段最小二乘估计

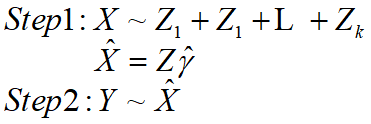
当

时，则工具变量估计是2SLS估计：

我们可以发现当Ω=I（单位阵），利用两阶段最小二乘估计获得的是最优估计。

Wu_Hausman检验的原理

原假设：无内生性

IV估计

在有无内生性的条件下，都是无偏的。

OLS估计

在有内生性的条件下，是有偏的，而在无内生性的条件下，是无偏的。

由这个式子可知，工具变量虽然克服了非一致的问题，但是牺牲了估计量的精度。

因为X和Z的相关性不可能达到1，因此IV估计的方差必然大于OLS估计的方差。

检验统计量的构造思想，β1和β2没有差别的话就没有内生性，差别过大就说明存在内生性：

实证过程中的内生性检验的具体步骤：

（1）将初步认为是内生的主解释变量作为被解释变量，将拟选的工具变量和其它外生解释变量作为解释变量进行回归，得到回归残差Resid；

（2）将残差Resid和所有的解释变量放入主回归方程进行回归（包括内生的主解释变量和其他外生解释变量，但不包含拟选的工具变量），如果残差项Resid的回归系数显著，则说明主解释变量确实是具有内生性。

HansenJ检验的原理（过度识别检验）

正规方程组

待估参数p+1，方程个数p+1，存在唯一解。

什么是过度识别？

1. 恰好识别：方程个数n=待估参数个数p，正规方程组存在唯一解；
2. 不可识别：方程个数n<待估参数个数p，正规方程组存在无穷多组解；（计量里一般不研究这种情况，假如你的模型存在多组参数，岂不是很奇怪？到底用哪一组呢？）
3. 过度识别：方程个数n>待估参数个数p，正规方程组不存在同时满足所有方程的解，在线代里就是无解的情况。（计量里，觉得这种情况可以容忍的，尽量找到一组参数尽可能近似满足所有的方程。）

过度识别检验统计量的构造思想是：(上述方程组的=都变成≈，平方和尽可能接近0）

原假设：工具变量的选取是合适的。

不拒绝原假设的表现，检验统计量不是显著异于0

注：恰好识别，检验统计量恒为0，该检验是在过度识别的前提下，检验工具变量的选取是否合适。

码字不易，点个赞再走o((>ω< ))o

欢迎评论讨论，指正错误。。。