（1小时数据结构）数据结构c++描述（二十五） --- 图（BFS遍历与 DFS遍历）

最新推荐文章于 2023-04-14 20:34:19 发布

比卡丘不皮

最新推荐文章于 2023-04-14 20:34:19 发布

阅读量491

点赞数 2

分类专栏：数据结构与算法文章标签：图数据结构 c++ DFS BFS

请转载请声明转载的地址

本文链接：https://blog.csdn.net/weixin_42126427/article/details/107860588

版权

数据结构与算法专栏收录该内容

42 篇文章 20 订阅

订阅专栏

图的基本概念：

简单地说，图（graph）是一个用线或边连接在一起的顶点或节点的集合。
如下图：

其中a 是无向图，c是有向图。

完全图:

权和网的含义

在某些实际场景中，图中的每条边（或弧）会赋予一个实数来表示一定的含义，这种与边（或弧）相匹配的实数被称为"权"，而带权的图通常称为网。如图 3 所示，就是一个网结构：

子图：指的是由图中一部分顶点和边构成的图，称为原图的子图。

图的常见存储结构：

无向图和有向图最常用的描述方法都是基于邻接的方式：邻接矩阵，邻接压缩表和邻接链表。
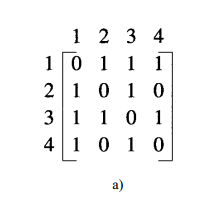
邻接矩阵：

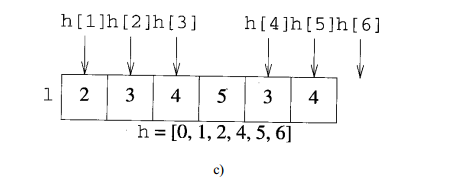
邻接压缩表：

邻接链表：

本篇文章使用的是邻接链表的方式来写的图

节点定义：

template<class T>
class ENode
{
public:
	int vertex; //边的一端顶点
	int adjVex; //边的另一端顶点
	T   weight; //边的权重
	ENode<T> *next; 

	ENode() { next = NULL; }
	ENode(int vertex, int adjvertex, T w, ENode<T> *nextArc)
	{
		this->vertex = vertex;
		adjVex = adjvertex;
		weight = w;
		next = nextArc;
	}
	operator T() const { return weight; }
	bool operator <(const ENode<T> &rhs) const 
	{
		return this->weight > rhs.weight;   //最小值优先
	}

};

连同图类定义：

目前学习BFS 与 DFS这部分可以先不看，这个是关于动态连通性后面的算法。

//自定义优先队列less的比较函数
template<class T>
class cmp
{
public:
	bool operator()(const ENode<T> &a, const ENode<T> &b) const 
	{
		return a.weight > b.weight;
	}
};

//对于输入的“点-点”数据,求出动态连通性
class UnionFind
{
private:
	int *id;    //父链接数组,由触点索引
	int *sz;    //由触点索引的各个根节点所对应的分量的大小
	int count;  //连通分量的数量
public:
	UnionFind(int N);
	~UnionFind();
	int Find(int p);                //找p所在连通分量的根
	bool Connected(int p, int q);   //p和q是否在同一个连通分量里
	int GetCount();                 //返回连通分量
	void Union(int p, int q);       //将p和q连接起来
};

UnionFind::UnionFind(int N) :count(N) 
{
	id = new int[N];
	sz = new int[N];
	for (int i = 0; i < N; ++i) {
		id[i] = i;
	}
	for (int j = 0; j < N; ++j) {
		sz[j] = 1;
	}
}

 UnionFind::~UnionFind()
{
	 delete[] id;
	 delete[] sz;
}
 //找p所在连通分量的根
 int UnionFind::Find(int p)
 {
	 while (p != id[p]) {
		 p = id[p];
	 }
	 return p;
 }
 //p和q是否在同一个连通分量里
bool UnionFind::Connected(int p, int q)
 {
	int pRoot = Find(p);
	int qRoot = Find(q);
	if (pRoot == qRoot) {
		return true;
	}
	else {
		return false;
	}
 }
//返回连通分量
int UnionFind::GetCount()
 {
	return count;

 }
//将p和q连接起来
void UnionFind::Union(int p, int q)
 {
	int pRoot = Find(p);
	int qRoot = Find(q);

	if (pRoot == qRoot) {   //已经在同个连通分量里,直接返回
		return;
	}
	else {                //将元素较少的连通分量连接到元素较多的连通分量上
		if (sz[pRoot] < sz[qRoot]) {
			id[pRoot] = qRoot;
			sz[qRoot] += sz[pRoot];
		}
		else {
			id[qRoot] = pRoot;
			sz[pRoot] += sz[qRoot];
		}
		count--;            //现有连通分量个数减1
	}
 }

图的类定义：

//图类
template <typename T>
class Graph
{
public:
	Graph(int mSize);
	~Graph();
	bool Exist(int u, int v) const;  //边u->v是否存在
	bool Insert(int u, int v, T w);   //插入边u->v
	bool Remove(int u, int v);       //删去边u->v
	void Reverse();             //得到反向图
	void DFS();                     //公有接口,深度优先搜索
	void BFS();                     //公有接口,宽度优先搜索

	bool HasCycle();                //判断是否有环
	stack<int> GetCycle();          //返回环
	void CalReversePost();          //通过递归调用DFSForReversePost来求得
	void TopoSort();                //拓扑排序
	void TopoSortByDFS();           //用DFS来求拓扑序列
	stack<int> GetReversePost();    //返回DFS中顶点的逆后序序列
	void CalculateConnection();     //求图的强连通分量
	int GetConnectedCount();        //得到强连通分量数
	int ConnectionID(int v);        //v所在的强连通分量的标识符(1~connectedCount)
	void ShowConnection();          //打印强连通分量
	void TarjanForConnection();     //用tarjan算法求强连通分量


	void Prim(int v0);              //普里姆算法求无向图最小代价生成树,外部接口
	void Kruskal();                 //克鲁斯卡尔算法求无向图最小代价生成树,外部接口
	void Dijkstra(int v0);          //迪杰斯特拉算法解决单源最短路径问题
	void Floyd();                   //弗洛伊德算法求所有顶点之间的最短路径
	T GetWeight(int u, int v);       //获得边u-v的权值

private:
	ENode<T> **enodes;
    Graph<T> *R;            //用于存放反向图
	int n;                  //顶点个数
	int edges;              //边的个数
	int connectedCount;     //强连通分量个数
	int *id;                //由顶点索引的数组,存放顶点所属的连通分量标识符
	vector<int> *tarjanConnection;    //通过tarjan算法得到的强连通分量
	int connectedCountForTarjan;      //在tarjan算法中使用的强连通分量个数
	bool hasCycle;          //是否有环
	stack<int> cycle;       //有向环中的所有顶点（如果存在）
	stack<int> reversePost; //通过DFS得到的所有顶点的逆后序排列
	UnionFind *uf;           //用于Kruskal算法,用来判断最小生成树森林中是否会构成回路
	void DFS(int v, bool *visited);              //私有DFS,供递归调用
	void BFS(int v, bool *visited);  //私有BFS

	void DFSForCycle(int v, bool *visited, bool *onStack, int *edgeTo);    //用DFS思想来判断环
	void DFSForReversePost(int v, bool *visited);   //用DFS思想来求逆后序序列,用于求拓扑序列或者强连通分量
	void DFSForConnection(int v, bool *visited); //用DFS思想来求强连通分量
	void TarjanForConnection(int u, bool *visited, int *DFN, int *low, stack<int> *tarjanStack, bool *inStack, int &index); //用tarjan算法求强连通分量,其实也是运用了DFS思想

	void ClearCycle();  //清空栈cycle中的记录
	void ClearReversePost();   //清空栈reversePost中的记录
	void CalInDegree(int *inDegree);    //计算所有顶点的入度

	void Prim(int v0, int *nearest, T *lowcost);  //普里姆算法求无向图最小代价生成树,私有,内部调用
	void Kruskal(priority_queue<ENode<T>> &pq); //克鲁斯卡尔算法求无向图最小代价生成树,私有,内部调用
	void Dijkstra(int v0, int  *path, T *curShortLen);    //迪杰斯特拉算法解决单源最短路径问题,私有,内部调用
	int FinMinLen(T *curShortLen, bool *mark);   //Dijkstra算法的辅助函数,用于找出下一条最短路径的终点

};

这里的图类包含了图的很多算法，本章先讲解最简单的部分，后期会慢慢更新。

图的构造（析构）函数：

template<typename T>
 Graph<T>::Graph(int mSize)
{
	 n = mSize;
	 edges = 0;
	 connectedCount = 0;
	 hasCycle = false;
	 enodes = new ENode<T> *[n];
	 id = new int[n];
	 for (int i = 0; i < n; ++i) {
		 enodes[i] = NULL;
		 id[i] = 0;
	 }
	 uf = new UnionFind(n);
     R = NULL;
	 tarjanConnection = new vector<int>[n]; //最多有n个
}

template<typename T>
 Graph<T>::~Graph()
{
	 ENode<T> *p, *q;
	 for (int i = 0; i < n; ++i) {
		 p = enodes[i];
		 while (p) {
			 q = p;
			 p = p->next;
			 delete (q);
		 }
	 }
	 delete[] enodes;
	 delete[] id;
	 delete uf;

}

Exist 函数：

 //边u->v是否存在
template<typename T>
bool Graph<T>::Exist(int u, int v) const
{
	if (u < 0 || v < 0 || u > n - 1 || v > n - 1 || u == v) {
		return false;   //输入参数无效
	}
	ENode<T> *p = enodes[u];
	while (p && p->adjVex != v) {
		p = p->next;
	}
	if (p) {
		return true;
	}
	else {
		return false;
	}
}

Insert函数：

//插入边u->v
template<typename T>
bool Graph<T>::Insert(int u, int v, T w)
{
	if (u < 0 || v < 0 || u > n - 1 || v > n - 1 || u == v) {
		return false;   //输入参数无效
	}
	if (Exist(u, v)) {
		cout << "Duplicate" << endl;
		return false;
	}
	else {
		//将新边结点插在由指针enodes[u]所指示的单链表最前面
		ENode<T> *p = new ENode<T>(u, v, w, enodes[u]); //第4个参数是next值，代码采用前插入
		enodes[u] = p;
		edges++;
		return true;
	}
}

删除函数：

//删去边u->v
template<typename T>
bool Graph<T>::Remove(int u, int v)
{
	if (u < 0 || v < 0 || u > n - 1 || v > n - 1 || u == v) {
		return false;   //输入参数无效
	}
	ENode<T> *p = enodes[u];
	ENode<T> *q = NULL;
	while (p && p->adjVex != v) {
		q = p;
		p = p->next;
	}
	if (!p) {
		cout << "Not exist." << endl;
		return false;
	}
	if (p == enodes[u]) {
		q = p;
		enodes[u] = p->next;
		delete (q);
		edges--;
	}
	else {
		q->next = p->next;
		delete (p);
		edges--;
	}
	return true;
}

Reverse反向图：

template<typename T>
void  Graph<T>::Reverse()
{
	for (int i = 0; i < n; ++i) {
		for (ENode<T> *w = enodes[i]; w; w = w->next) {
			R->Insert(w->adjVex, i, w->weight);
		}
	}

}

宽度优先搜索：

宽度优先搜索也叫广度优先搜索，考察图12-19a 中的有向图。判断从顶点 1出发可到达的所有顶点的一种方法是首先确定邻接于顶点1的顶点集合，这个集合是 { 2 , 3 , 4 }。然后确定邻接于 { 2 , 3 , 4 }的新的顶点集合，这个集合是{ 5 , 6 , 7 }。邻接于{ 5 , 6 , 7 }的顶点集合为{ 8 , 9 }，而不存在邻接于{ 8 , 9 }的顶点。因此，从顶点1出发可到达的顶点集合为{ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 }。

广度搜索 BFS：

//广度或教宽度
template<typename T>
void Graph<T>::BFS()
{
	bool * visited = new bool[n];
	for (int i = 0; i < n; ++i) {
		visited[i] = false;
	}

	for (int j = 0; j < n; ++j) {
		if (!visited[j]) {
			BFS(j, visited);
		}
	}
	delete[] visited;
}

template<typename T>
 void Graph<T>::BFS(int v, bool * visited)
{
	 visited[v] = true;
	 cout << v << " ";
	 queue<int> myqueue;
	 myqueue.push(v);  //进队列，

	 int s;
	 while (!myqueue.empty())
	 {
		 s = myqueue.front();
		 myqueue.pop();

		 for (ENode<T> * w = enodes[s]; w; w = w->next)
		 {
			 if (!visited[w->adjVex])
			 {
				 visited[w->adjVex] = true;
				 cout << w->adjVex << " ";
				 myqueue.push(w->adjVex);
			 }
		 }
	 }
}

简单的说明一下，首先visited 都是false，找到谁，就变成true，在下个节点到这里碰到了就不在寻找。然后采用队列的先进先出的顺序，把第一个节点的连接的全部放在去，然后依次取出来。这样就把数据遍历到了。也叫 BFS （Breadth-First
Search, BFS）算法。

深度优先搜索DFS：

深度优先搜索（Depth -First Search, DFS）是另一种搜索方法。从顶点 v 出发， D F S按如下过程进行：首先将v 标记为已到达顶点，然后选择一个与 v 邻接的尚未到达的顶点u，如果这样的u 不存在，搜索中止。假设这样的 u 存在，那么从u 又开始一个新的DFS。当从u 开始的搜索结束时，再选择另外一个与v 邻接的尚未到达的顶点，如果这样的顶点不存在，那么搜索终止。而如果存在这样的顶点，又从这个顶点开始 DFS，如此循环下去。

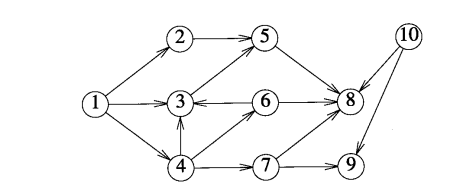
如果v = 1，那么顶点2 , 3和4成为u的候选。假设赋给 u的第一个值是2，到达2的边是( 1 , 2 )，那么从顶点2 开始一次DFS，将顶点2标记为已到达顶点。这时u 的候选只有顶点5，到达5的边是( 2 , 5 )。下面又从 5开始进行DFS，将顶点5标记为已到达顶点，根据边(5.8) 可知顶点8也是可到达顶点，将顶点 8加上标记。从8开始没有可到达的邻接顶点，因此又返回到顶点5，顶点5也没有新的u，因此返回到顶点2，再返回到顶点1。
这时还有两个候选顶点： 3和4。假设选中4，边( 1 , 4 )存在，从顶点 4开始DFS，将顶点 4标记为已到达顶点。现在顶点 3 , 6和7成为候选的u，假设选中6，当u = 6时，顶点 3是唯一的候选，到达3的边是( 6 , 3 )，从3开始D F S，并将3标记为已到达顶点。由于没有与 3邻接的新顶点，因此返回到顶点4，从4开始一个u = 7的DFS，然后到达顶点9，没有与9邻接的其他顶点，这时回到1，没有与1邻接的其他顶点，算法终止。

深度优先搜索：

//深度
template<typename T>
void Graph<T>::DFS()
{
	bool *visited = new bool[n];
	for (int i = 0; i < n; ++i) {
		visited[i] = false;
	}
	for (int j = 0; j < n; ++j) {
		if (!visited[j]) {
			DFS(j, visited);
		}
	}
	delete[] visited;
}

template<typename T>
void Graph<T>::DFS(int v, bool * visited)
{
	visited[v] = true;
	cout << v << " ";
	for (ENode<T> *w = enodes[v]; w; w = w->next) {
		if (!visited[w->adjVex]) {
			DFS(w->adjVex, visited);
		}
	}
}

后面的部分会带大家一起来看看，让这些看起来比较难的，以最简单的方式去理解，需要源码的小伙伴们可以私信我。

比卡丘不皮

关注

2
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
（1小时数据结构）数据结构c++描述（二十五） --- 图（BFS遍历与 DFS遍历）

图的基本概念：简单地说，图（graph）是一个用线或边连接在一起的顶点或节点的集合。如下图：其中a 是无向图，c是有向图。完全图:权和网的含义在某些实际场景中，图中的每条边（或弧）会赋予一个实数来表示一定的含义，这种与边（或弧）相匹配的实数被称为"权"，而带权的图通常称为网。如图 3 所示，就是一个网结构：子图：指的是由图中一部分顶点和边构成的图，称为原图的子图。图的常见存储结构：无向图和有向图最常用的描述方法都是基于邻接的方式：邻接...
复制链接

扫一扫