文章目录
1、买卖股票的最佳时机I&II&III&IV




分析
第一题,
只需要从前往后遍历,一边记录最低价格,一边减去记录的最低价格,然后输出最大差值即可。
第二题,
用到了贪心思想,核心在于“把每天都当成交易日”,也就是遍历一遍,从第二天开始每天都和昨天的价格比较,更大就计入总利润,否则就舍弃。
第三题,
参考:link
这题是二维动态规划问题,存在五种状态:
0、还未开始交易
1、第 1 次买入一支股票
2、第 1 次卖出一支股票
3、第 2 次买入一支股票
4、第 2 次卖出一支股票
它们之间的关系如下:

这里还有个麻烦就是初始化的处理,因为第0天只可能购入一次股票,因此要给 状态3 都赋一个足够小到取不到的值。
因为 dp[i][3] 需从 dp[i-1][3] 中选取 dp[i-1][2]-prices[i] 较大值,如果 dp[0][3] 初始值取0,那么dp[1][3]就会取0(由于这时dp[0][2]==0,所以dp[0][2]-prices[1]等于-prices[1]小于0) ,这时相当于不花钱就购入了股票,显然会导致错误的发生。
代码如下:
int maxProfit(vector<int>& prices) {
int n=prices.size();
if(n==0) return 0;
vector<vector<int>> dp(n,vector<int>(5,0));
dp[0][1]=-prices[0];
dp[0][3]=INT_MIN;
//每种状态只能是从两种状态转变过来,
// 1、什么都不做
// 2、由上一状态转变过来
for(int i=1;i<n;++i){
dp[i][0]=dp[i-1][0];
dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i]);
dp[i][2]=max(dp[i-1][2],dp[i-1][1]+prices[i]);
dp[i][3]=max(dp[i-1][3],dp[i-1][2]-prices[i]);
dp[i][4]=max(dp[i-1][4],dp[i-1][3]+prices[i]);
}
return max(0,max(dp[n-1][2],dp[n-1][4]));
}
复杂度
时间复杂度:O(N)
空间复杂度:O(N)
第四题,
参考:link
首先,要明确一点,如果 k 很大,大到大于等于 len / 2,就相当于股票系列的第 2 题,也即可以进行任何次交易,如下
int greed(vector<int> &prices){
int n=prices.size();
int ret=0;
for(int i=1;i<n;++i){
if(prices[i]-prices[i-1]>0) ret+=(prices[i]-prices[i-1]);
}
return ret;
}
这题的状态要定义为三维:先阶段,即第几天,然后是状态 1,即处在第几个交易,再是状态 2,即现在是持股还是不持股。
这里设持股时状态为1,不持股时状态为0。
dp[i][j][m] :表示到第 i 天为止,已经交易了 j 次,并且当前持股状态为 m 的最大收益。
状态转移方程:
注意,这里要对 j 进行规定,只要当购入股票的时候才将 j 视为进入下一状态。
今天不持股可能由两种情况转移而来,
1)昨天不持股,今天还不持股,说明没有发生新的交易;
2)昨天持股,今天不持股,说明这次交易结束了。这两种情况都在一次交易里。
dp[i][j][0] = max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i])
今天持股同样可能由两种情况转移而来,
1)昨天持股,今天还持股,说明没有发生新的交易,这两天在同一个交易区间里;
2)昨天不持股,今天持股,说明开启了一次新的交易。
dp[i][j][1] = max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i])
初始化:
这里要将所有持股的状态都转为一个足够小的数,道理和第三题一样。
代码如下:
int maxProfit(int k, vector<int>& prices) {
int n=prices.size();
if(k==0||n==0) return 0;
if(k>=n/2) return greed(prices);
vector<vector<vector<int>>> dp(n,vector<vector<int>> (k,vector<int> (2,0)));
for(int i=0;i<n;++i){
for(int j=0;j<k;++j){
if(i==0){
dp[i][j][1]=-prices[0];
}
else{
if(j==0) dp[i][0][1]=max(dp[i-1][0][1],-prices[i]);
else dp[i][j][1]=max(dp[i-1][j][1],dp[i-1][j-1][0]-prices[i]);
dp[i][j][0]=max(dp[i-1][j][0],dp[i-1][j][1]+prices[i]);
}
}
}
return dp[n-1][k-1][0];
}
int greed(vector<int> &prices){
int n=prices.size();
int ret=0;
for(int i=1;i<n;++i){
if(prices[i]-prices[i-1]>0) ret+=(prices[i]-prices[i-1]);
}
return ret;
}
注:因为“只要当购入股票的时候才将 j 视为进入下一状态”这一设定的存在,所以造成一个奇特的现象,即
dp[i][j][0]=max(dp[i-1][j][0],dp[i-1][j][1]+prices[i]);
当 j 等于0时,dp[i][0][0]=max(dp[i-1][0][0],dp[i-1][0][1]+prices[i]),而这里 dp[i][0][1] 是单独讨论的。
所以看上去就是还开始买股票就已经在卖股票了,这是上述状态设定造成的副作用,逻辑上看肯定是有问题的。
但实际上,这里的dp[i][0][0]逻辑上已经是属于第一次交易的售卖阶段了,只有该阶段结束才能进入下一次交易,当然它也会表示尚未进行交易,即一人分饰两角,这里要视max 的结果而定。后面的dp[i][j][0]也存在这个现象。
复杂度
时间复杂度:O(KN)
空间复杂度:O(KN)
2、零钱兑换和完全平方数


分析
找零问题
动态规划的经典题型,本题的状态转移公式如下:
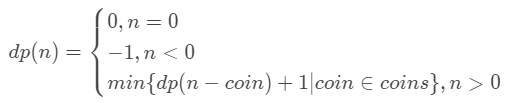
确定base case:目标金额是0的时候,所需的硬币数量是0。
复杂度
时间复杂度:O(kN),k为硬币的数量。
空间复杂度:O(N)
完全平方数
这个和找零属于同类型的题目,状态转移公式也相同,这题可以将平方数理解为硬币,而且是可以不断增长的硬币。
者一开始的想法是将平方数存进一个容器中,然后随着循环的进行不断增长。但这里其实可以用如下手段把这个空间省下来:
dp[1]=1;
for(int i=2;i<n+1;++i){
int min_squ=INT_MAX;
for(int j=1;i-j*j>=0;++j){
if(dp[i-j*j]!=-1){
min_squ=min(min_squ,dp[i-j*j]+1);
}
}
if(min_squ!=INT_MAX) dp[i]=min_squ;
else dp[i]=-1;
}
复杂度
时间复杂度:O(kN),k为平方数的数量,这是个不断增长的值
空间复杂度:O(N)
3、丑数 I&II
题目
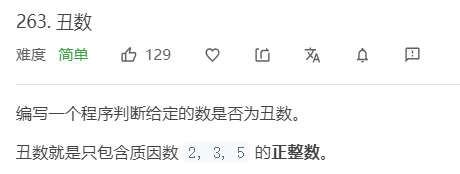

分析
第一题只需要检查给的数能否整除2,3,5,能就整除,不能返回false。直到等于1时返回true。
第二题有优先队列和动态规划两种方法:
优先队列:利用优先队列有自动排序的功能,每次取出队头元素,存入队头元素2、队头元素3、队头元素*5。
注:像12这个元素,可由4乘3得到,也可由6乘2得到,要做去重处理(哈希表);
动态规划:参考下面过程
1打头,1乘2 1乘3 1乘5,现在是{1,2,3,5}
轮到2,2乘2 2乘3 2乘5,现在是{1,2,3,4,5,6,10}
这里维护一个n长度的数组,第一个位置的值定义为1,然后再维护三个指针p2,p3,p5三个指针,指向首位。
每次循环让他们分别乘以2,3,5并取其最小的值作为 i 的值,并将对应的指针+1。
这里需要理解到,每个位置的数 i 最多只能乘一次2,3,5,如1乘2后得到第二个位置的值2,这时++p2,那么1在后面只能够乘以3或5了。
还要这里也要注意去重的问题,要做如下处理:
int num=min(dp[p2]*2,min(dp[p3]*3,dp[p5]*5));
if(num==dp[p2]*2) ++p2;
if(num==dp[p3]*3) ++p3;
if(num==dp[p5]*5) ++p5;
复杂度
时间复杂度:O(N)
空间复杂度:O(N)
4、最长回文子串
题目

分析
本题是经典的DP题,状态转移公式是
if(s[i]==s[j]){
dp[i][j]=dp[i+1][j-1]+2
}
这里需要注意的一点在于循环的先后顺序,因为这里使用的是自下而上的思路,所以循环应该如下:
for(int i=1;i<n;++i){
for(int j=0;j<i;++j){
if(s[i]==s[j]){
if(i==j+1) dp[j][i]=2;
dp[j][i]=(dp[j+1][i-1]==-1)?-1:(dp[j+1][i-1]+2);
if(max_len!=max(max_len,dp[j][i])){
max_len=max(max_len,dp[j][i]);
start=j;
}
}
else dp[j][i]=-1;
}
}
这里是先将i之前的所有dp信息得到再进入i+1,之所以这样做,原因如下:
如果循环使用下面这种模式
for(int i=0;i<n;++i){
for(int j=i;j<n;++j){
}
}
当遇到“aaaa”时,最大长度是dp[0][3],它是基于dp[1][2]的,但在i等于0循环结束前都不会去对i=1进行循环,所以此时dp[1][2]仍然是初始值,就会导致错误发生。
复杂度
时间复杂度:O(N^2)
空间复杂度:O(N^2)
5、最大子序、最长上升子序列


分析
最大序列和:
这道题要维护一个前面i-1个数的最大和sum,然后到i的时候,如果sum大于0则更新sum为sum+nums[i]。否则令sum为nums[i]。
int sum=nums[0],maxsum=nums[0];
for(int i=1;i<nums.size();++i){
if(sum>0) sum+=nums[i];
else sum=nums[i];
maxsum=max(sum,maxsum);
}
复杂度
时间复杂度:O(N)
空间复杂度:O(1)
最长上升子序列:
这题关键是要确定好DP的状态,首先考虑将子序列的长度定义为状态,但这么做的话,状态转移就有些犯难了。
这里考虑
将dp[i] 表示以 nums[i] 结尾的「上升子序列」的长度。
这样在谈论i的时候只用把nums[i]同i之前的所有数找一遍,只要 nums[i] 严格大于在它位置之前的某个数,那么 nums[i] 就可以接在这个数后面形成一个更长的上升子序列。因此,dp[i] 就等于下标 i 之前严格小于 nums[i] 的状态值的最大者 +1。
状态转移公式如下:
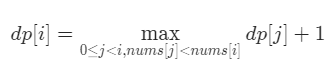
注意,这里dp[i]的值应当大于等于1。
vector<int> dp(n,0);
dp[0]=1;
int maxlen=0;
for(int i=1;i<n;++i){
int len=1;
for(int j=0;j<i;++j){
if(nums[j]<nums[i]) len=max(len,dp[j]+1);
}
dp[i]=len;
maxlen=max(maxlen,len);
}
时间优化,参考:link
这里将时间由O(N^2)降到了O(NlgN),首先定义新的状态,
我们考虑维护一个列表 dp,其中每个元素dp[k] 的值代表 长度为 k+1 的子序列尾部元素的值。
如[1,4,6] 序列,长度为 1,2,3的子序列尾部元素值分别为 dp= [1,4,6]
状态转移公式:
在遍历计算每个 dp[k],不断更新长度为[1,k]的子序列尾部元素值,始终保持每个尾部元素值最小(例如[1,5,3],遍历到元素5时,长度为2的子序列尾部元素值为5;当遍历到元素3时,尾部元素值应更新至3。)
这里得到的dp数组是个递增数组,因此可以使用二分法查找当前数应该在dp数组中的位置。

代码如下:
int lengthOfLIS(vector<int>& nums) {
int n=nums.size();
if(n<2) return n;
vector<int> dp(n,0);
dp[0]=nums[0];
int res=0;
for(int i=1;i<n;++i){
if(nums[i]>dp[res]){
++res;
dp[res]=nums[i];
}
else{
int left=0,right=res;
while(left<right){
int mid=left+((right-left)>>1);
if(dp[mid]>=nums[i]) right=mid;
else left=mid+1;
}
if(dp[right]>nums[i]) dp[right]=nums[i];
}
}
return res+1;
}
复杂度
时间复杂度:O(N^2)及 O(NlgN)
空间复杂度:O(N)
6、单词拆分
题目

分析
这题的状态其实是很明显的,dp[i]表示i之前的字符串能否拆分。
状态转移公式:
这题的状态转移公式有点难顶,首先检查到i为止的子字符串是否在字典中,如果在就将dp[i]置为true。
如果不在就从0到i进行遍历,检查是否存在“dp[j]=true”+“j到i的子字符串也在字典中”,如果存在就将dp[i]置为true。
如下:
for(int i=0;i<n;++i){
if(us.count(s.substr(0,i+1))) dp[i]=1;
else{
for(int j=0;j<i;++j){
if(dp[j]&&us.count(s.substr(j+1,i-j))){
dp[i]=1;
break;
}
}
}
}
注:这里为快速检查,可以将字典中的字符串存在哈希表中。
结果:
考察dp[n-1]是否为true。
复杂度
时间复杂度:O(N^2)
空间复杂度:O(N)
7、最小路径和
题目

分析
这里状态很明确,就是走到[i,j]位置的最小路径和。
状态转移:
由于只能向下或向右移动,所以
dp[i][j]=grid[i][j]+min(dp[i][j-1],dp[i-1][j]);
这里还应该注意在最上一排和最左一排只有dp[i][j-1]或dp[i-1][j]中的一种情况,如下:
dp[0][0]=grid[0][0];
for(int i=0;i,i<row;++i){
for(int j=0;j<col;++j){
if(i==0&&j==0) continue;
if(i==0) dp[i][j]=grid[i][j]+dp[i][j-1];
else if(j==0) dp[i][j]=grid[i][j]+dp[i-1][j];
else{
dp[i][j]=grid[i][j]+min(dp[i][j-1],dp[i-1][j]);
}
}
}
初始化:
这里为防止越界,dp[0][0]=grid[0][0];然后在遍历中将它略过。
复杂度
时间复杂度:O(N^2),N为边数
空间复杂度:O(N^2)
8、买卖股票带冷却期&带手续费


分析
参考了力扣liweiwei1419的解答。
这两题的状态转移中都涉及了内部切换,所以DP数组应该设计成二维数组。
含手续费
状态分为持股、不持股两种。
初始化:不持股时为0,持股是为-prices[0]
状态转移方程:
状态为 i 时,有持股、不持股两种情况。
持股,可能是有 i-1 不持股买股票得到,也可能是 i-1 持股不变得到。
不持股,可能是 i-1 持股卖股票得到,也可能是 i-1 不持股不变得到。
如下:
for(int i=1;i<n;++i){
dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i]-fee);
dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i]);
}
含冷却期
状态分为持股、不持股和冷却期三种。
初始化:不持股和冷却期时为0,持股是为-prices[0]
状态转移方程:
不持股可由不持股和持股卖掉转换过来。
持股可由持股和冷冻期买股票转换过来。
因为股票卖掉后进入一天冷冻期,卖掉股票后就已经进入不持股的状态,所以冷冻期只能由不持股转换过来,冷冻期都是由前一天卖掉股票后转换过来的,这里不存在保持不变。
如下图所示:

注意:返回值取最后一天在冷却期和不持股状态中的较大值。
优化
这里两种方案都有优化的空间,因为这两题的解法都是在参考昨天的值,所以不必设 n 阶的dp数组。
这里有个技巧就是使用滚动数组,以冷却期举例:
vector<vector<int>> dp(2,vector<int>(3,0));
//0 表示不持股;
dp[0][0]=0;
//1 表示持股;
dp[0][1]=-prices[0];
//2 表示处在冷冻期。
dp[0][2]=0;
for(int i=1;i<n;++i){
dp[i&1][0]=max(dp[(i-1)&1][0],dp[(i-1)&1][1]+prices[i]);
dp[i&1][1]=max(dp[(i-1)&1][1],dp[(i-1)&1][2]-prices[i]);
dp[i&1][2]=dp[(i-1)&1][0];
}
return max(dp[(n-1)&1][0],dp[(n-1)&1][2]);
这里注意返回值取 (n-1)&1 。
复杂度
时间复杂度:O(N)
空间复杂度:O(1)
9、零钱兑换II
题目

分析
解答参考了link
实话实说,本题难度和 零钱兑换I 不可同日而语,而且就目前来看,这题似乎更受欢迎。
注意,零钱兑换I 中的方法无法套用到这里来,因为会出现重复。比如这里的“2+2+1”和“1+2+2”。
状态转移公式:
首先,这里使用两位数组 dp[i][j] 表示硬币列表的前缀子区间 [0, i] 能够凑成总金额 j 的组合数。转移公式如下:
dp[i][j] = dp[i - 1][j - 0 * coins[i]] +
dp[i - 1][j - 1 * coins[i]] +
dp[i - 1][j - 2 * coins[i]] +
... +
dp[i - 1][j - k * coins[i]];
其中,j - k * coins[i] >= 0。
对于遍历到第 i 枚硬币时,按0枚、1枚、2枚……k枚的往 i-1 枚硬币的总金额上添加,看是否能凑够金额 j 。
这里每添加一个硬币就把它可能的情况全部遍历到,后面也不会再用到它,因此不用担心重复的问题。
整体如下:
for(int i=1;i<n;++i){
for(int j=0;j<amount+1;++j){
int k=0;
while(j-k*coins[i]>=0){
dp[i][j]+=dp[i-1][j-k*coins[i]];
++k;
}
}
}
初始化:
这里需要注意的是 dp[0][0] 应该等于 1 。原因是当 dp[i - 1][j - k * coins[i]] 的第 2 个坐标 j - k * coins[i] == 0 成立的时候,k 个硬币 coin[i] 就恰好成为了一种组合。
然后再将第一行填写完毕,如下:
dp[0][0]=1;
for(int j=coins[0];j<amount+1;j+=coins[0]){
dp[0][j]=1;
}
复杂度
时间复杂度:O(NM^2),这里金额为 M,硬币数为 N。
空间复杂度:O(NM),表格有 N 行,M 列。
时间优化
在上述解的基础上,经过无穷级数的运算可以得到如下状态转移方程:
dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i]]
改正后如下:
for(int i=1;i<n;++i){
for(int j=0;j<amount+1;++j){
dp[i][j]=dp[i-1][j];
if(j-coins[i]>=0){
dp[i][j]+=dp[i][j-coins[i]];
}
}
}
空间优化
这里基于当前状态行的值,只和上一行的状态值相关。
这里要注意,因为会刷新 i-1 的数据,所以应该从小往大遍历。如下:
vector<int> dp(amount+1,0);
dp[0]=1;
//初始化第一行
for(int j=coins[0];j<amount+1;j+=coins[0]){
dp[j]=1;
}
for(int i=1;i<n;++i){
for(int j=coins[i];j<amount+1;++j){
dp[j]+=dp[j-coins[i]];
}
}
复杂度
时间复杂度:O(NM),这里金额为 M,硬币数为 N。
空间复杂度:O(M)
10、打家劫舍II&III


分析
II
因为这里II是完全基于I的基础之上,所以这里只讨论II。
II与I不同的点和难点在于第一家和最后一家只能打劫一家,所以这里分开进行讨论。
只打劫第一家:
vector<vector<int>> dp(n,vector<int>(2,0));
dp[1][1]=nums[1];
int max_rob=0;
for(int i=2;i<n;++i){
dp[i][0]=max(dp[i-1][0],dp[i-1][1]);
dp[i][1]=dp[i-1][0]+nums[i];
}
max_rob=max(dp[n-1][0],dp[n-1][1]);
只打劫最后一家:
dp[0][1]=nums[0];
for(int i=1;i<n-1;++i){
dp[i][0]=max(dp[i-1][0],dp[i-1][1]);
dp[i][1]=dp[i-1][0]+nums[i];
}
max_rob=max(max_rob,max(dp[n-2][0],dp[n-2][1]));
从两者中取较大值即可。
显然,这里第i天的值只基于前一天,所以在空间上可以进行优化,如下:
int max_rob=0;
int dp0=0,dp1=nums[1];
for(int i=2;i<n;++i){
int a=dp0,b=dp1;
dp0=max(a,b);
dp1=a+nums[i];
}
max_rob=max(dp0,dp1);
dp0=0;dp1=nums[0];
for(int i=1;i<n-1;++i){
int a=dp0,b=dp1;
dp0=max(a,b);
dp1=a+nums[i];
}
max_rob=max(max_rob,max(dp0,dp1));
复杂度
时间复杂度:O(N)
空间复杂度:O(1)
III
这里的三属于树类的DP问题,要配合着DFS来做才行。
这里使用了后序遍历,然后让子结点陆续汇报信息给父结点,一层一层向上汇报,最后在根结点汇总值。
状态转移公式:
这里的状态定义应该为 dp[node][i] 其中node表示树的结点,而 i 只能取 0 和 1 ,分别表示打劫与不打劫。
但是这里node几乎是无法实现的,所以我们只留下 i ,然后依靠递归进行状态转移,代码如下:
int rob(TreeNode* root) {
if(root==NULL) return 0;
vector<int> ret;
ret=dfs(root);
return max(ret[0],ret[1]);
}
vector<int> dfs(TreeNode* root){
if(root==NULL) return {0,0};
vector<int> l=dfs(root->left);
vector<int> r=dfs(root->right);
vector<int> ret(2,0);
ret[0]=max(l[0],l[1])+max(r[0],r[1]);
ret[1]=l[0]+r[0]+root->val;
return ret;
}
复杂度
时间复杂度:O(NlgN),这里要把整个树遍历一遍
空间复杂度:O(NlgN)
11、编辑距离
题目

分析
参考了:link
这题的状态转移确实有点难想出来,具体如下:
状态转移公式:
dp[i][j] 代表 word1 到 i 位置转换成 word2 到 j 位置需要最少步数。
当 word1[i] == word2[j],dp[i][j] = dp[i-1][j-1];
当 word1[i] != word2[j],dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1;
其中,dp[i-1][j-1] 表示替换操作,dp[i-1][j] 表示删除操作,dp[i][j-1] 表示插入操作。
初始化:
这里的初始情况如下图所示:

其中:
第一行,是 word1 为空变成 word2 最少步数,就是插入操作。
第一列,是 word2 为空,需要的最少步数,就是删除操作。
代码如下:
vector<vector<int>> dp(n1+1,vector<int>(n2+1,0));
for(int i=1;i<n1+1;++i) dp[i][0]=i;
for(int j=1;j<n2+1;++j) dp[0][j]=j;
for(int i=1;i<n1+1;++i){
for(int j=1;j<n2+1;++j){
if(word1[i-1]==word2[j-1]) dp[i][j]=dp[i-1][j-1];
else dp[i][j]=min(dp[i-1][j-1],min(dp[i][j-1],dp[i-1][j]))+1;
}
}
注意:这里word1和word2在循环时应该是i-1和j-1。
复杂度
时间复杂度:O(MN),其中M,N分别为word1和word2的长度。
空间复杂度:O(MN)
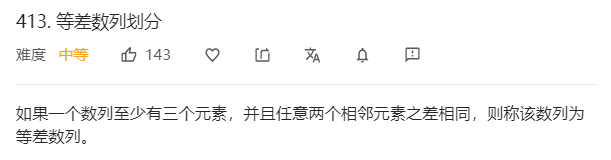
12、区域和检索 - 数组不可变& 等差数列划分


分析
这两题都属于数组区间型DP问题。
区域和检索 - 数组不可变
状态转移:
令dp[i] 为前 i 个值的和,如此 i 与 j 之间的和就是 dp[j] - dp[i-1] 。
复杂度
时间复杂度:O(N)
空间复杂度:O(N)
等差数列划分
本题的难度也在于状态难以确认,开始的想法是最朴素的让dp[i] 表示前 i 个数的所有为等差数组的子数组个数,但这样做后的状态转移实在想不出。
状态转移:
令dp[i] 为以 A[i] 为结尾的等差递增子区间的个数。
当 A[i] - A[i-1] == A[i-1] - A[i-2],那么 [A[i-2], A[i-1], A[i]] 构成一个等差递增子区间。而且在以 A[i-1] 为结尾的递增子区间的后面再加上一个 A[i],一样可以构成新的递增子区间,同时还多了一个 { A[i-2] , A[i-1] , A[i] } 。如下所示
dp[2] = 1
[0, 1, 2]
dp[3] = dp[2] + 1 = 2
[0, 1, 2, 3], // [0, 1, 2] 之后加一个 3
[1, 2, 3] // 新的递增子区间
dp[4] = dp[3] + 1 = 3
[0, 1, 2, 3, 4], // [0, 1, 2, 3] 之后加一个 4
[1, 2, 3, 4], // [1, 2, 3] 之后加一个 4
[2, 3, 4] // 新的递增子区间
因为题目求的是子序列的总和,所以最后需要返回 dp 数组累加的结果。
代码如下:
vector<int> dp(n,0);
int ret=0;
for(int i=2;i<n;++i){
if(A[i]-A[i-1]==A[i-1]-A[i-2]) dp[i]=dp[i-1]+1;
ret+=dp[i];
}
复杂度
时间复杂度:O(N)
空间复杂度:O(N)
13、乘积最大子数组
题目

分析
这题的和最大和的子数组差不多的思路,但是这里有个需要注意的地方,就是遇到负数的时候,最小值和最大值乘以了负数后地位会互换。因此这里要维护一个最大值 imax 和最小值 imin ,当遇到负数时互换它们的值。代码如下:
int maxProduct(vector<int>& nums) {
int n=nums.size();
int imin=1,imax=1,maxnum=INT_MIN;
for(int i=0;i<n;++i){
if(nums[i]<0){
swap(imin,imax);
}
imax=max(imax*nums[i],nums[i]);
imin=min(imin*nums[i],nums[i]);
maxnum=max(maxnum,imax);
}
return maxnum;
}
复杂度
时间复杂度:O(N)
空间复杂度:O(1)
14、地下城游戏
题目

分析
参考:link
这题审题要严一些,这里要求的并不是哪条路径到终点后生命最高,而是所需生命最低,如例子中如果走:下->下->右->右 这条路线的话,要进到10的格子前必须要有8点生命值才行。
参考中提出了带备忘录的DFS+回溯做法,也即尝试每条路。
后面给出了动态规划的做法,这里需要从终点往起点移动,然后用dp记录进入每个格子前至少需要多少条命,如例子中进入终点前需要6条命(这里做的时候还是记为5,然后在输出时加一)。
这里需要注意的是,dp的值需要大于0,这是当然的,不然你进入前是负的岂不是已经shi了。
代码如下:
int calculateMinimumHP(vector<vector<int>>& dungeon) {
int row=dungeon.size();
int col=dungeon[0].size();
vector<vector<int>> dp(row,vector<int> (col,0));
int minnum=0;
dp[row-1][col-1]=max(-dungeon[row-1][col-1],0);
for(int i=row-1;i>=0;--i){
for(int j=col-1;j>=0;--j){
if(i==row-1&&j==col-1) continue;
if(i==row-1) minnum=dp[i][j+1]-dungeon[i][j];
else if(j==col-1) minnum=dp[i+1][j]-dungeon[i][j];
else minnum=min(dp[i][j+1],dp[i+1][j])-dungeon[i][j];
dp[i][j]=max(minnum,0);
}
}
return dp[0][0]+1;
}
注意:最后的 dp[i][j]=max(minnum,0) 这步操作,是因为如上所说的,在进格子前生命值不能低于0。
复杂度
时间复杂度:O(N^2)
空间复杂度:O(N^2)
15、分割等和子集
题目

分析
参考:link
这题属于0-1背包问题,可以看做是零钱兑换的不可重复使用版本,这里的目标数是数组和的一半。
状态转移:
dp[i][j]表示从数组的 [0, i] 这个子区间内挑选一些正整数,每个数只能用一次,使得这些数的和恰好等于 j 。

初始化:
if (nums[0] <= target) {
dp[0][nums[0]] = 1;
}
因为一个数只能用一次,因此这里只将 dp[0][nums[0]] 置 1 。
代码如下:
bool canPartition(vector<int>& nums) {
int n = nums.size();
int sum = accumulate(nums.begin(), nums.end(), 0);
//如果数组和为奇数,则无法等分为两部分
if (n<2||sum % 2) return false;
vector<vector<int>> dp(n, vector<int>(sum / 2 + 1, 0));
if (nums[0] <= target) {
dp[0][nums[0]] = 1;
}
for (int i = 1; i < n; ++i) {
for (int j = 1; j <= sum / 2; ++j) {
if (dp[i - 1][j]) dp[i][j] = 1;
else if (j == nums[i]) dp[i][j] = 1;
else if (j > nums[i]) dp[i][j] = dp[i - 1][j - nums[i]];
}
}
return dp[n - 1][sum / 2];
}
复杂度
时间复杂度:O(NC):这里 N 是数组元素的个数,C 是数组元素的和的一半。
空间复杂度:O(NC)
16、最长公共子序列
题目

分析
参考:link
本题亦属于经典的DP问题。
对于两个字符串,一般需要构造出如下的状态表:

状态转移公式:
其中,dp[i][j] 表示对于 s1[1…i] 和 s2[1…j],它们的 LCS (最长公共子序列)长度是 dp[i][j]。
当 s1[i]==s2[j] 时 dp[i][j]=dp[i-1][j-1]+1
否则,dp[i][j]取dp[i-1][j] 和 dp[i][j-1] 中大的那个(注意,dp[i-1][j-1]是恒小于等于dp[i-1][j] 和 dp[i][j-1]的)。
初始化:
这里一般要设的比字符串多一格,然后以第 0 格来表示空字符。
由于长度为0的空子串不可能和任何子串有LCS,所以dp[0][…] 和 dp[…][0] 都应该初始化为 0。
代码如下:
int longestCommonSubsequence(string text1, string text2) {
int n1=text1.size(),n2=text2.size();
if(n1==0||n2==0) return 0;
vector<vector<int>> dp(n1+1,vector<int>(n2+1,0));
for(int i=1;i<=n1;++i){
for(int j=1;j<=n2;++j){
if(text1[i-1]==text2[j-1]) dp[i][j]=dp[i-1][j-1]+1;
else dp[i][j]=max(dp[i][j-1],dp[i-1][j]);
}
}
return dp[n1][n2];
}
复杂度
时间复杂度:O(N^2)
空间复杂度:O(N^2)
17、三角形最小路径和
题目

分析
参考:link
这题从底层往顶推要更简单些,由题意可得状态转移公式如下,
f(i,j)=min(f(i+1,j),f(i+1,j+1))+triangle[i][j]
代码如下:
int minimumTotal(vector<vector<int>>& triangle) {
int n=triangle.size();
if(n==0) return 0;
vector<vector<int>> dp(n+1,vector<int>(n+1,0));
for(int i=n-1;i>=0;--i){
for(int j=0;j<=i;++j){
dp[i][j]=min(dp[i+1][j],dp[i+1][j+1])+triangle[i][j];
}
}
return dp[0][0];
}
注:因为这里所以为了方便,将dp设为 n+1 然后从n-1开始,这时第 n 层全是0,所以第 n-1层就是triangle 的第n-1 层。省去了专门初始化第 n-1 的步骤。
复杂度
时间复杂度:O(N^2),其中N为三角形的层数
空间复杂度:O(N^2)
18、鸡蛋掉落
题目

分析
特例:两个鸡蛋,100层楼的解答,见link
参考:link
这题难度颇大,堪比正则表达式匹配,也是经典的DP做法。
状态转移公式:
dp[i][j]:一共有 j 层楼梯的情况下,使用 i 个鸡蛋的最少实验的次数
注:这里状态没和参考中设的一样,因为我还是习惯在两层的for循环中外层放两维矩阵的第一维度。
当我们从楼层k(k>=1&&k<=j)丢鸡蛋时,会有两种情况:
①鸡蛋破摔,则测试 F 值的实验就得在 k 层以下做(不包括 k 层),这里已经使用了一个鸡蛋,因此测出 F 值的最少实验次数是:dp[i-1][k-1];
②鸡蛋完好,测试 F 值的实验就得在 k 层以上做(不包括 k 层),这里这个鸡蛋还能使用,因此测出 F 值的最少实验次数是:dp[i][j-k]。如总共 8 层,在第 5 层扔下去没有破碎,则需要在 [6, 7, 8] 层继续做实验,因此区间的大小就是 8 - 5 = 3。
最坏情况下,是这两个子问题的较大者,由于在第 k 层扔下鸡蛋算作一次实验,k 的值在 1≤k≤i,对于每一个 k 都对应了一组值的最大值,最后取这些 k 下的最小值(最优子结构)作为dp[i][j]的值。
代码如下:
int superEggDrop(int K, int N) {
//dp[i][j]:一共有 j 层楼梯的情况下,使用 i 个鸡蛋的最少实验的次数
vector<vector<int>> dp(K+1,vector<int>(N+1,0));
//只有一层楼时,鸡蛋数大于0时都只需尝试一次
for(int i=1;i<=K;++i) dp[i][1]=1;
//只有一个鸡蛋时,楼层数大于0时在最差情况下需要尝试与楼层数相等的次数
for(int j=1;j<=N;++j) dp[1][j]=j;
for(int i=2;i<=K;++i){
for(int j=2;j<=N;++j){
int mintimes=N;
for(int k=1;k<=j;++k){
mintimes=min(mintimes,max(dp[i-1][k-1],dp[i][j-k])+1);
}
dp[i][j]=mintimes;
}
}
return dp[K][N];
}
但这个算法的时间复杂度达到了惊人的O(KN^2),因为使用三层 for 循环,每层循环都是线性的;
这里观察dp[i-1][k-1]和dp[i][j-k]可知,它们一个的值随k值的增大而增大,另一个随k值的增大而减小,具体见参考中的配图。结论如下,
二者的较大值的最小点在它们交汇的地方。那么有没有可能不交汇,当然有可能(上面第 3 张图),二者较大值的最小者一定出现在画成曲线段交点的两侧,并且二者的差值不会超过 11,也就是如果没有重合的点,两边的最大值是一样的(从图上看出来的,没有严格证明),因此取左侧和右侧两点中的一点都可以,不失一般性,可以取左边的那个点的 k。
因此我们可以用二分法对上述做法进行改进,代码如下:
int superEggDrop(int K, int N) {
//dp[i][j]:一共有 j 层楼梯的情况下,使用 i 个鸡蛋的最少实验的次数
vector<vector<int>> dp(K+1,vector<int>(N+1,0));
//只有一层楼时,鸡蛋数大于0时都只需尝试一次
for(int i=1;i<=K;++i) dp[i][1]=1;
//只有一个鸡蛋时,楼层数大于0时在最差情况下需要尝试与楼层数相等的次数
for(int j=1;j<=N;++j) dp[1][j]=j;
for(int i=2;i<=K;++i){
for(int j=2;j<=N;++j){
int left=1,right=j;
while(left<right){
int mid=left+((right-left+1)>>1);
if(dp[i-1][mid-1]>dp[i][j-mid]) right=mid-1;
else left=mid;
}
dp[i][j]=max(dp[i-1][left-1],dp[i][j-left])+1;
}
}
return dp[K][N];
}
复杂度
时间复杂度:O(NK*lgN)
空间复杂度:O(NK)






















 5260
5260











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








