均值定理四个公式_柯西-古萨定理

定理1 (古萨定理). 设

是

中的一个开集,

是一个三角形并且它的内部也包含于

, 那么

其中

是

中的全纯函数.

证明. 将初始的三角形记作

(它具有固定的定向, 这里我们选正定向), 它的直径和周长并分别记作

和

. 证明的第一步是将该三角形的每一边二等分并将中点连起来. 这样就得到四个与原三角形相似的小三角形, 记作

和

. 构造的过程以及每个小三角形的定向如图1所示. 定向的选择与原三角形一致, 因此, 将沿同一边不同方向的积分抵消之后, 我们得到

(1)

对某个

必然有

否则的话将与(1)矛盾. 选取一个满足这一不等式的三角形, 并将它重命名为

. 注意, 如果

和

分别表示

的直径和周长, 那么

并且

. 现在我们对三角形

重复这一过程, 将它对分为更小的四个三角形. 继续这一过程, 我们将得到一系列三角形

它们满足性质

和

其中

和

分别表示

的直径和周长. 用

表示以

为边界的实心闭三角形, 并注意到我们的构造过程产生了一嵌套紧致序列

它的直径趋于

. 根据闭区间套定理的二维推广, 存在唯一点

使得它属于每一个实心三角形

. 由于

在点

是全纯的, 我们可以将它写成

其中当

时

. 由于常数

和线性函数

具有原函数, 因此它们沿闭曲线

的积分为零, 这样的话将上面的等式积分得到

(2)

现在

属于实心三角形

的闭包并且

属于它的边界, 所以必然有

, 利用(2)就得到估计

其中当

时

. 因此

由此得到我们的最终估计

令

, 考虑到

, 定理的证明就完成了.

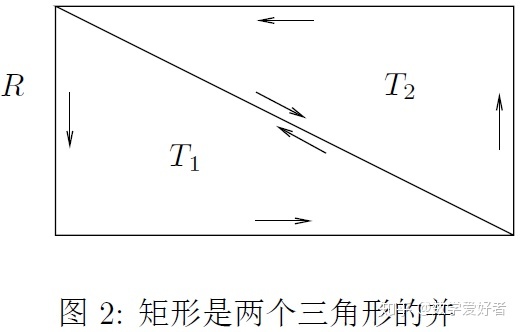
推论2. 设

是开集

内的全纯函数, 并且该开集包含矩形

及其内部, 则

证明. 这是显然的. 我们选取一个如图2所示的定向并注意到

定理3(原函数的局部存在性). 一个开圆盘内的全纯函数在那个圆盘内有原函数.

证明. 通过平移, 不失一般性我们可以假设该圆盘, 譬如说

, 中心位于原点. 给定一点

, 先沿水平方向由

运动到

, 然后竖直方向由

运动到

将得到一条分段光滑曲线. 选择由

到

的定向并将该折线记作

(它最多包含两条线段), 如图3所示.

定义

从

的选择可以看出函数

的定义是明确的. 我们断言

是

内的全纯函数并且

. 为了证明这一结论, 固定

并选取充分小的

使得

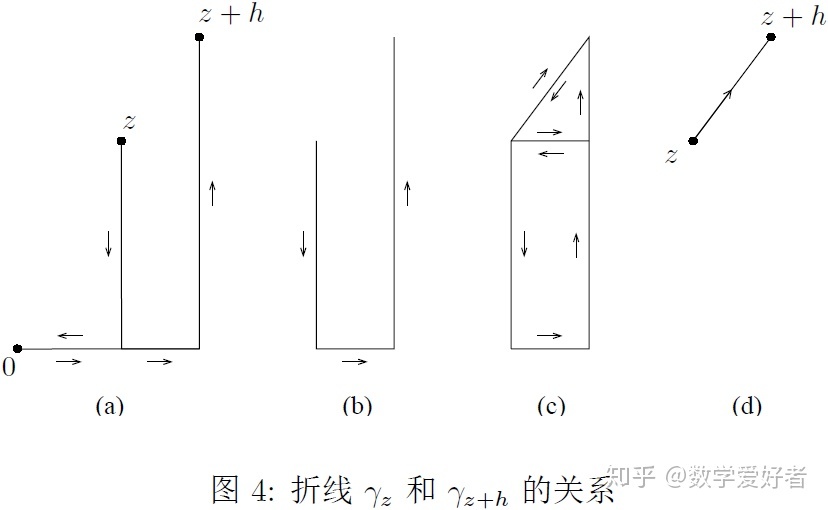
也属于该圆盘. 现在考虑差分

函数

首先沿

的原始定向积分, 然后沿

的反向积分(因为第二个积分前面有个负号). 这对应于图4中的(a). 由于我们将

沿连接原点的线段的两个不同方向积分, 它们相互抵消, 因此剩下(b)中的轮廓. 然后, 如图(c)所示那样补全矩形和三角形, 之后利用关于三角形和矩形的古萨定理就剩下(d)中所示的由

到

的直线段.

因此通过上面的对消我们得到

其中

是连接

和

的直线段. 由于

在

点连续, 我们有

其中当

时

. 因此

(3)

一方面, 常数

具有原函数

, 所以第一个积分就是

. 另一方面, 我们有如下估计:

当

趋于

时, 上式中的上界也趋于零, 因此由(3)我们得到

这就证明了在该圆盘内

是

的原函数.

定理4 (圆盘的柯西定理). 设

是某圆盘内的全纯函数, 则对于该圆盘内的任意闭曲线

有

证明. 因为

在该圆盘内有原函数.

定理5(柯西积分公式). 假设

是某个开集内的全纯函数, 该开集包含圆盘

的闭包. 若

表示圆盘

的边界且具有正的定向, 则

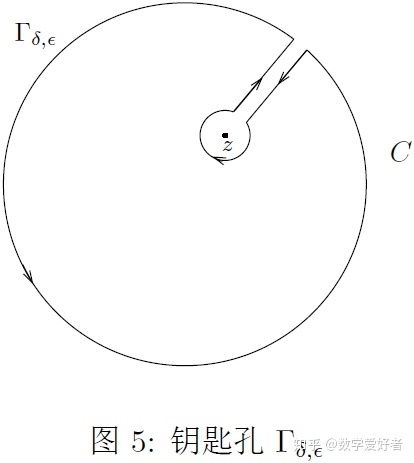
证明. 固定

并考虑如图5所示挖掉

点的``钥匙孔''

.

这里

是狭缝的宽度, 而

是中心位于

点的小圆的半径. 由于函数

在除点

以外的其它地方是全纯的, 因此, 根据关于简单轮廓(toy contour)的柯西定理有

现在, 通过令

趋于

使得狭缝变得更窄, 然后利用

的连续性我们看到, 在极限的情况下狭缝两边上的积分相互抵消. 剩下的部分由两个圆构成, 其中大的边界圆

具有正的定向, 而中心位于

半径为

的小圆

具有负的定向, 即顺时针. 为了了解这个小圆上积分的具体情况, 我们将

写成

(4)

并注意到由于

是全纯的, 所以(4)式右边的第一项是有界的, 因此当

时它在

上的积分趋于

. 为了完成证明, 我们只需注意到

所以在极限的情况下我们发现

如所求.

推论6. 若

是某个开集

内的全纯函数, 那么

在

内具有无穷阶复导数. 此外, 若

是一个圆并且它的内部也包含于

, 则

对所有位于

内部的点

成立.

证明. 对

进行归纳,

的情形就是柯西积分公式. 假设

具有直到

阶的复导数并且

现在, 对于小的

,

的差商具有如下形式

(5)

回忆

令

以及

, 我们看到式(5)括号中的项等于

注意到若

很小, 则

和

离边界圆

具有有限的距离, 因此在

趋于

的极限情况下, 我们发现上面的差商收敛到

这就完成了归纳法的论证从而证明了定理.

推论7(柯西不等式). 若

是某个开集内的全纯函数, 并且该开集包含中心位于

半径为

的圆盘

的闭包, 则

其中

表示

在边界圆

上的上确界.

证明. 对

应用柯西积分公式得到

定理8. 假设

是某个开集

内的全纯函数. 若

是中心位于

的圆盘并且它的闭包包含于

, 那么对所有

,

在

处有级数展开

并且系数由下式给出:

证明. 固定

. 由柯西积分公式我们有

(6)

其中

表示圆盘的边界并且

. 我们的想法是将

写成

（7）

并利用几何级数展开. 由于

并且

固定, 因此存在

使得

于是

(8)

并且该级数对

一致收敛. 这使得我们可以交换无穷和以及积分号的次序, 结合(6), (7)和(8)得到

这就完成了级数展开的证明. 此外, 利用关于导数的柯西积分公式就证明了

的公式.

推论9 (刘维尔定理). 若

是整函数并且是有界的, 则

是常数.

证明. 由于

是连通的, 因此只需证明

即可.

对每一个

以及所有

, 柯西不等式蕴含

其中

是

的一个界. 令

就得到所需的结论.

推论10 (代数基本定理). 每一个具有复系数的非常值多项式

在

中有根.

证明. 若

没有根, 则

是有界的全纯函数. 要了解这一点, 我们当然可以假设

, 那么当

时有

当

时括号中的项趋于

, 所以我们断定存在

使得若

, 则

特别地, 当

时

有下界. 由于

是连续的并且在圆盘

中无根, 因此它在该圆盘中也有下界, 这就证明了我们的断言.

根据刘维尔定理我们得出结论,

是常数. 这与我们的假设

非常值矛盾, 这就完成了推论的证明.

推论11(代数基本定理). 每一个阶

的多项式

在

中恰好有

个根. 若把这些根记作

, 则

可以分解为

证明. 根据前面的结论

有一个根, 譬如说

. 将

写成

并代入

, 然后利用二项公式我们得到

其中

是新的系数, 并且

. 由于

, 我们发现

, 因此

其中

是

阶多项式. 通过对多项式的阶进行归纳, 我们得出结论,

有

个根并且对某个

可以表示成

将右侧展开我们发现

的系数是

, 因此

.

定理12. 假设

是区域

中的全纯函数并且对于一列极限点位于

的不同点序列退化, 则

恒等于

.

证明. 假设

是序列

的一个极限点并且

. 首先我们证明

在包含

的一个小圆盘内恒等于零. 为此, 我们选取一中心位于

并且包含于

的圆盘, 并考虑

在该圆盘内的幂级数展开

若

不恒等于零, 则存在一个最小的整数

使得

. 但这样的话

可以写成

其中当

时

收敛到

. 取

为一列收敛到

的点, 我们就得出矛盾, 因为

并且

, 但是

.

我们利用

连通这一事实来完成定理的证明. 令

表示满足

的点构成的集合的内部. 则由定义

是开的, 并且根据刚刚的证明是非空的. 集合

也是闭的. 因为根据连续性, 若

并且

, 则

. 此外根据上面的证明

在

的某个邻域内为零, 因此

. 现在, 若用

表示

在

中的补, 那么

和

都是开的, 并且不相交. 此外

由于

是连通的, 因此

或

至少有一个是空集. 由于

非空, 所以

为空集, 从而

, 这就完成了定理的证明.

推论. 假设

和

是区域

内的全纯函数并且对

的某个开子集内的所有

(或者更一般地, 对一列极限点位于

的不同点序列中的

)都有

. 则

在整个

内成立.