B样条曲线曲面在MFC中的实现与应用-CSDN博客

本文链接：https://blog.csdn.net/weixin_42168902/article/details/147689735

简介：本文介绍B样条曲线曲面在计算机图形学和CAD系统中的应用，并通过MFC实现其绘制，演示如何在Windows环境下使用C++处理复杂图形。涵盖B样条曲线的定义、性质、类型，以及非均匀B样条（NURBS）曲线的特点。文章还讨论了B样条曲面的二维表示以及如何利用MFC进行图形界面设计和用户交互。掌握这些知识对于计算机辅助设计、游戏开发和模拟仿真等领域具有重要意义。 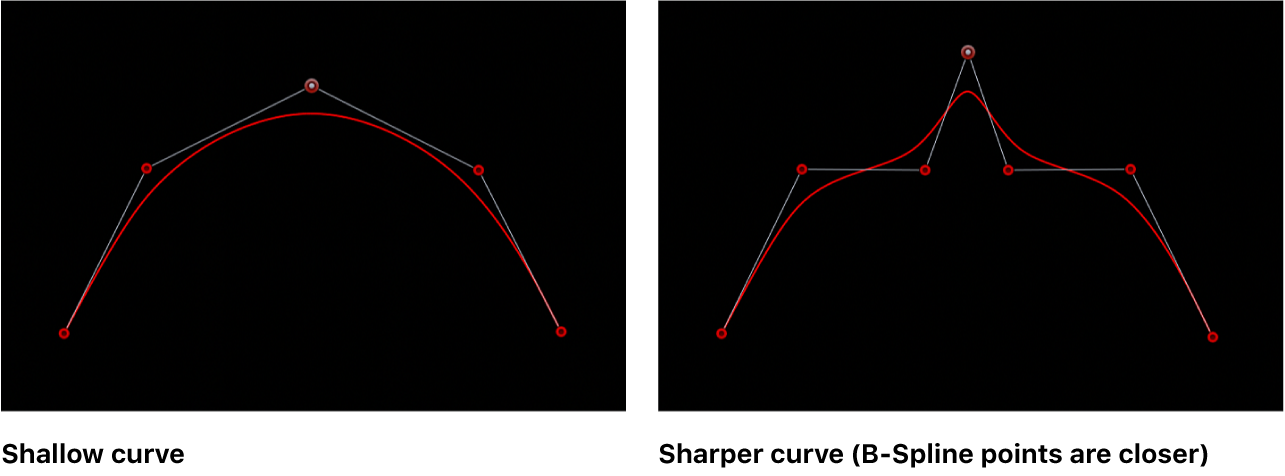B样条曲线曲面 Mfc

1. B样条曲线基础与性质

B样条曲线是计算机图形学和几何建模中广泛应用的一种参数曲线。它通过一组控制点来定义曲线形状，具有良好的局部控制特性，即修改一个控制点只会影响曲线的一部分。B样条曲线的优点在于能够表示复杂形状并且易于控制，它的一般形式由节点向量、控制点集合以及阶数（或称为度数）三个要素决定。在理解B样条曲线时，首先要熟悉其定义式，这是掌握B样条曲线性质及其应用的基础。

B样条曲线定义式可以表示为：

S(u) = \sum_{i=0}^{n} N_{i,k}(u) \cdot P_i

其中， S(u) 为曲线函数， u 是参数， N_{i,k}(u) 是k阶B样条基函数， P_i 表示第i个控制点。

B样条曲线的性质如下：

局部控制性：控制点的移动只影响曲线的一部分，提高了编辑灵活性。
多项式段连续性：B样条曲线在每个控制点处具有高阶连续性，通常在数学上表现为C^(k-1)连续。
仿射不变性：曲线的形状不会因为坐标变换而改变。

这些性质使B样条曲线在工程设计、动画制作和CAD软件中有着广泛的应用。通过对控制点和节点向量的操作，设计者可以精确地塑造所需的曲线形状。下一章，我们将详细探讨不同类型B样条曲线的特点和构造方法。

2. B样条曲线类型详解

2.1 均匀B样条曲线

2.1.1 定义与数学表示

均匀B样条曲线是一种特殊类型的B样条曲线，其控制点均匀分布，且相应的节点向量是均匀的。它在计算机辅助设计（CAD）和计算机图形学中广泛用于曲线和曲面的表示和建模。数学上，一个p阶（p为正整数）均匀B样条曲线可表示为以下形式：

[ C(u) = \sum_{i=0}^{n} N_{i,p}(u) P_i ]

其中，( N_{i,p}(u) ) 是基础函数，( P_i ) 是控制点，( u ) 是参数，( n ) 是控制点的数量减去p（阶数）。

2.1.2 均匀B样条曲线的构造方法

构造均匀B样条曲线需要定义一组控制点和确定适当的节点向量。下面是构造均匀B样条曲线的基本步骤：

确定控制点( P_i )。
设定阶数( p )。
构造均匀的节点向量( U )。
计算基础函数( N_{i,p}(u) )。
应用de Boor递归公式计算曲线上的点。

以下是通过伪代码示例来说明均匀B样条曲线的构造过程：

function ConstructUniformBasisFunctions(U, p):
    for i from 0 to length(U) - p - 1:
        N[i] = 1
    for k from 1 to p:
        alpha = (u - U[i]) / (U[i + p] - U[i])
        for i from 0 to length(U) - p - 1:
            if U[i + k] != U[i]:
                N[i] = alpha * N[i] + (1 - alpha) * N[i + 1]
    return N

function ComputeBSpinePoint(U, P, p, u):
    n = length(P) - p
    C = [0, ..., 0] // 初始化结果向量
    N = ConstructUniformBasisFunctions(U, p) // 计算基础函数
    for i from 0 to n:
        C += N[i] * P[i]
    return C

2.2 准均匀B样条曲线

2.2.1 特点及与均匀B样条的区别

准均匀B样条曲线是均匀B样条曲线的一个推广，其节点向量不完全均匀，但是控制点之间距离大体相同。这种曲线的特点是能够控制曲线的局部性质，同时维持大部分均匀B样条的特性。准均匀B样条曲线与均匀B样条的主要区别在于节点向量的构造方式。

2.2.2 准均匀B样条曲线的实现技巧

准均匀B样条曲线的实现涉及优化节点向量的选择，以便在曲线的局部区域提供更多的控制点影响，从而实现更精细的控制。以下是实现准均匀B样条曲线的一些技巧：

选取适当的节点向量，使得曲线的端点处有更高的控制点密度。
使用递归或迭代方法计算准均匀B样条曲线上的点。
通过调整控制点和节点向量，实现曲线的局部修改。

2.3 分段Bezier曲线

2.3.1 Bezier曲线与B样条曲线的关系

Bezier曲线和B样条曲线都属于参数曲线，但在数学表达和控制上有所不同。Bezier曲线是由一组控制点通过Bernstein多项式定义的曲线。B样条曲线则是一种分段的参数曲线，它将曲线分成多个段，每段由一组控制点控制。它们的关系主要体现在：

B样条曲线提供了一种更灵活的控制方式，允许对每个分段使用不同数量的控制点。
Bezier曲线可以看作是B样条曲线的一种特殊情况，即当B样条曲线的每个分段使用相同数量的控制点且节点向量是均匀的时，它就变成了Bezier曲线。

2.3.2 分段Bezier曲线的应用实例

在实际应用中，分段Bezier曲线被广泛用于字体设计、动画制作等领域。例如，Adobe Illustrator软件中就使用了分段Bezier曲线来创建和编辑矢量图形。下面是分段Bezier曲线的一个简单应用实例：

假设要设计一个字母“S”的轮廓，可以使用以下步骤：

设计一系列控制点，定义字母“S”的基本形状。
使用分段Bezier曲线，每个字母部分对应一个或多个Bezier曲线段。
通过调整控制点来优化字母的形状和曲线的光滑度。
将所有Bezier曲线段拼接在一起形成完整的字母形状。

使用这种方法，设计师可以精确地控制字母“S”的每个局部形状，实现美观的字体设计。此外，分段Bezier曲线还能够提高渲染效率，因为它仅在需要表示曲线的局部细节时才增加控制点的数量。

3. 非均匀B样条（NURBS）曲线深入分析

NURBS（Non-Uniform Rational B-Splines）曲线是计算机图形学中用于表示曲线和曲面的一种重要工具。它们是B样条曲线的推广，可以在一个更加灵活的数学框架内精确地表示二次曲线和曲面。本章将深入探讨NURBS曲线的数学基础和高级特性。

3.1 NURBS曲线的数学基础

3.1.1 权因子的作用与影响

在NURBS曲线的定义中，每个控制点都有一个与之关联的权重（权因子），它们在曲线的形状上起着决定性作用。权因子可以控制相应控制点对曲线的影响力，权重越大，控制点的影响力越强；权重越小，控制点的影响力越弱。

考虑一条定义在节点向量U上的NURBS曲线。对于曲线上的每一个点P(u)，可以用以下的有理基函数表示：

B_i,k(u) = (N_i,k(u) * w_i) / Σ(w_j * N_j,k(u))

其中，N_i,k(u)是B样条基函数，w_i是控制点P_i的权重，i是控制点的索引，k是曲线的阶数，u是曲线参数。当权重w_i为1时，NURBS曲线退化为均匀B样条曲线。

3.1.2 NURBS曲线的控制点和节点向量

NURBS曲线的形状是由控制点和节点向量共同决定的。控制点P_i定义了曲线的基本形态，节点向量U定义了曲线段的分布和参数化方式。节点向量是一个非递减序列，其长度等于曲线段数加控制点数加曲线阶数。

以一个具有n+1个控制点的k阶NURBS曲线为例，节点向量U将是一个长度为n+k+1的序列。通过改变节点向量中的节点值，可以实现曲线的局部修改，比如调整曲线的张紧度和形状，或在曲线中添加或删除节点以控制曲线的细节。

3.2 NURBS曲线的高级特性

3.2.1 几何连续性与形状控制

NURBS曲线的几何连续性是指两条曲线在连接点处的切线和曲率的一致性。NURBS提供了一种方式来保证曲线间的C^r连续性，其中r是曲线在连接点处的导数连续阶数。

通过选择合适的控制点和权重，NURBS曲线可以精确地表示圆弧、椭圆等二次曲线。这种精确性是通过调整控制点位置和权重来实现的，从而可以轻松控制曲线段的形状。

3.2.2 NURBS曲线的局部修改与编辑

NURBS曲线的一个重要特性是局部修改能力。修改一个控制点或者权重，只会影响到曲线的一部分，而不会影响整个曲线的形状。这种局部性质使得NURBS曲线非常适合于交互式设计应用，因为它允许设计者通过简单地移动控制点来微调曲线的形状，而不需要重新构造整个曲线。

局部修改通常与节点插入和删除操作相结合。通过在曲线中适当的位置插入新的节点，可以细分曲线段，从而更精细地控制曲线的局部形状。相反，删除节点可以使曲线的局部形状更为平滑。这种编辑方式，结合NURBS的几何连续性，为曲线的优化和调整提供了极大的灵活性。

graph LR
A[NURBS Curve] -->|Insert Knot| B[Curve细分]
A -->|Delete Knot| C[平滑局部形状]
B --> D[调整局部控制点]
C --> D
D -->|局部修改| E[更新曲线形状]

通过上述的分析，我们看到NURBS曲线在计算机图形学中的重要性和灵活性。随着计算机技术的不断进步，NURBS曲线在工程设计、动画制作以及3D建模中的应用越来越广泛，它已经成为了现代图形学不可分割的一部分。在下一章中，我们将探讨B样条曲面的概念及其控制技术，进一步深入理解B样条技术在曲面表示上的强大能力。

4. B样条曲面概念及控制技术

4.1 B样条曲面的定义与表示

4.1.1 控制网格的概念

B样条曲面是通过控制网格来定义的，它由一系列的控制点构成。这些控制点形成了一个三维的点阵，它们定义了曲面的大致形状，而B样条曲面是这些控制点的数学描述。控制网格的调整会影响曲面的形状，因此，控制点的位置需要精心设计和调整。在设计过程中，可以通过移动控制点来增加或减少曲面的弯曲程度。

在控制网格中，每个控制点都通过B样条曲线的基函数进行加权，通过这种方式，控制点能够对曲面产生局部影响。基函数的权重取决于控制点与曲面上点的位置关系，这为曲面提供了高度的灵活性和控制能力。

4.1.2 B样条曲面的参数化表示

B样条曲面的参数化表示是通过两个参数U和V来实现的，这两个参数形成一个参数平面。对于曲面上的每一个点，都有对应的U和V值，它们定义了该点在曲面上的位置。曲面的参数化允许它在两个方向上进行定义，这使得B样条曲面在数学上表现为一个双参数的函数，可以表示为S(u,v)，其中u和v分别在各自的区间内变化。

B样条曲面的数学定义如下： [ S(u,v) = \sum_{i=0}^{m} \sum_{j=0}^{n} N_{i,k}(u) M_{j,l}(v) P_{ij} ]

其中： - (P_{ij}) 是控制点的坐标。 - (N_{i,k}(u)) 和 (M_{j,l}(v)) 是沿着u和v方向的B样条基函数，它们依赖于节点向量和控制点的数量。 - (m) 和 (n) 分别是沿U和V方向的控制点数减去1，(k) 和 (l) 是B样条曲线的阶数。

4.2 B样条曲面的构建方法

4.2.1 双向B样条曲面的构造

双向B样条曲面是通过分别沿两个参数方向（U和V）应用B样条曲线构造方法获得的。为了构建一个双向B样条曲面，我们需要一组沿U方向的控制点和一组沿V方向的控制点。这两组控制点形成了一个控制网格，通过B样条的双线性基函数进行组合，最终构造出曲面。

双向B样条曲面的构造过程包括以下步骤： 1. 设计控制网格，确定控制点的位置。 2. 定义U方向和V方向的节点向量，它们定义了每个方向上参数区间的分割。 3. 计算每个方向上的基函数。 4. 通过基函数的组合，计算曲面上任意点的位置。

4.2.2 B样条曲面的细分与控制点调整

B样条曲面的一个重要特性是细分，它允许我们通过增加控制点来细化曲面。细分的过程是一个迭代的过程，每次迭代都将控制网格变得更细。细分技术通常用于增强曲面的细节，例如在需要精细调整曲面的特定区域时。

控制点的调整是通过修改控制点的位置来改变曲面形状的过程。调整时，需要考虑曲面的局部修改特性，以确保变化是局部的且不会对其他区域产生过大的影响。通过交互式地调整控制点，可以实现对曲面形状的精确控制。

为了调整控制点，可以使用以下方法： 1. 选择需要修改的控制点。 2. 输入新的控制点位置。 3. 更新曲面以反映控制点的更改。

flowchart LR
    A[选择控制点] --> B[输入新位置]
    B --> C[更新曲面]

下面是一个使用伪代码来展示如何调整控制点的例子：

// 定义控制点结构
struct ControlPoint {
    double x, y, z;
};

// 调整控制点位置的函数
void adjustControlPoint(ControlPoint &point, double newX, double newY, double newZ) {
    point.x = newX;
    point.y = newY;
    point.z = newZ;
    // 更新曲面的逻辑
    updateSurface();
}

// 主函数
int main() {
    ControlPoint cp = {1.0, 2.0, 3.0}; // 初始控制点
    adjustControlPoint(cp, 1.5, 2.5, 3.5); // 调整控制点位置
    return 0;
}

上述代码展示了如何定义一个控制点并调整其位置。在实际应用中，调整控制点位置后，需要调用特定的函数来更新曲面的显示，以反映这些变化。通过重复上述过程，我们可以精细控制曲面的形状，以满足特定的设计要求。

5. MFC图形绘制技术

5.1 MFC绘图基础

5.1.1 设备上下文与绘图设备

在MFC（Microsoft Foundation Classes）中进行图形绘制之前，理解设备上下文（Device Context，DC）和绘图设备的概念是至关重要的。设备上下文是一个抽象的绘图表面，它提供了访问显示设备和其他输出设备的接口。在MFC中，设备上下文通常是通过CDC类来表示的，它封装了GDI（图形设备接口）对象。

要创建一个设备上下文，你可以从CClientDC派生类中获取客户区的DC，或者使用CPaintDC在视图的OnPaint函数中绘制。使用MFC中的CDC类，可以方便地进行如绘制线条、矩形、椭圆以及显示文本等操作。

void CMyView::OnDraw(CDC* pDC)
{
    CRect rect;
    GetClientRect(&rect);  // 获取客户区大小

    // 绘制一个矩形框
    pDC->Rectangle(rect.left, rect.top, rect.right, rect.bottom);
}

在上述代码中， OnDraw 函数是处理绘图的主要函数， CDC* pDC 参数是设备上下文指针，通过它可以调用各种绘图函数，如 Rectangle 。函数 GetClientRect 用于获取客户区大小，确保绘制内容能够适应视图窗口。

5.1.2 基本图形元素的绘制方法

在MFC中，提供了多种方法用于绘制基本的图形元素，比如线条、圆形、椭圆和多边形等。这些方法通常都包含在CDC类中，下面是它们的简单用法：

线条绘制 ：CDC::MoveTo和CDC::LineTo方法用于绘制线条，必须使用MoveTo指定起始点。
矩形绘制 ：CDC::Rectangle方法可以绘制一个矩形框，也可以使用CDC::FrameRect绘制边框，CDC::FillRect填充矩形。
椭圆绘制 ：CDC::Ellipse绘制一个椭圆轮廓。
多边形绘制 ：CDC::Polygon绘制任意多边形，CDC::Polyline绘制多个连续线条。

void CMyView::OnDraw(CDC* pDC)
{
    // 移动到起点
    pDC->MoveTo(10, 10);
    // 画线到终点
    pDC->LineTo(100, 100);

    CRect rect(200, 20, 300, 120);
    pDC->Rectangle(rect); // 绘制矩形

    pDC->Ellipse(150, 30, 250, 130); // 绘制椭圆

    CPoint ptArray[] = {CPoint(350, 150), CPoint(370, 180), CPoint(390, 160)};
    pDC->Polygon(ptArray, 3); // 绘制多边形
}

5.2 MFC中B样条曲线的实现

5.2.1 利用MFC绘制B样条曲线

MFC并没有直接提供B样条曲线的绘制函数，但我们可以使用现有的GDI绘图函数或者引入第三方库来实现B样条曲线的绘制。B样条曲线的实现涉及到参数化的多项式方程，它由控制点和基函数定义。

在MFC中，我们可以通过计算B样条曲线上的点然后使用CDC的绘图函数 MoveTo 和 LineTo 将这些点连接起来绘制B样条曲线。B样条曲线的一般形式如下：

B样条曲线的参数方程通常为 B(t) = ΣNi,k(t) * Pi ，其中 t 是参数变量， Ni,k(t) 是基函数， Pi 是控制点坐标。

下面是一个简单的例子，展示了如何在MFC中绘制B样条曲线：

void DrawBSpline(CDC* pDC, const std::vector<CPoint>& controlPoints)
{
    // 计算曲线上的点并绘制
    for (double t = 0; t <= 1; t += 0.01)
    {
        // 计算当前参数t对应的曲线上的点
        CPoint pt = CalculateBSplinePoint(controlPoints, t);
        if (t == 0)
            pDC->MoveTo(pt); // 移动到起点
        else
            pDC->LineTo(pt); // 绘制到新的点
    }
}

// 你需要实现CalculateBSplinePoint函数来计算B样条曲线上的点

5.2.2 交互式编辑B样条曲线

实现B样条曲线的交互式编辑，能够让用户在图形界面中直接操作控制点，从而改变曲线的形状。在MFC中，通常会使用消息映射和控件（比如按钮、滑杆）来接收用户输入，然后实时更新曲线。

为了实现这一点，我们需要将控制点与界面元素绑定，并在用户进行操作时更新这些点的坐标，接着使用 Invalidate 或 RedrawWindow 函数来强制视图重绘。

// 假设有一个编辑控制点的消息处理函数
void CMyView::OnBnClickedEditControlPoint()
{
    // 获取用户操作的参数，比如新的控制点坐标
    CPoint newControlPoint;
    GetNewControlPoint(&newControlPoint);

    // 更新B样条曲线的控制点
    UpdateControlPoint(newControlPoint);

    // 请求重绘视图
    Invalidate();
}

// 在OnDraw函数中，使用更新后的控制点绘制B样条曲线
void CMyView::OnDraw(CDC* pDC)
{
    // 假设UpdateControlPoint已经调用，并更新了控制点
    std::vector<CPoint> controlPoints = GetUpdatedControlPoints();
    DrawBSpline(pDC, controlPoints);
}

通过以上步骤，我们能够实现一个基本的交互式B样条曲线编辑器。这不仅加深了对B样条曲线绘制的理解，而且还提高了MFC图形绘制技术的应用能力。

在后续的章节中，将介绍如何在计算机辅助设计中应用B样条曲线、在3D建模与动画制作中利用这些曲线，以及将这些技术结合起来实现一个功能完备的B样条曲线编辑器的实际案例。

6. 用户交互应用与案例分析

在本章节中，我们将深入探讨用户交互设计和应用案例。用户交互设计是确保应用程序易用性、效率和用户满意度的关键因素。通过在实际案例中应用B样条曲线和曲面技术，我们能够更好地理解这些数学工具在现代软件开发中的实际应用。本章还将介绍如何结合MFC（Microsoft Foundation Class）实现一个功能完备的B样条曲线编辑器，这是一个将理论与实践相结合的项目实例。