（六）可压缩气体的一元流动

尘盖天

于 2019-10-29 20:16:46 发布

阅读量2k

点赞数 1

分类专栏：力学

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/weixin_42237984/article/details/102802142

版权

本文介绍了可压缩气体一元流动的基本概念，包括声速的定义、特征及其与马赫数的关系。声速是气体中微小扰动波的传播速度，与等熵指数和气体常数相关。马赫数是衡量气体运动速度与声速比例的重要参数，用于区分不同类型的气流。文章还讨论了气体在变截面管中的流动规律，如密度和速度的关系，以及如何通过管道截面设计来加速气流。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

目录

可压缩气体一元流动的基本方程式

气体在变截面管中的流动

基本概念

声速：气体动力学中，声速泛指微小扰动波在流体介质中的传播速度，而不仅仅是指声音的传播速度。比如，弹拨琴弦，振动了空气，空气的压强、密度等参数发生了微弱的变化，这种状态变化在空气中形成了一种不平衡的扰动，扰动又以波的形式迅速的外传，其传播速度就是声速。

声速特征

声速的大小与扰动过程中压力的变化量同密度的变化量的比值有关，流体越容易压缩则声速就越小。
气体中的声速与等熵指数k和气体常数R有关。不同的气体有各自的声速。液体中的声速与体积弹性模量K有关，不同的液体有各自的声速。
气体的声速随着气体的状态参数的变化而变化。同一流场中，如果各点的状态参数不同，则各点的声速也不同，所以声速指的是流场中某一点在某一瞬时的声速，称为当地声速。
在同种介质中声速只是当地绝对温度的函数。不同地点不同位置气体的温度不同，声速也就不同。

对于完全气体，声速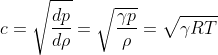： $c=\sqrt{\frac{dp}{d\rho }}=\sqrt{\frac{\gamma p}{\rho }}=\sqrt{\gamma RT}$

式中 $\gamma$ 为等熵指数， $\gamma =c_{p}/c_{v}$

马赫数

气体的运动速度和介质中声速之比，称为马赫数，用Ma表示

最低0.47元/天解锁文章

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。