优化方法求普通函数极小点MATLAB实现

问题描述

解决优化问题

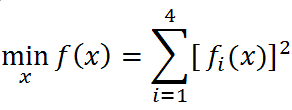
其中

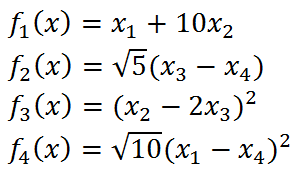
初始点为

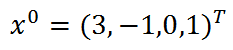
精度为1e-4

且已知问题的最优解为

函数文件

function[fun,grad,Hess]=f(x)
fun=(x(1)+10*x(2))^2+5*(x(3)-x(4))^2+(x(2)-2*x(3))^4+10*(x(1)-x(4))^4;
grad=[ 2*x(1) + 20*x(2) + 40*(x(1) - x(4))^3;
    20*x(1) + 200*x(2) + 4*(x(2) - 2*x(3))^3;
    10*x(3) - 10*x(4) - 8*(x(2) - 2*x(3))^3;
    10*x(4) - 10*x(3) - 40*(x(1) - x(4))^3];
Hess=[ 120*(x(1) - x(4))^2 + 2,                         20,                          0,     -120*(x(1) - x(4))^2;
                            20, 12*(x(2) - 2*x(3))^2 + 200,      -24*(x(2) - 2*x(3))^2,                        0;
                             0,      -24*(x(2) - 2*x(3))^2,   48*(x(2)- 2*x(3))^2 + 10,                      -10;
          -120*(x(1) - x(4))^2,                          0,                        -10, 120*(x(1) - x(4))^2 + 10 ];
end

这里直接求出一阶和二阶导

牛顿法

function [x_star]=Newton(eps)
x0=[3;-1;0;1];
k=0;  
xk=x0;                 %选择初始点
maxit=10000;           %最大迭代次数
while 1
    [~,gradk,G]=f(xk);      %设定相关参数
    res=norm(gradk);        %gradk的二范数 
    k=k+1;                  %第k次迭代
    if res<=eps||k>maxit    %算法停止条件
        break;
    end
    dk=-inv(G)*gradk;       %牛顿法确定下降方向
    
    %Armijo线搜索
    alpha_bar=1;
    rho=0.5;
    c=0.5;
    m=-1;
    while 1
        m=m+1;
        slope=gradk'*dk;
        f0=f(xk);
        x_new=xk+alpha_bar*rho^m*dk;
        f1=f(x_new);
        if f1-f0<=c*alpha_bar*rho^m*slope && m<=20
            break;
        end
    end
    alphak=alpha_bar*rho^m;       %计算步长
    
    xk=xk+alphak*dk;              %迭代核心
    fprintf('At the %d-th iteration,the residual is  %f\n',k,res);
end
x_star=xk;

这里使用Armijo线搜索来计算步长，不像前文一样特殊的二次函数精确线搜索有显式表达。
可通过更改参数来调整线搜索。

拟牛顿法

function [x_star]=DFP(eps)
x0=[3;-1;0;1];
k=0;     
xk=x0;                  %选择初始点
maxit=100000;           %最大迭代次数
Hk=eye(length(x0));     %Hk矩阵初始化
[~,gradk,~]=f(xk);      %设定相关参数
while 1
    res=norm(gradk);        %gradk的二范数 
    k=k+1;                  %第k次迭代
    if res<=eps||k>maxit    %算法停止条件
        break;
    end
    dk=-Hk*gradk;           %确定下降方向
    
    %Armijo线搜索
    alpha_bar=1;
    rho=0.5;
    c=0.5;
    m=-1;
    while 1
        m=m+1;
        slope=gradk'*dk;
        f0=f(xk);
        x_new=xk+alpha_bar*rho^m*dk;
        f1=f(x_new);
        if f1-f0<=c*alpha_bar*rho^m*slope && m<=20
            break;
        end
    end
    alphak=alpha_bar*rho^m;                     %计算步长
    
    xk=xk+alphak*dk;                            %迭代核心
    %更新Hk矩阵
    grad_temp=gradk;                            %计算yk
    [~,gradk,~]=f(xk);
    yk=gradk-grad_temp;
    deltak=alphak*dk;                           %计算deltak
    temp1=deltak*deltak'/(deltak'*yk);          %更新Hk矩阵
    temp2=(Hk*yk)*(Hk*yk)'/(yk'*(Hk*yk));
    Hk=Hk+temp1-temp2;
    fprintf('At the %d-th iteration,the residual is  %f\n',k,res);
end
x_star=xk;

拟牛顿法与牛顿法区别就是在迭代矩阵上。

共轭梯度法

function [x_star]=FR(eps)
x0=[3;-1;0;1];
k=0;   
xk=x0;                      %选择初始点
maxit=10000;                %最大迭代次数
[~,gradk,~]=f(xk);          %设定相关参数
dk=-gradk;                  %确定下降方向
while 1
    res=norm(gradk);        %gradk的二范数 
    k=k+1;                  %第k次迭代
    if res<=eps||k>maxit    %算法停止条件
        break;
    end
    
    %Armijo线搜索
    alpha_bar=1;
    rho=0.5;
    c=0.5;
    m=-1;
    while 1
        m=m+1;
        slope=gradk'*dk;
        f0=f(xk);
        x_new=xk+alpha_bar*rho^m*dk;
        f1=f(x_new);
        if f1-f0<=c*alpha_bar*rho^m*slope && m<=20
            break;
        end
    end
    alphak=alpha_bar*rho^m;        %计算步长
    
    xk=xk+alphak*dk;               %迭代核心
    %计算Beta
    grad_temp=gradk;
    [~,gradk,~]=f(xk);
    Betak=gradk'*gradk/(grad_temp'*grad_temp);
    dk=-gradk+Betak*dk; 
    fprintf('At the %d-th iteration,the residual is  %f\n',k,res);
end
x_star=xk;

总结

运行结果如下：

>> Newton(1e-4)
At the 13-th iteration,the residual is  0.000207
ans =
    0.0122
   -0.0012
    0.0020
    0.0020
    
>> DFP(1e-4)
At the 62-th iteration,the residual is  0.000157
ans =
   -0.0150
    0.0015
   -0.0045
   -0.0045 
   
>> FR(1e-4)
At the 111-th iteration,the residual is  0.000165
ans =
    0.0190
   -0.0019
    0.0076
    0.0076

为了节省篇幅只留下最后一步的结果，可以清晰对比出来算法的收敛程度。
（但是好像会受到MATLAB版本的影响，我也不太确定）
可以通过更改精度使得计算结果更加逼近精确结果，但迭代步数也肯定会相应改变。