中计算正方形面积的方法_浅谈平面图形面积计算中的技巧

浅谈平面图形面积计算中的技巧

小学平面图形面积计算一直是教学的难点，基本的图形面积计算学生尚可，但复杂的图形学生往往会感觉到困难，其实许多问题的难并不是真正的难，它的难在于我们学生没有能够阅读清楚题中信息，没有从已知信息中发现解题突破口或者没有能够整体分析数据从而导致理解不清。现结合教学中所遇到的数学问题谈谈如何找准突破口，巧妙解决平面图形面积计算的难题技巧。

突破一：利用对称，出奇制胜

如题，这是一个正方形，图中所标数的单位都是厘米，则阴影部分面积是多少?

本题解题的关键在哪?首先要阅读题目与图中数据，通过阅读先找出能够发现的有用信息——

正方形边长12厘米，面积为144平方厘米

图中阴影部分四边形并非是我们所熟悉的常规四边形，因此要求阴影部分面积必须用正方形面积-空白部分的面积。

再看空白部分——由两个完全相的直角三角形组合而成，每个三角形的面积都可以算，都是正方形面积的四分之一，用6×12÷2=36平方厘米。但问题也在于此，两个一样的三角形有重合，重合部分面积不太好找，怎么办?

这里我们需要借助一个正方形的特征来解决问题，正方形是轴对称图形，对角线也是它的一条对称轴，如图，我们将图形沿AC对折会有一条折迹，OC就是折迹的一部分——

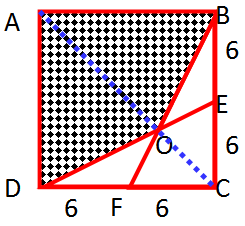
△OCE与△OCF完全重合，面积相等，同样由三角形等底等高面积相等可知△ODE=△OCF，△OBE=△OCE面积相等，那么每个小三角形都是△BCF的三分之一，所以空白部分就是4/3个△BCF=4/3×36=48平方厘米。

所以阴影部分面积=144-48=96平方厘米.

突破二：借用熟题，巧妙重组

如题：如下图有一个长12厘米，宽8厘米的长方形ABCD，已知线段DG、AH、AE、BF的长度依次分别是2、4、6、8厘米，且四边形AEPH的面积是20平方厘米，且四边形PFCG的面积是多少平方厘米?

本题许多孩子会不知如何下手，那肯定是他们阅读条件不细致所致，读题后首先不要想到的是立刻会做，而是要根据已有信息你能想到哪些信息?本题亦然，告诉我们“线段DG、AH、AE、BF的长度依次分别是2、4、6、8厘米”，结合前面条件“一个长12厘米，宽8厘米的长方形ABCD”，我们可以想到什么?对了我们应该可以知道线段CG、HD、BE、FC的长度，分别是：6、8、2、4厘米，这样你就会有这样的发现两条长边所分成的线段AH=FC=4厘米，BF=HD=8厘米，AE=CG=6厘米，BE=DG=2厘米。

但有了这样的发现，你能想到什么呢?怎样才能正确解答本题呢?我们可以对比联想回顾一道旧题——

已知长方形长10厘米，宽6厘米，中心任意一点连接与长边的中点和两宽边的三等分点得4个三角形，求阴影部分面积。相信许多同学还记得如何解答本题，我们不能单独算每个三角形的面积，而是将上下三角形组合，左右三角形组合，每组三角形分别是所在平行四边形面积的一半，从而求出阴影部分面积之和，这是老题不再叙述，但是在这里我们要借用的是老题的解题思路来解决本题——

如图，我们连接AP、CP，你就会发现已知的四边形AEPH与要求的四边形PFCG都被分成了2个三角形，并且△AHP与△CFP等底，同样△AEP与△CGP也是等底，虽然不能单独求出每个三角形的面积，但是却可以求出面积之和。

这样我们可以换一个思路迂回解答，借用旧题的思路先求出四边形AEPH与四边形PFCG的面积之和，再减去四边形AEPH的面积就得到要求的四边形PFCG的面积。

△AHP与△CFP的面积和=平行四边形AHCF的一半=4×8÷2=16平方厘米

△AEP与△CGP的面积和=平行四边形AECG一半=6×12÷2=36平方厘米

四边形AEPH与四边形PFCG的面积之和=16+36=52平方厘米

四边形PFCG的面积=52-20=32平方厘米

突破三：巧妙分拆，组合求解

如图，这个正方形的边长10厘米，图中四边形的面积是多少平方厘米?

许多孩子在处理此题的第一印象是算，算出每个三角形的面积就可以求出内部四边形的面积，问题是三角形面积怎么求?也有孩子想到了赋值的方法，但赋值不能所得答案也不相同，显然此法也不能保证，那么如何思考呢?审视题中条件，有3个数据很特别：2厘米、9厘米、3厘米。为什么放在这里?有什么用?认真观察发现9厘米对计算的作用不大，而另两个数据又应该如何处理呢?直接计算无法进行，那我们就可以换个角度用拆分比的方法来思考，分别作辅助线如下——

两条垂线一作，这样内部四边形被分成五块，四个直角三角形和一个长方形——长方形的长是3厘米，宽是2厘米。

再看4个三角形每个都和它相邻的直角三角形组成一个新的长方形——说明四边形所拆出来的每个三角形都与外部正好有一个三角形面积相等，至此我们得到这样的结果：内部四边形的面积比外部4个三角形的面积正好多一块，中心的长方形的面积——这个面积是6平方厘米。于是求内部四边形的面积转化为和差问题。

大正方形面积：10×10=100平方厘米 小长方形面积：3×2=6平方厘米

内部四边形面积：(6+100)÷2=53平方厘米

突破四：构建对称，转化求解 如题：

阴影部分1的面积比2的面积大18平方厘米，且BD=4厘米，DC=1厘米，则线段AB长多少厘米?

分析：本题许多孩子喜欢用列方程设未知数的方法求解，能够解答，但问题的思考过于复杂，本题最简洁的方法是构建对称，转化求解。那么如何构建?我们可以将FA延长1厘米到N，连接过DN BA相交于M，则ANDC是平行四边形，底边长1厘米，同样可知MADE也是平行四边形如下图——

这样通过比较可知△MBD与△AEF面积相等，△AMN与△ECD面积相等——据上可以进一步得到平行四边形ANDC与长方形ABDF之间的面积关系，面积相差36平方厘米，根据平行四边形ANDC与长方形ABDF等高不等底，可求出AB的长：36÷(4-1)=12厘米。