瓦片地图

口口子茶叶蛋

于 2024-09-13 14:51:59 发布

阅读量201

点赞数

1. 预备知识

1.1 参考椭球

地球表面是一个凸凹不平的表面，而对于地球测量而言，地表是一个无法用数学公式表达的曲面，这样的曲面不能作为测量和制图的基准面。假想一个扁率极小的椭圆，绕地球体短轴旋转所形成的规则椭球体称之为地球椭球体。

地球椭球体与地球形体非常接近，是一个形状规则的数学表面，在其上可以做严密的计算，而且所推算的元素（如长度、角度）同大地水准面上的相应元素非常接近。

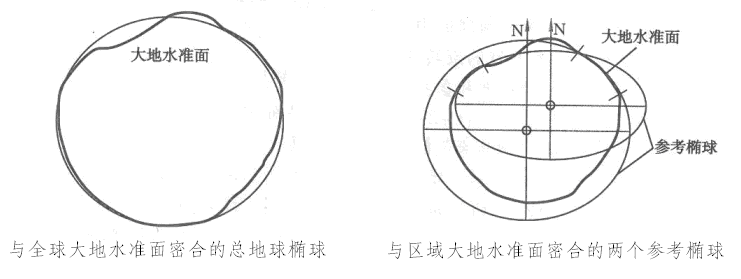
在满足地心定位和双平行条件下，确定椭球参数（长半轴、扁率）使它在全球范围内与大地体最密合的地球椭球，称为总地球椭球。

在局部区域，具有确定的椭球参数，经过局部定位和定向，同某一地区的国家大地水准面最佳拟合的地球椭球，称为参考椭球。

国际标准的参考椭球是 WGS84，Open Street Map、Google Maps 等都采用 WGS84；高德地图使用的参考椭球是 GCJ-02；百度地图使用的参考椭球是 BD-09。

1.2 地图投影

在地图学中，地图投影是一种将地球表面展平的方法，以便制作地图，这就需要一种方法将球面上的点转换为平面上的点。将球体投影到平面上，球面必然会有一定程度的变形，根据地图的目的，有些变形是可以接受的，有些则是不可以接受的，因此，为了保留球面的某些性质而牺牲其他性质，就存在不同的地图投影。

(1) 墨卡托投影

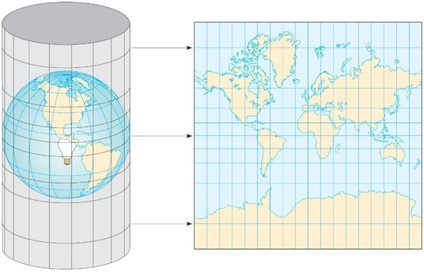
墨卡托投影法，又称麦卡托投影法、正轴等角圆柱投影，是一种等角的圆柱形地图投影法。

假想一个与地轴方向一致的圆柱切或割于地球，按等角条件，将经纬网投影到圆柱面上，将圆柱面展为平面后，即得本投影。

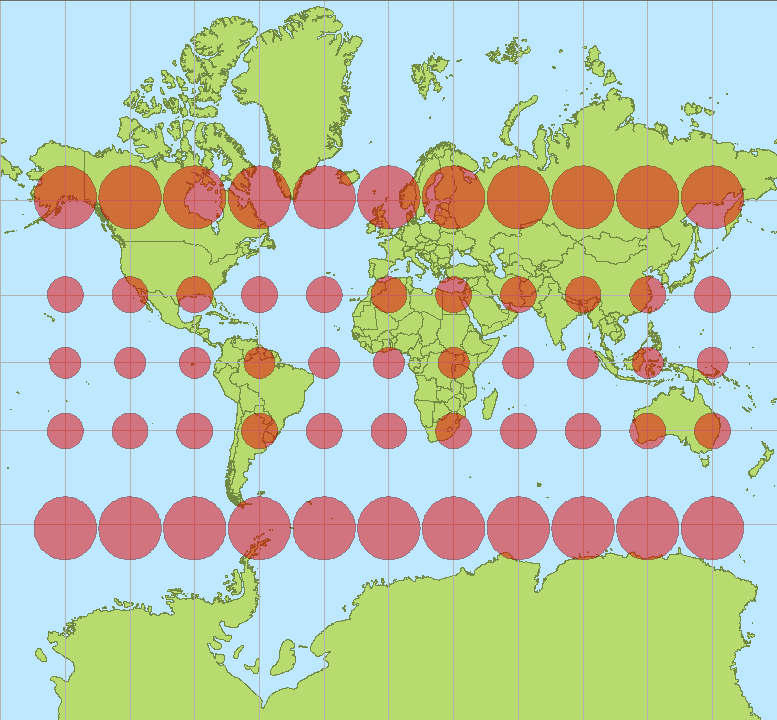
墨卡托投影可显示任两点间的正确方位，指出真实的经纬度；但会使面积产生变形，赤道地区变化最小，南北两极的变形最大。

(2) Web墨卡托投影

Web 墨卡托投影是墨卡托投影的一种变体，被 Web 地图应用业界普遍采纳。

在投影过程中，将表示地球的参考椭球体近似的作为正球体处理（正球体半径 R = 椭球体半长轴 a）。

2. 什么是瓦片地图

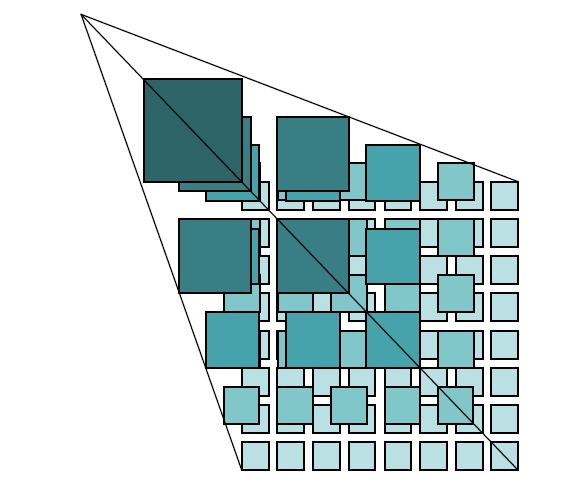
瓦片，是指将一定范围内的地图按照一定的尺寸和格式，按缩放级别或者比例尺，切成若干行和列的正方形栅格图片，切片后的正方形栅格图片被形象的称为瓦片。

瓦片地图金字塔模型是一种多分辨率层次模型，从瓦片金字塔的底层到顶层，分辨率越来越低，但表示的地理范围不变。即，每一层表示的地理范围是相同的，但自顶向下，每层划分的瓦片数越来越多，不同层间每个瓦片的分辨率相同。

瓦片的划分数量，对应不同的缩放级别（Zoom Level）。每一级别的瓦片数为：\(\displaystyle\text{\#Tiles} = 2^{level} \times 2^{level}\)

级别	瓦片数	每个瓦片表示的经度	赤道处每个像素表示的范围（m / pixel，每个瓦片宽为256像素）	比例尺	表示的区域实例
0	1	360	156 543	1:5亿	全球
1	4	180	78 272	1:2.5亿
2	16	90	39 136	1:1.5亿	次大陆地区
3	64	45	19 568	1:7千万	最大的国家
4	256	22.5	9 784	1:3.5千万
5	1 024	11.25	4 892	1:1.5千万	非洲大国
6	4 096	5.625	2 446	1:1千万	欧洲大国
7	16 384	2.813	1 223	1:4百万	小国家；美国的州
8	65 536	1.406	611.496	1:2百万
9	262 144	0.703	305.748	1:1百万	广域；大都市区
10	1 048 576	0.352	152.874	1:50万	都市区
11	4 194 304	0.176	76.437	1:25万	城市
12	16 777 216	0.088	38.219	1:15万	城镇；市区
13	67 108 864	0.044	19.109	1:7万	村庄；郊区
14	268 435 456	0.022	9.555	1:3.5万
15	1 073 741 824	0.011	4.777	1:1.5万	小型公路
16	4 294 967 296	0.005	2.389	1:8千	街道
17	17 179 869 184	0.003	1.194	1:4千	街区；公园；住址
18	68 719 476 736	0.001	0.597	1:2千	一些建筑、树
19	274 877 906 944	0.0005	0.299	1:1千	当地高速公路和交叉路口详细信息
20	1 099 511 627 776	0.00025	0.149	1:5千	一座中型建筑

3. 瓦片坐标

对于经过Web 墨卡托投影为平面的世界地图，在不同的缩放级别下，将其划分为像素为256 x 256 的瓦片。为了将瓦片加载到正确的位置拼接成完整的地图，需要对每个瓦片进行编号。不同的地图服务商采用的编号方式有所不同：

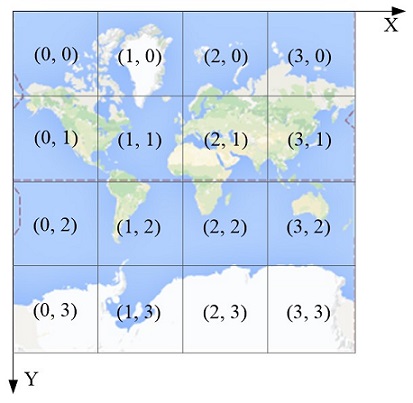
谷歌XYZ：Z 表示缩放层级；X、Y 的原点在左上角，X 从左向右，Y 从上向下。Google Maps、OpenStreetMap、Azure Maps、高德地图都采用这种编号方式。
QuadTree：微软 Bing 地图使用的编码规范，Z 表示缩放层级，同一层级的瓦片不用 X、Y 两个维度表示，而只用一个整数表示，该整数服从四叉树编码规则。微软 Bing 地图即将停用，Azure Maps 使用谷歌 XYZ 的方式进行编号。
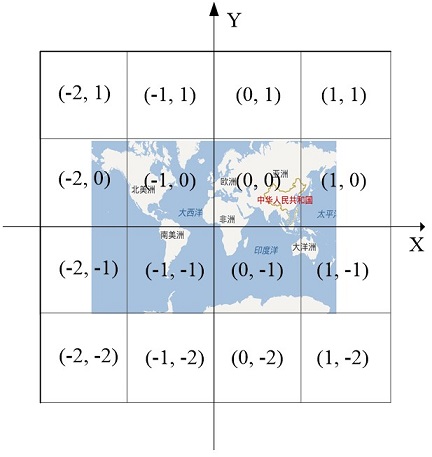
百度XYZ：百度地图使用的编码规范。Z 从 1 开始，在最高级就把地图分为四块瓦片；X、Y 的原点在经度为 0 纬度为 0 的位置，X 从左向右，Y 从下向上。

需要注意的是，虽然各地图服务商经纬度坐标系（参考椭球）不同，但某一互联网地图的经纬度坐标与瓦片坐标相互转换只与该地图商的墨卡托投影和瓦片编号的定义有关，跟地图商采用的参考椭球无关。

3.1 谷歌XYZ转换

使用谷歌XYZ时，墨卡托投影截取纬度（约85.05ºS, 约85.05ºN）之间部分的地球，使得投影后的平面地图水平方向和垂直方向长度相等。

瓦片坐标系的原点位于左上角（东经 180°，北纬约 85.05°），X 从左向右，Y 从上向下。设缩放级别为 Z，则地图被均匀切分为 \(2^Z \times 2^Z\) 个瓦片，每个瓦片像素为 \(256 \times 256\)。

经纬度坐标 \((\text{lon}, \text{lat})\) 转瓦片坐标 \((\text{tileX}， \text{tileY})\)：
- \(\displaystyle\text{tileX} = \lfloor \frac{\text{lon} + 180}{360} \times 2^Z \rfloor\)
- \(\displaystyle\text{tileY} = \lfloor (\frac{1}{2} - \frac{\ln(\tan{(\frac{\text{lat}\times \pi}{180})} + sec{(\frac{\text{lat}\times \pi}{180})})}{2\pi}) \times 2^Z \rfloor\)
经纬度坐标 \((\text{lon}, \text{lat})\) 转像素坐标 \((\text{pixelX}， \text{pixelY})\)：
- \(\displaystyle\text{pixelX} = \lfloor \frac{\text{lon} + 180}{360} \times 2^Z \times 256\ \% \ 256 \rfloor\)
- \(\displaystyle\text{pixelY} = \lfloor (\frac{1}{2} - \frac{\ln(\tan{(\frac{\text{lat}\times \pi}{180})} + sec{(\frac{\text{lat}\times \pi}{180})})}{2\pi}) \times 2^Z \times 256\ \% \ 256 \rfloor\)
瓦片坐标 \((\text{tileX}, \text{tileY})\) 转经纬度坐标 \((\text{lon}, \text{lat})\)：
- \(\displaystyle\text{lon} = \frac{\text{tileX}}{2^Z} \cdot 360 - 180\)
- \(\displaystyle\text{lat} = \arctan{(\sinh{(\pi - \frac{\text{tileY}}{2^Z} \cdot 2\pi)})} \cdot \frac{180}{\pi}\)
瓦片 \((\text{tileX}， \text{tileY})\) 内部的像素坐标 \((\text{pixelX}, \text{pixelY})\) 转经纬度坐标 \((\text{lon}, \text{lat})\)：
- \(\displaystyle\text{lon} = \frac{\text{tileX} + \frac{\text{pixelX}}{256}}{2^Z} \cdot 360 - 180\)
- \(\displaystyle\text{lat} = \arctan{(\sinh{(\pi - \frac{\text{tileY} + \frac{\text{pixelY}}{256}}{2^Z} \cdot 2\pi)})} \cdot \frac{180}{\pi}\)

另附经纬度坐标 \((\text{lon}, \text{lat})\) 转瓦片坐标 \((\text{tileX}， \text{tileY})\) 推导过程：

经纬度坐标 \((\text{lon}, \text{lat})\) 转瓦片坐标 \((\text{tileX}， \text{tileY})\) 推导过程：

将经纬度坐标 \((\text{lon}, \text{lat})\) 转换为Web墨卡托投影地图中的坐标（\(x'\)以角度为单位，\(y'\)以弧度为单位）：

\(x' = \text{lon}\)
\(\displaystyle y' = \ln(\tan{(\frac{\text{lat}\times \pi}{180})} + sec{(\frac{\text{lat}\times \pi}{180})})\)

将Web墨卡托投影地图中的坐标原点变换到左上角，并改变 Y 轴方向（\(x'\)以角度为单位，\(y'\)以弧度为单位）：

\(x'' = x' + 180\)
\(y'' = -(y' - \pi) = \pi - y'\)

转为瓦片坐标

\(\displaystyle x = \lfloor \frac{x''}{360} \times 2^Z \rfloor = \lfloor \frac{\text{lon} + 180}{360} \times 2^Z \rfloor\)
\(\displaystyle y = \lfloor \frac{y''}{2\pi} \times 2^Z \rfloor = \lfloor (\frac{1}{2} - \frac{\ln(\tan{(\frac{\text{lat}\times \pi}{180})} + sec{(\frac{\text{lat}\times \pi}{180})})}{2\pi}) \times 2^Z \rfloor\)

3.2 百度XYZ转换

百度 XYZ 坐标原点在经度为 0、纬度为 0 的位置，X 从左向右，Y 从下向上。显然，百度XYZ坐标原点与 Web 墨卡托投影地图中的坐标原点相同，X 轴方向和 Y 轴方向也与 Web 墨卡托投影地图的一致。

百度地图定义了另一种二维坐标系，称为百度平面坐标系。百度平面坐标系的坐标原点与百度 XYZ 坐标原点相同，以缩放等级 18 级为基准，规定 18 级时百度平面坐标的一个单位等于屏幕上的一个像素。平面坐标与地图所展示的级别没有关系，也就是说在 1 级和 18 级下，同一个经纬度坐标的百度平面坐标都是一致的。

百度经纬度坐标与百度平面坐标可以直接相互转换，并且与瓦片地图等级无关。经纬度坐标与瓦片坐标、像素坐标的相互转换需要以平面坐标为中间量进行转换。

百度地图的坐标转换公式如下：

经纬度坐标 \((\text{lon}, \text{lat})\) 转平面坐标 \((\text{pointX}， \text{pointY})\)：调用百度地图 API
平面坐标 \((\text{pointX}， \text{pointY})\) 转经纬度坐标 \((\text{lon}, \text{lat})\)：调用百度地图 API
平面坐标 \((\text{pointX}， \text{pointY})\) 转瓦片坐标 \((\text{tileX}， \text{tileY})\)：
- \(\displaystyle\text{tileX} = \lfloor \frac{\text{pointX} \times 2^{Z-18} }{256}\rfloor\)
- \(\displaystyle\text{tileY} = \lfloor \frac{\text{pointY} \times 2^{Z-18} }{256}\rfloor\)
平面坐标 \((\text{pointX}， \text{pointY})\) 转像素坐标 \((\text{pixelX}， \text{pixelY})\)：
- \(\displaystyle\text{pixelX} = \lfloor \text{pointX} \times 2^{Z-18} - \lfloor \frac{\text{pointX} \times 2^{Z-18}}{256}\rfloor \times 256\rfloor\)
- \(\displaystyle\text{pixelY} = \lfloor \text{pointY} \times 2^{Z-18} - \lfloor \frac{\text{pointY} \times 2^{Z-18}}{256}\rfloor \times 256\rfloor\)
瓦片 \((\text{tileX}， \text{tileY})\) 内部的像素坐标 \((\text{pixelX}, \text{pixelY})\) 转平面坐标 \((\text{pointX}， \text{pointY})\)：
- \(\displaystyle\text{pointX} = \frac{\text{tileX} \times 256 + \text{pixelX}}{2^{Z-18}}\)
- \(\displaystyle\text{pointY} = \frac{\text{tileY} \times 256 + \text{pixelY}}{2^{Z-18}}\)