壁面函数matlab,OpenFOAM 中的壁面函数（一）

本系列来看看 OpenFOAM 中的壁面函数。壁面函数的本质，是边界条件。这里主要来看看壁面函数的基本原理，OpenFOAM 中实现了的壁面函数，以及选择壁面函数的一些参考依据。

1. 壁面函数的基本原理

湍流模拟中，需要对近壁区域进行处理。一般来讲，壁面处理方法包含两类，一类是使用很细的网格，使靠近壁面的第一层网格在粘性层内($y^+ 30$)，然后用经验公式来将粘性层和对数区关联起来。下图是一个典型的壁面附近的 $U^+ text{-} y^+$ 关系图。

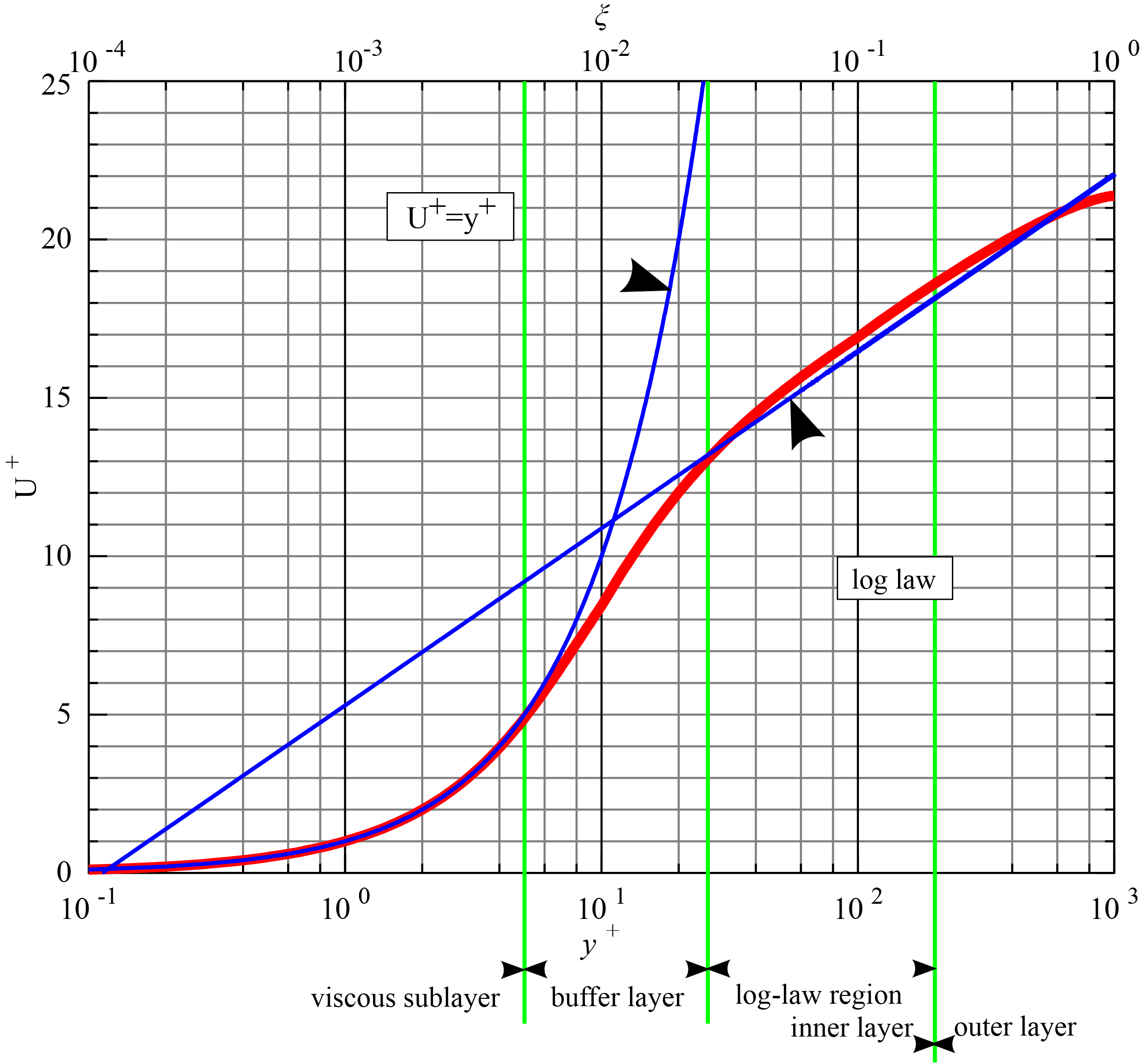
图片来自 Wikipedia:Law of the wall。

在粘性层，满足如下关系

$$

u^+ = y^+

$$

而在对数区，则满足

$$

U^+ = frac{1}{kappa}ln(Ey^+)

$$

其中 $U^+ = U/u_tau$， $y^+ = yu_tau/nu$， $u_tau = sqrt{tau_w/rho}$，$kappaapprox 0.41$，$E approx 9.8$，$y$ 表示与壁面的距离。1$)，然后里可以直接解析到粘性层的低雷诺湍流模型；另一类，不直接解析粘性层，而是将第一层网格设置在对数区($y^+>

本篇以标准壁面函数法来讨论一下壁面函数方法的基本原理，以及壁面函数在 OpenFOAM 中的实现。下面的讨论，先局限在 $k-varepsilon$ 模型，且第一层网格在对数区的情形。

先来看一下壁面函数方法需要解决什么问题。

有限体积方法中，扩散项的离散可以表示如下：

$$

nabla cdot (nu nabla U) = sum_f left [nu_f cdot (nabla U)_f right]

$$

当 $f$ 表示的是壁面边界单元时，这时就需要知道在壁面上的速度梯度 $(nabla U)_f$。壁面上一般对速度 $U$ 采用无滑移条件，如何得到正确的壁面速度梯度，这就是一个问题。这个问题有两个解决思路，一是通过实验或者 DNS 模拟等，得到一条连续的 $U-y$ 曲线，然后从这个曲线求壁面上的导数 $dU/dy$ 来得到壁面上的速度梯度；还有一种思路是，由于最终需要得到的是正确的 $nu_f cdot (nabla U)_f$ ，即壁面上的剪应力，虽然

$$

tau_w = nu cdot frac{partial U}{partial n}left. right|_w neq nu frac{U_p-U_w}{y}

$$

其中 $U_p$ 表示第一层网格中心的速度，$U_w$ 表示壁面上的速度。

但是，可以构造一个壁面上的有效粘度 $nu_{eff}$，以使下式成立

$$

tau_w = nu cdot frac{partial U}{partial n} left. right |_w = nu_{eff} frac{U_p-U_w}{y} = (nu + nu_t ) cdot frac{U_p-U_w}{y}

$$

后一种解决方法的好处是，不需要修改动量方程，直接使用 $frac{U_p-U_w}{y}$ 来代替 $frac{partial U}{partial n} left. right |_w $，然后通过设置合适的湍流粘度 $nu_t$ 的边界条件来修正壁面应力 $tau_w$。

另一方面，在对数区，$k^+$ 是常数

$$

k^+ = frac{1}{sqrt{C_mu}} \

$$

其中 $k^+ = k/u_tau^2$。

由

$$

k^+ = frac{1}{sqrt{C_mu}} = k/u_tau^2

$$

得

$$

u_tau = C_mu^{1/4}k^{1/2}

$$

于是

$$

tau_w = rho u_tau^2 = rho u_tau cdot frac{U}{U^+} = frac{rho u_tau (U_p-U_w)}{frac{1}{kappa}ln(Ey^+)}

$$

若令

$$

nu_{eff} = frac{u_tau y}{frac{1}{kappa}ln(Ey^+)}

$$

则

$$

tau_w = rho nu_{eff}cdot frac{U_p-U_w}{y}

$$

这正是上文提到的第二种解决壁面速度问题的形式。

而

$$

nu_{eff} = frac{ u_tau y}{frac{1}{kappa}ln(Ey^+)} = frac{ y^+ nu}{frac{1}{kappa}ln(Ey^+)} = nu + nu_{tw}

$$

于是得到壁面上的湍流粘度为

$$

nu_{tw} = nu cdot left(frac{kappa y^+}{ln(Ey^+)} -1 right)

$$

$y^+$ 可以通过不同的方式来得到，具体的计算方法，见后文的 nutWallFunctions 部分。

除了得到壁面上的等效湍流粘度，还需要计算靠近壁面第一层网格的湍动能生成和湍动能耗散项。

湍动能生成项计算如下：

$$

G approx tau_wcdot frac{partial (U_p -U_w)}{partial y}

$$

由速度的壁面律

$$

U^+ = frac{U_p - U_w}{u_tau} = frac{1}{kappa}ln(Ey^+) = frac{1}{kappa} ln(Efrac{yu_tau}{nu})

$$

注意，$G$ 求的是第一层网格内的值，所以，由

$$

U_p -U_w = frac{u_tau}{kappa} ln(Efrac{yu_tau}{nu})

$$

可以求得第一层网格内的梯度

$$

frac{partial (U_p -U_w)}{partial y} left. right|_p = frac{u_tau}{kappa y_p}

$$

于是

$$

G = tau_w cdot frac{u_tau}{kappa y_p}

$$

注意，这里的 $frac{U_p-U_w}{d}$，其实是速度在壁面法向方向的梯度的近似值，这一点见上文 $nu_t$ 的边界条件部分。

再来看 $varepsilon$，$varepsilon$ 的计算基于第一层网格内的湍动生成与湍动能耗散项守恒的假设，即

$$

rho varepsilon_p = G = tau_w cdot frac{u_tau}{kappa y_p} =rhocdot frac{u_tau^3}{kappa y_p}

$$

于是得

$$

varepsilon_p = frac{u_tau^3}{kappa y_p} = frac{C_mu^{3/4}k_p^{3/2}}{kappa y_p}

$$

至于 $k$，一般认为当第一层网格位于对数区时，不需要在壁面上对 $k$ 加任何限制，用零梯度边界条件即可。

2. 在 OpenFOAM 中的实现

在 OpenFOAM 中，$k$，$varepsilon$ 和 $nu_t$ 分别有对应的边界条件可以选择，壁面函数的实现是在这些边界条件里进行的。具体地说， k***WallFunction 用于指定 $k$ 的边界条件， epsilon***WallFunction 用于计算 $varepsilon$ 和 $G$ 在第一层网格内的值， nut***WallFunction 用来计算 $nu_t$ 在壁面上的值。 还有就是一个要关心的问题是这些边界条件的调用顺序，这需要通过湍流模型的一段代码来说明，以 kEpsilon 为例：

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

void kEpsilon::correct()

{

RASModel::correct();

if (!turbulence_)

{

return;

}

volScalarField G(GName(), nut_*2*magSqr(symm(fvc::grad(U_))));

epsilon_.boundaryField().updateCoeffs();

tmp epsEqn

(

fvm::ddt(epsilon_)

+ fvm::div(phi_, epsilon_)

- fvm::laplacian(DepsilonEff(), epsilon_)

==

C1_*G*epsilon_/k_

- fvm::Sp(C2_*epsilon_/k_, epsilon_)

);

epsEqn().relax();

epsEqn().boundaryManipulate(epsilon_.boundaryField());

solve(epsEqn);

bound(epsilon_, epsilonMin_);

// Turbulent kinetic energy equation

tmp kEqn

(

fvm::ddt(k_)

+ fvm::div(phi_, k_)

- fvm::laplacian(DkEff(), k_)

==

G

- fvm::Sp(epsilon_/k_, k_)

);

kEqn().relax();

solve(kEqn);

bound(k_, kMin_);

// Re-calculate viscosity

nut_ = Cmu_*sqr(k_)/epsilon_;

nut_.correctBoundaryConditions();

}

从上述代码，可以将湍流模型的具体计算过程归纳如下：

计算湍动能生成项 $G$，并修正 $G$ 在第一层网格的值。修正是通过 epsilon_.boundaryField().updateCoeffs(); 来实现的，这里调用 epsilon 的边界条件的 updateCoeffs 函数，实现的操作是修正 $G$ 和 $varepsilon$ 在第一层网格的值。

利用更新的 $G$ 构建 epsEqn，然后修改 epsEqn( epsEqn().boundaryManipulate(epsilon_.boundaryField()); )，这样做的目的是保证在下一步 solve(epsEqn)的时候，epsilonWallFunction 类型的边界所属的网格的值不会变化，而是保持在 epsilon_.boundaryField().updateCoeffs(); 这一步里设置的值(参考 cfd-online 的这个帖子)。

求解 epsEqn，得到更新的 $varepsilon$ 场。

利用更新的 $varepsilon$ 场构建并求解 kEqn，得到更新的 $k$ 场。

计算 $nu_t$，并更新 $nu_t$ 在边界上的值(nut_.correctBoundaryConditions())

至于具体的 $k$，$varepsilon$，以及 $nu_t$ 的边界条件的实现，见后文。

参考

The Finite Volume Method in Computational Fluid Dynamics An Advanced Introduction with OpenFOAM® and Matlab®

标签：tau,壁面,frac,函数,epsilon,OpenFOAM,kappa,nu

来源： https://www.cnblogs.com/petewell/p/11407881.html