OI退役笔记-018：图论（五）强连通分量（割点、割边、缩点）

最近一直在学图论，笔记的第 9 篇
记了一些基本概念，一直比较忙就没更新。笔记的
15 ~ 17 篇记录的是最短路、二分图、最小生成树之类的，有时间补充完。

强连通分量在第 9 篇已经讲了，目前求强连通分量的算法里面 Tarjan 算法值得学习。所以本篇只讲 Tarjan 算法。

一、强连通分量

求强连通分量，其一定是一个有向图。因此我们定义两种边：

假设一个图是连通的，选定一个节点为根节点，其中蓝色的边由父结点指向子节点，称为父子边；红色的边由子节点指向父节点或父节点以上的点成为返祖边。其中父子边与所有节点组成一棵树。

要求这样的图的强连通分量，我们定义两个数组：

DFN[]：记录时间戳，表示该节点是第几个搜索到的；
LOW[]：初值等于 DFN[]，但最终指向该节点只经过一条返祖边所能达到的时间戳最小的点（该返祖边可以是其子孙节点的返祖边），如下图：

不难发现，1、5、6、7 是一个强连通分量；2、3 是一个；4 自己是一个。而其中的规律在于 DFN[x] == LOW[x]。
因为，当一个节点的 LOW 等于本身的时间戳（DFN），表明其没有返祖边，或经过返祖边也不能达到自己的爹妈爷爷节点，不能与后者形成回路，因此其与之前的点不是一个强连通分量。而其与子节点是能形成强连通分量的。因此可以定义一个 stack，每次加入节点的 DFN 值，当且仅当 DFN[x] == LOW[x]时弹栈，直到 x 自己被弹栈。

代码

void tarjan(int x)
{
	LOW[x] = DFN[x] = ++sign;
	stack[++index] = x;
	// ins[x] = 1 表示 x 在栈内
	ins[x] = 1;
	
	for (int i = head[x]; i; i = e[i].nex)
	{
		int u = e[i].to;
		if (!DFN[u])
		{
			// DFN 的值是不会变的，可以用它来充当 vis[]
			tarjan(u);
			// 它所有的由父子边连接的子节点经过一条返祖边能达到的点它也能达到
			LOW[x] = min(LOW[x], LOW[u]);
		}
		else if (ins[u])
		{
			// 这个点是它的父节点，即 x 自己的返祖边
			LOW[x] = min(LOW[x], DFN[u]);
			// 有人说：后面的 DFN[u] 也可以写成 LOW[u]，
			// 针对强连通分量没有问题，但后续求割点割边问题就大了
		}
	}
	
	// 执行弹栈
	if (DFN[x] == LOW[x])
	{
		do
		{
			printf("%d ", stack[index]);
			ins[stack[index]] = 0;
			--index;
		} while (x != stack[index + 1]);
		printf("\n");
		// 每一行一个强连通分量
	}
}

以上面的图为例：
测试数据：

7 9
1 2
2 3
2 4
1 5
5 6
6 7
3 2
6 1
7 6
// 第一行 n，m：n 个点，m 条边
// 下面 m 行，每行一个 x，y，表示从 x 到 y 有一条边

输出结果：

4
3 2
7 6 5 1

PERFECT！

二、割点和割边

要看着部分一定先看懂上面！！！
割点和割边是相对无向图的
所谓割点（割顶），就是删了这个点会影响图的连通性的点，如：

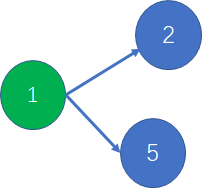
其中 1 就是割点，删了 1，2 和 5 就不连通了（忽略箭头）

如何寻找割点？
我们发现，对于边 e = vu，如果 DFN[v] > 1 且 LOW[u] >= DFN[v] 时，点 u 经过返祖边也不会到达 v 点或 v 的父节点。因此 v 是割点。而当 DFN[v] = 1 时，表明 v 是根节点，则此时只要该点出度大于等于 2，那么该点就是割点（两种情况）

代码：

void tarjan(int x)
{
    int nrc = 0;
    // num of root's child [Doge]
    DFN[x] = LOW[x] = ++sign;
    
    for (int i = head[x]; i; i = e[i].nex)
    {
        int u = e[i].to;
        if (!DFN[u])
        {
            tarjan(u);
            LOW[x] = min(LOW[x], LOW[u]);
            
            if (LOW[u] >= DFN[x] && x != root)
            	cut[x] = 1;
            if (x == root)	++nrc;
        }
        else
        	LOW[x] = min(LOW[x], DFN[u]);
    }
    
    if (x == root && nrc >= 2)
    	cut[root] = 1;
}

注意事项：若统计割点数目应该在执行完 tarjan() 后扫描 cut[]，而不应该在 tarjan() 里把 ++ans 放到 cut[k] = 1 后，这样会出错。因为有的点能同时在非根节点、是根节点两处判断处通过。
（洛谷裸题测试不到一半的分）

割边（桥）

桥，即 LOW[u] > DFN[x]。用上面的方法想想就可以。

void tarjan(int x, int pre)
{
	
	LOW[x] = DFN[x] == ++sign;
	for (int i = head[x]; i; i = e[i].nex)
	{
		if (!DFN[e[i].to])
		{
			tarjan(e[i].to, x);
			LOW[x] = min(LOW[x], LOW[e[i].to]);
			if (DFN[x] < LOW[e[i].to])
			{
				cut[i] = 1;
			}
		}
		else if (e[i].to != pre)
		{
			LOW[x] = min(LOW[x], DFN[e[i].to]);
		}
	}
}

三、缩点

缩点就是把一个有向有环图的每一个环怼成一个点，用新的点建图。
原图：

缩点后的图：

具体实现方法便是用 tarjan() 找连通分量，再建图。

void tarjan(int x)
{
	LOW[x] = DFN[x] = ++sign;
	stack[++index] = x;
	ins[x] = 1;
	
	for (int i = head[x]; i; i = e[i].nex)
	{
		int u = e[i].to;
		if (!DFN[u])
		{
			tarjan(u);
			LOW[x] = min(LOW[x], LOW[u]);
		}
		else if (ins[u])
		{
			LOW[x] = min(LOW[x], DFN[u]);
		}
	}
	
	if (DFN[x] == LOW[x])
	{
		++tot;
		do
		{
			color[stack[index]] = tot;
            sum[tot] += val[stack[index]];
            // val[] 表示点的权值
            
			ins[stack[index]] = 0;
			--index;
		} while (x != stack[index + 1]);
	}
}

MkGraph()
{
	// 枚举每一条原边，若该边两个端点不在同一个连通分量里，就建边
	for (int i = 1; i <= m; ++i)
	{ 
        if (color[e[i].from] != color[e[i].to])
            add_new(color[e[i].from], color[e[i].to]);
    }
}