Content
Intro
n linear equations, n unknowns.
E.g:
2
x
−
y
=
0
−
x
+
2
y
=
3
\begin{aligned} 2x-y = 0 \\ -x+2y = 3 \end{aligned}
2x−y=0−x+2y=3
can be written as:
[
2
−
1
−
1
2
]
[
x
y
]
=
[
0
3
]
\left[ \begin{matrix} 2 & -1 \\ -1 & 2 \end{matrix} \right] \left[ \begin{matrix} x\\ y \end{matrix} \right] = \left[ \begin{matrix} 0\\ 3 \end{matrix} \right]
[2−1−12][xy]=[03]
A
X
=
b
AX = b
AX=b
Row picture
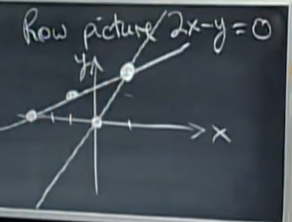
solution:
x
=
1
,
y
=
2
x = 1, y = 2
x=1,y=2
Column Picture
x
[
2
−
1
]
+
y
[
−
1
2
]
=
[
0
3
]
x\left[ \begin{matrix} 2\\-1 \end{matrix} \right] + y\left[ \begin{matrix} -1\\2 \end{matrix} \right] = \left[ \begin{matrix} 0\\3 \end{matrix} \right]
x[2−1]+y[−12]=[03]
to find a linear combination of the columns to produce the new one.
Three variables
2
x
−
y
=
0
−
x
+
2
y
−
z
=
3
−
3
y
+
4
z
=
4
\begin{aligned} 2x-y = 0 \\ -x+2y-z = 3 \\ -3y+4z = 4 \end{aligned}
2x−y=0−x+2y−z=3−3y+4z=4
A
=
[
2
−
1
0
−
1
2
−
1
0
−
3
4
]
A = \left[ \begin{matrix} 2 & -1 & 0 \\ -1 & 2 & -1\\ 0 & -3 & 4 \end{matrix} \right]
A=⎣⎡2−10−12−30−14⎦⎤
Row picture
Three planes will cross at one point
Column picture
x
[
2
−
1
0
]
+
y
[
−
1
2
3
]
+
z
[
0
−
1
4
]
=
[
0
−
1
4
]
x\left[ \begin{matrix} 2\\-1\\0 \end{matrix} \right] + y\left[ \begin{matrix} -1\\2\\3 \end{matrix} \right] + z\left[ \begin{matrix} 0\\-1\\4 \end{matrix} \right] =\left[ \begin{matrix} 0\\-1\\4 \end{matrix} \right]
x⎣⎡2−10⎦⎤+y⎣⎡−123⎦⎤+z⎣⎡0−14⎦⎤=⎣⎡0−14⎦⎤
Can I solve
A
X
=
b
AX = b
AX=b for every
b
b
b?
=
Do the linear combs of the columns fill 3-D space?
If the 3 column vectors are in the same plane, their linear combinations cannot produce b b b which is not in this plane.
Singular = not invertible
Lecture 2 Elimination
A = [ 1 2 1 3 8 1 0 4 1 ] − > [ 1 2 1 0 2 − 2 0 4 1 ] − > [ 1 2 1 0 2 − 2 0 0 5 ] A= \left[ \begin{matrix} 1&2&1 \\ 3&8&1 \\ 0&4&1 \end{matrix} \right]->\left[ \begin{matrix} 1&2&1 \\ 0&2&-2 \\ 0&4&1 \end{matrix} \right]->\left[ \begin{matrix} 1&2&1 \\ 0&2&-2 \\ 0&0&5 \end{matrix}\right] A=⎣⎡130284111⎦⎤−>⎣⎡1002241−21⎦⎤−>⎣⎡1002201−25⎦⎤
Augmented Matrix: Take b b b to the right side of A.
Row operation
[
a
b
]
[
c
d
e
f
]
=
a
[
c
d
]
+
b
[
e
f
]
\left[ \begin{matrix} a&b \end{matrix} \right] \left[ \begin{matrix} c&d\\ e&f \end{matrix} \right]= a\left[ \begin{matrix} c&d \end{matrix} \right] +b\left[ \begin{matrix} e&f \end{matrix} \right]
[ab][cedf]=a[cd]+b[ef]
The elimination process:
[
1
0
0
0
1
0
0
−
2
1
]
[
1
0
0
−
3
1
0
0
0
1
]
[
1
2
1
3
8
1
0
4
1
]
\left[ \begin{matrix} 1&0&0 \\ 0&1&0 \\ 0&-2&1 \end{matrix} \right] \left[ \begin{matrix} 1&0&0 \\ -3&1&0 \\ 0&0&1 \end{matrix} \right] \left[ \begin{matrix} 1&2&1 \\ 3&8&1 \\ 0&4&1 \end{matrix} \right]
⎣⎡10001−2001⎦⎤⎣⎡1−30010001⎦⎤⎣⎡130284111⎦⎤
Left multiplication means row operation.
Right multiplication means column operation
Lecture 3 Matrix multiplication and Inverses
Inverses
if A − 1 A^{-1} A−1 exists, A − 1 A = I A^{-1}A = I A−1A=I
Invertible = nonsingular
If I can find a non-zero vector
X
X
X with
A
X
=
0
AX = 0
AX=0
a little proof:
A X = 0 A − 1 A X = A − 1 0 = 0 X = 0 c o n t r a d i c t s w i t h n o n − z e r o AX = 0 \\ A^{-1}AX=A^{-1}0 = 0\\ X = 0 \\ contradicts\ with\ non-zero AX=0A−1AX=A−10=0X=0contradicts with non−zero
Gauss-Jordan
Assume that a row operation is
P
P
P
if
P
A
=
I
PA = I
PA=I, then
P
I
=
A
−
1
PI = A^{-1}
PI=A−1
P [ A I ] = [ I A − 1 ] P[A\ I] = [I\ A^{-1}] P[A I]=[I A−1]
Lecture 4
(
A
B
)
−
1
=
B
−
1
A
−
1
(AB)^{-1} = B^{-1}A^{-1}
(AB)−1=B−1A−1
(
A
T
)
−
1
=
(
A
−
1
)
T
(A^T)^{-1} = (A^{-1})^T
(AT)−1=(A−1)T
LU decomposition
[
1
0
−
4
1
]
[
2
1
8
7
]
=
[
2
1
0
3
]
\left[ \begin{matrix} 1 & 0 \\ -4 & 1 \end{matrix} \right] \left[ \begin{matrix} 2&1 \\ 8&7 \end{matrix} \right] = \left[ \begin{matrix} 2&1\\ 0&3 \end{matrix} \right]
[1−401][2817]=[2013]
[
2
1
8
7
]
=
[
1
0
4
1
]
[
2
1
0
3
]
\left[ \begin{matrix} 2&1 \\ 8&7 \end{matrix} \right]= \left[ \begin{matrix} 1&0 \\ 4&1 \end{matrix} \right] \left[ \begin{matrix} 2&1\\ 0&3 \end{matrix} \right]
[2817]=[1401][2013]
A
=
L
U
A = LU
A=LU
Lecture 5: Permutations
P
A
=
L
U
PA = LU
PA=LU
P
P
P: Identity matrix with reordered rows
P
−
1
=
P
T
P^{-1} = P^T
P−1=PT
R
T
R
R^TR
RTR is always symmetric:
(
R
T
R
)
T
=
R
T
R
T
T
=
R
T
R
(R^TR)^T = R^TR^{TT} = R^TR
(RTR)T=RTRTT=RTR
Vector Space
Additivity and number multiplication.
Every vector space needs the Origin.
R
n
R^n
Rn = all vectors with n real components.
We can multiply, we can add, and we stay in this vector space.
A line passing 0 is a subspace of R 2 R^2 R2























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








