为什么圆柱和圆锥的斜截口曲线是一个椭圆?
首先明确椭圆的定义
“我们把平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆(ellipse)。这两个定点叫做椭圆的焦点。两焦点间的距离叫做椭圆的焦距。”
——《高中数学选修2-1(人教版)》
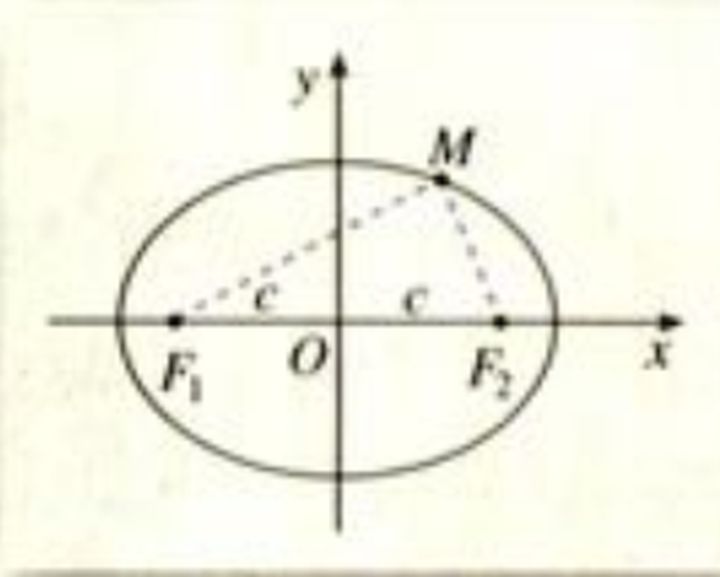
如上图,以经过椭圆两焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立直角坐标系xOy,
设M(x,y)是椭圆上任意一点,椭圆的焦距为2c(c>0),那么焦点F1、F2的坐标分别为(-c,0)、(c,0)。又设M与F1、F2的距离的和等于2a。
由椭圆的定义,椭圆就是集合
P={M||MF1|+|MF2|=2a}.
回到问题:用一个平面去截圆锥,得到的截口曲线为什么是椭圆?
历史上许多人从纯几何角度出发对这个问题进行过研究,其中数学家Germinal Dandelin的方法非常巧妙。
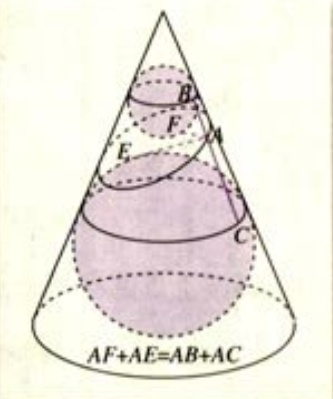
如上图,在圆锥内放两个大小不同的球,使得它们分别与圆锥的侧面、截面相切。两个球分别与截面相切于点E,F,在截口曲线上任取一点A,过点A作圆锥的母线,分别与两个球相切于点C、B
(注:C、E在大圆上,B、F在小圆上)。
由球和圆的几何性质,可以知道
AE=AC,AF=AB,
于是AE+AF=AB+AC=BC。
由切点B,C的产生方法可知,它们之间的距离BC是定值。这样截口曲线上任意一点A到两个定点E,F的距离之和为常数。
因此,由椭圆的定义可知,截口曲线就是椭圆。
可用类似的方法证明:当用一个与圆柱的母线斜交的平面去截圆柱,得到的一条截口曲线也是椭圆。
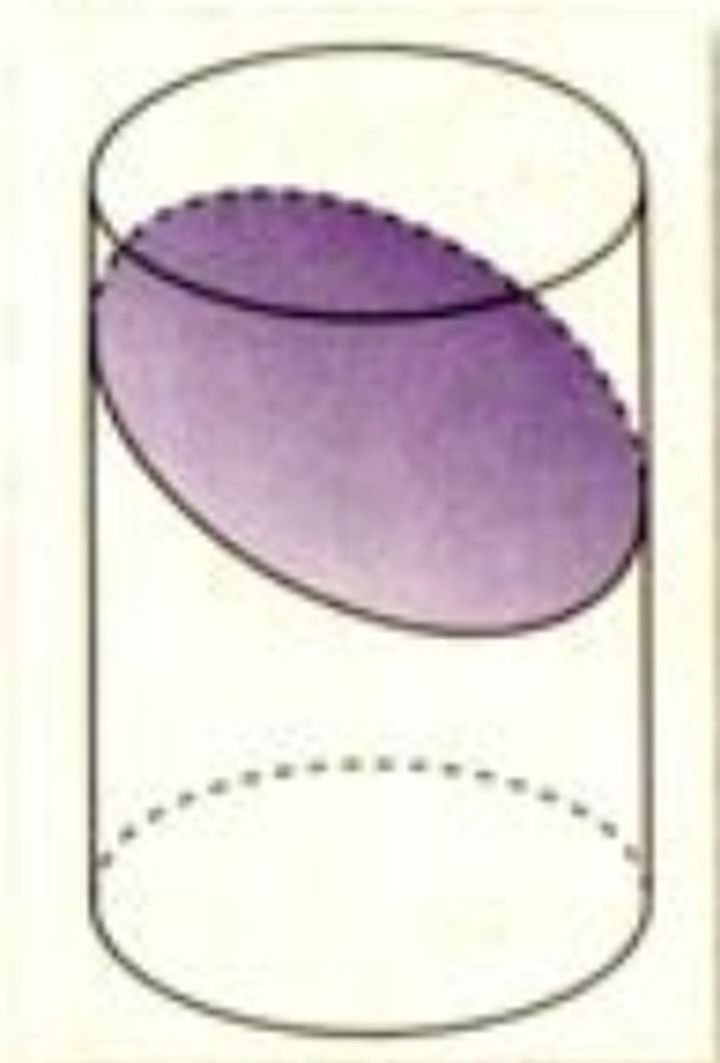







 本文介绍了圆柱和圆锥斜截面形成椭圆的几何原理,通过数学家Germinal Dandelin的方法,利用两个相切的球来解释截口曲线为何是椭圆。在截面中,点到两个固定点(球的切点)的距离之和为定值,符合椭圆的定义。这一解释揭示了椭圆在几何学中的自然出现及其与圆锥体截面的关系。
本文介绍了圆柱和圆锥斜截面形成椭圆的几何原理,通过数学家Germinal Dandelin的方法,利用两个相切的球来解释截口曲线为何是椭圆。在截面中,点到两个固定点(球的切点)的距离之和为定值,符合椭圆的定义。这一解释揭示了椭圆在几何学中的自然出现及其与圆锥体截面的关系。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








