高考冲刺倒计时，要想高考取得高分，压轴题是必须攻克的难点。在分析高考压轴题时，经常有一些“神来之笔”的答案，导致看不懂、想不到。而高考又会在这些“超难点”处反复设题，以导数压轴题中的取值技巧为例，全国一卷就连续考了四年。下面我们来分析压轴题取值是如何想到的。
更多攻克压轴题方法，小题30秒速解公式，可点击本人头条首页“专栏“查看！小题30秒，大题5分钟高分模板！高考数学极速突破140分！
经典例题：[2017年全国卷，理21]
已知函数
(Ⅰ)讨论f(x)的单调性；
(Ⅱ)若f(x)有两个零点，求a的取值范围。
解析：
(Ⅰ)f(x)的定义域为(-∞，+∞)
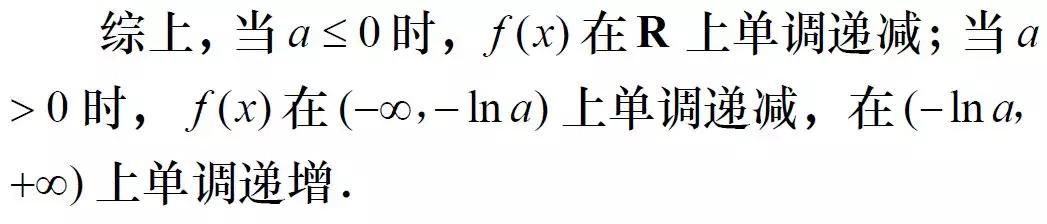
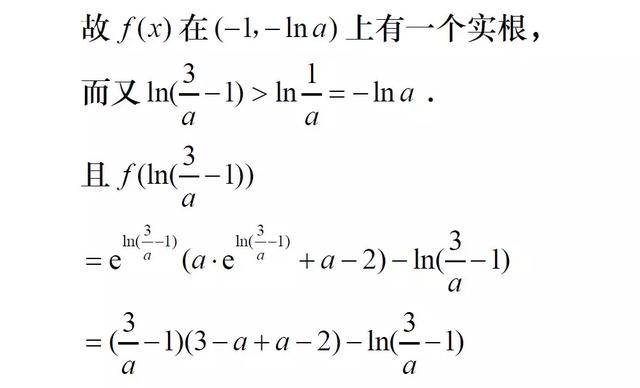
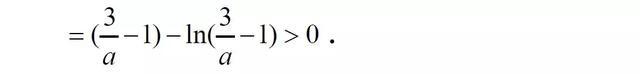
故f(x)在(-lna，ln(3/a-1))上有一个实根。又f(x)在(-∞，-lna)上单调递减，在(-lna，+∞)上单调递增，故f(x)在R上至多两个实根。
又f(x)在(-1，-lna)及(-lna，ln(3/a-1))上均至少有一个实数根，故f(x)在R上恰有两个实根。
综上，a的取值范围是(0，1)。
答案难点：
如何想到取值x=ln(3/a-1)的呢？其它的值可以吗？
思路分析：
函数f(x)的解析式是由三个基本的初
难点突破：
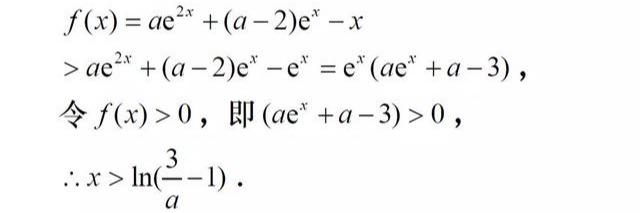
总结：从上面可以看出：”简单“取值的背后隐藏着数学思想的方法，分析答案时就要把隐藏在答案后面的思维过程挖掘出来。这样才能举一反三，融会贯通，真正做到会一题，通一类。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
