1一9数字行书写法_数独高级技巧：XYZ-wing法（20年5月26日）

所谓数独，就是将1到9的自然数填入一个9行9列的表格，根据已知的部分数字推理出所有剩余空格的数字，并满足每一行、每一列、每一个粗线宫（3*3）内的数字均含1-9，不重复。基本的表格如下图所示：

将粗线条内的9个表格称为9个宫。

题目（超5星难度）：如图，完成下面的数独表格，使每行每列和每宫中都含有1到9的9个不同自然数。

讲解思路：

数独问题的本质是逻辑推理问题，是要在满足9个数不同的条件下，不断推理出剩余的数。因此，每一步的关键是判断条件，解题的方法有很多名称，但本质都是避免出现矛盾。

对数独游戏不是很熟悉的朋友，强烈建议先基础开始看起，

18年12月7日是入门介绍（点击进入），

19年2月3日是基础方法（点击进入），

19年4月26日是排除法（点击进入）,

19年4月27日是占位法（点击进入），

19年5月6日是数对占位法（点击进入），

19年5月17日是数对占位法（点击进入），

19年10月1日是数对占位法（点击进入）,

19年11月26日是XY-wing法（点击进入）

,19年12月4日是X-wing法（点击进入）。

19年12月27日是数串法（点击进入）。

20年1月4日是数串法(点击进入)，

20年2月14日是数串法(点击进入)，

今天讲解的方法叫XYZ-wing法：如下图所示，若第1行第3列中的数只可能是a,b,c，且第1行第4列中的数只可能是a,c，且第3行第3列中的数只可能是b,c,则第1行第1列和第1行第2列不是c。

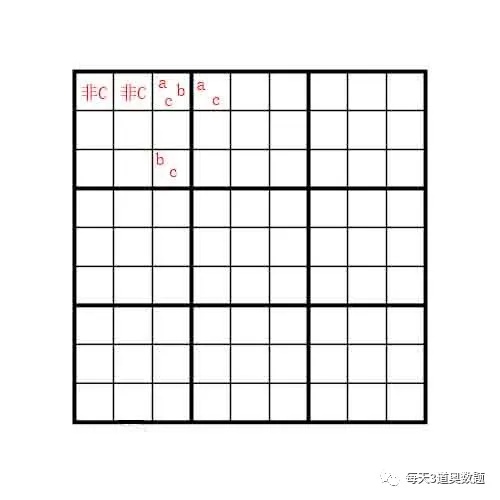
证明过程很简单，如果第1行第1列或第1行第2列是c，则第1行第4列是a，第1行第3列是b，第3行第3列没有数字可填。出现矛盾！故第1行第1列和第1行第2列不是c。这个技巧被称为XYZ-wing，属于数独高手必备技能之一，今天的题目就将用它解题。

步骤1：先思考第一个问题，标记出每个小格中的候选数字。这个问题比较简单，直接标记即可，如下图中红色小字体所示。

步骤2：再思考第二个问题，对第1行第4列的数用XY-wing法。在步骤1的图表中进行思考，第1行第1列可能是3或8，第3行第3列可能是3或5，第3行第6列可能是5或8，则根据XY-wing判别方法，第1行第4列不可能是8。用反证法可以说明这个结论，假如第1行第4列是8，则第1行第1列只能是3，第3行第3列只能是5，第3行第6列只能是8，此时第二宫中出现了2个8，出现矛盾！因此第1行第4列一定不是8。此时数独表格如下图所示。

步骤3：再思考第3个问题，用XYZ-wing法确定第1行第1列的数。在步骤2的图表中进行思考，第1行第3列可能是3、4或5，第3行第3列可能是3或5，第1行第4列可能是3或4，让a=4,b=5,c=3,符合上面XYZ-wing的关系，故第1行第1列一定不是3，因此第1行第1列只能是8。此时数独表格如下图所示。

步骤4：综上上述几个步骤，完成整个数独表格。第1行第8列只能是9，第7行第7列只能是6，第9行第5列只能是6，第6行第1列只能是1，……不断使用占位法和排除法，最终完成的数独表格如下图所示。

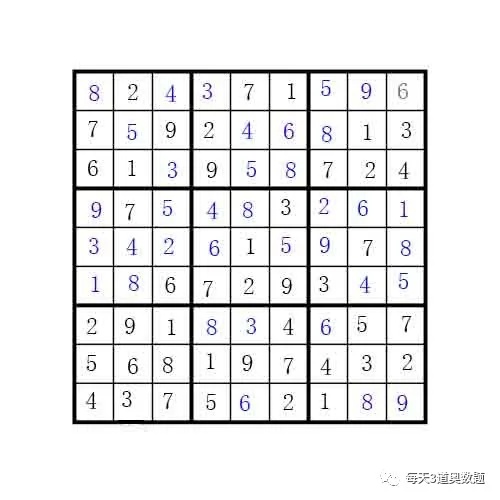
思考题（4星难度）：桌子上有2堆扑克牌，一堆是38张，另一堆是19张。小明和小红玩轮流摸牌游戏，每人每次可以从任意一堆中取走任意张牌，但只能从其中一堆中摸牌。摸走最后一张牌的人获胜。小明先摸牌，他有没有必胜策略？

我的微信公众号“每天3道奥数题”(tiantianaoshu），欢迎关注。