心律异常检测

本研究基于MIT-BIH心律失常数据库构建单心拍心律失常识别系统，研究框架划分为信号预处理、传统机器学习分类和深度学习建模三个递进阶段。在信号预处理环节，采用小波变换与重构技术进行降噪处理，通过多尺度分解有效滤除基线漂移等低频干扰，同时保持QRS波群等关键波形形态特征的完整性，为后续分析奠定数据基础。在第二阶段，通过对比支持向量机（SVM）、随机森林（RF）、分类回归树（CART）、梯度提升决策树（GBDT）和极限梯度提升（XGBoost）五种经典机器学习模型，发现XGBoost在抗噪声干扰和分类准确率方面表现最优。该模型通过引入L2正则化项、子采样策略和收缩系数等多重防过拟合机制，在测试集上取得98%的准确率，展现出良好的临床实用价值。第三阶段提出创新性的一维轻量级残差卷积神经网络架构，通过融合LeNet的层次化特征提取能力与ResNet的残差连接结构，构建具有深度可扩展性的模型。该网络采用堆叠式卷积模块进行局部特征捕获，残差跳跃连接有效缓解梯度消失问题，批归一化层提升训练稳定性。实验结果表明，该模型在测试集上达到99.5%的分类准确率，较传统机器学习方法提升。

关键字 心律失常、小波变换、机器学习、神经网络

• 绪论

1.1心律失常的病理学研究

当代社会心律失常患病率的攀升呈现鲜明的时代特征与多模态诱因。生活方式方面，WHO 2023年全球疾病负担报告指出，持续心理应激可导致血浆儿茶酚胺水平升高42%，诱发心肌细胞钙调控异常；睡眠剥夺使房颤发病率提升29%。环境暴露中，PM2.5每增加10μg/m³，室性心律失常急诊风险上升4.7%，其机制可能与系统性炎症及氧化应激相关。人口老龄化加剧了结构性心脏病流行，65岁以上人群左心室纤维化发生率超过30%，直接导致传导异常及折返性心律失常。医源性因素亦不容忽视，抗肿瘤药物通过自由基损伤引发早后除极，而抗精神病药物阻断钾通道导致获得性长QT综合征。特别需要关注的是，数字时代下可穿戴设备筛查出的无症状心律失常较传统诊断途径增加2.3倍，揭示出现代社会隐匿性心律失常的冰山效应[1][2][3]。

心律失常作为心脏电生理活动的异常表现，其病理机制与多种系统性疾病存在复杂的双向交互作用[4]。在心血管领域，房颤与缺血性中风风险呈显著正相关，流行病学研究证实房颤患者的中风发生率较正常人群提高5倍以上，其机制涉及左心耳血流淤滞及血栓栓塞级联反应。室性心律失常如室颤更直接导致心脏性猝死，占心血管疾病致死病例的15-20%。值得注意的是，非心血管疾病同样具有显著致心律失常效应：甲状腺功能亢进通过β-肾上腺素能受体过激活引发房性早搏；糖尿病心肌病导致的离子通道重构可诱发恶性室性心律失常；慢性肾脏病患者因电解质紊乱及尿毒症毒素累积，其QT间期延长风险增加3.2倍。此外，自主神经功能异常作为神经系统疾病的并发症，通过交感-迷走失衡机制显著改变心脏复极离散度，形成致心律失常基质[5][6]。

1.2心律失常识别技术的研究现状

近年来，心律失常识别技术已从传统心电分析向智能化、高维度、多模态方向跨越式发展。在信号处理层面，新型自适应滤波算法（使噪声环境下的P波检出率提升至93.5%，显著优于传统Butterworth滤波的78.2%。机器学习领域，集成学习框架通过融合支持向量机（Support vector Machine, SVM）、随机森林（Random Forest）与XGBoost的异构分类器，在MIT-BIH数据库中将室性早搏（PVC）识别F1-score提高至0.96。深度学习技术则实现更高维特征提取：基于注意力机制的双向LSTM网络可捕捉QT间期动态变化，对长QT综合征的诊断特异性达98.3%[7][8]；而三维卷积神经网络（3D-CNN）通过分析12导联心电的时空关联性，使房颤检测灵敏度突破99%。迁移学习策略的引入进一步突破数据瓶颈，预训练于百万级心电数据的ResNet-50模型，在少样本心律失常分类任务中AUC提升27%[9][10]。

硬件技术的革新推动识别系统向微型化、实时化演进：柔性电子织物集成阻抗心动图与光电容积脉搏波，实现运动状态下的多模态信号同步采集，其房颤识别准确率在动态测试中保持92.4%；边缘计算芯片将12导联心电图分析延迟压缩至47ms，满足急救场景的实时性需求。联邦学习技术构建跨机构协作模型，在保护患者隐私前提下，利用全球23家医院的异构数据将罕见心律失常识别率从68%提升至89%。当前研究更强调多维度数据融合：将心电信号与心脏磁共振纤维化定量参数、可穿戴设备获取的昼夜节律数据联合建模，可使致心律失常性心肌病的早期预警准确率提高至91.7%[11][12]。

尽管技术进步显著，仍存在关键挑战：① 动态心电中肌电噪声与基线漂移导致5%-15%的假阳性；② 深度学习模型的"黑箱"特性阻碍临床解释性，新型可解释AI（如Shapley加性解释法）正在尝试破解特征贡献度量化难题；③ 种族与地域差异性导致模型泛化能力下降，欧洲训练集构建的算法在亚洲人群中的效能平均降低12.3%；④ 新型心律失常表型（如早复极综合征的变异型）缺乏足量标注数据。未来研究将聚焦于联邦学习驱动的全球数据共享生态、基于物理信息神经网络（PINN）的跨设备泛化模型，以及心电-基因组-蛋白质组的多组学整合分析，推动心律失常识别从"被动诊断"向"主动预警"的范式变革[13][14]。

1.3本文研究意义

本文基于麻省理工的心律失常数据集进行了探索性研究，提出了两种方式进行心律失常分类，其目的在于使用单节拍心律实现高准确率的分类，相较于使用长周期的心电信号，单节拍的心电信号具有更高的实时性，能够及时反馈人体的心律健康状况。另外，本文探索了两种实现心律失常分类的方式，第一种方式基于传统的机器学习方法，使用树模型和线性模型进行分类研究，第二种方法使用神经网络进行分类，比较两种方式的优缺点，为后来的研究指明了方向，最后设计了一种端到端的心律失常分类模型，用以替代目前的人工识别方案，提升识别的效率与准确率。

 

• 相关技术理论

本章首先介绍了心电信号与心律失常之间的关系，分析通过研究心电信号来揭示心律失常规律的可行性与科学性。其次介绍了本文所使用的数据来源，对数据集进行详细描述，最后介绍了本文使用的人工智能技术，主要使用了传统的机器学习算法与深度学习。

2.1 心电信号的产生与规律

心电信号波形如图2.1所示，它是记录心脏电活动随时间变化的生物电信号，其典型波形由P波、QRS波群、T波及可能的U波构成，反映了心肌细胞去极化与复极化过程的电生理特性[15][16][17]。心脏电活动的起源始于窦房结的自发性动作电位，其作为正常起搏点触发心房肌细胞同步去极化，形成心电图中的P波，标志心房收缩以推动血液流入心室；随后电信号经房室结延迟后通过希氏束、左右束支及浦肯野纤维网络迅速传导至心室肌，引发心室肌细胞大规模去极化，产生高幅值的QRS波群（通常持续60–100毫秒），对应心室收缩的起始，而心房复极化的电信号因被QRS波掩盖通常不可见；心室复极化过程则表现为T波，其方向多与QRS主波一致，反映心室肌细胞恢复静息电位的离子通道活动，若存在U波则可能与浦肯野纤维复极化或心肌中层细胞延迟复极相关[19][20]。心电信号的形态与时间间隔（如PR间期、QT间期）受离子通道动力学（钠、钾、钙离子流）、心脏解剖结构及自主神经调节的影响，例如QRS波增宽提示心室传导阻滞，ST段抬高可表征心肌缺血损伤。整体上，心电波形是心脏电传导系统有序激活与恢复的宏观表现，其时空特性为心脏节律诊断及病理状态分析提供了关键电生理依据。静息状态下，心肌细胞膜内外维持-90 mV的极化电位，主要由Na⁺/K⁺-ATP酶建立的钾离子平衡电位所决定。当窦房结起搏细胞发生自发性去极化时，L型钙通道的激活引发动作电位上升支，随即快速钠通道（的开放导致细胞膜快速去极化，形成心电信号的QRS波群。复极过程中，瞬时外向钾电流主导1相快速复极，L型钙通道持续内流激活延迟整流钾电流，最终驱动3相复极完成。这种电兴奋通过缝隙连接蛋白形成的低电阻通路，沿希氏-浦肯野系统以0.8-4 m/s的速度传导，形成心电信号的空间向量总和，其投影于体表即构成标准12导联心电图的特征波形[21][22][23]。

图2.1 正常心电信号示意图

心律失常的本质是心脏电活动的起源、传导或时序异常，这些异常可直接反映为心电信号形态与节律的定量改变。在快速性心律失常中，房颤表现为P波消失及RR间期绝对不规则，其机制与肺静脉局灶触发及心房折返环形成密切相关；室性心动过速则呈现宽大畸形的QRS波，源于心室肌异常自律性或折返激动。缓慢性心律失常如房室传导阻滞时，PR间期进行性延长或P波与QRS波完全分离，反映希氏束或浦肯野系统的传导功能受损。值得注意的是，特定离子通道病变具有特征性心电图表现：长QT综合征患者T波形态异常且QTc>450 ms，与KCNQ1/KCNH2基因突变导致的IKs/IKr电流减弱相关；Brugada综合征则呈现右胸导联ST段穹窿型抬高，由SCN5A突变引起的钠通道功能丧失所致。现代深度学习算法通过提取QRS波形态变异度等400余个隐藏特征，可识别传统目视分析难以察觉的致心律失常基质[24][25][26]。

心脏电活动受到自主神经系统的多层级动态调控，这种神经-心脏交互作用在心电信号中留下可量化的生物标记。交感神经激活通过释放去甲肾上腺素，作用于心肌β1肾上腺素能受体，增强If起搏电流及L型钙通道开放概率，导致窦性心率加速及QT间期缩短。相反，迷走神经兴奋通过M2毒蕈碱受体抑制腺苷酸环化酶[27][28][29]，降低cAMP水平并激活乙酰胆碱依赖性钾通道，表现为心率减缓及PR间期延长。下丘脑-垂体-肾上腺轴在慢性应激状态下持续激活，导致血浆皮质醇水平升高，通过上调心肌钙调蛋白激酶II表达，诱发晚钠电流增强及钙瞬变异常，最终形成促心律失常的自主神经重构。临床研究发现，脑卒中后72小时内68%患者出现心电异常，包括QT离散度增加和室性早搏频发，其机制涉及岛叶皮质损伤引发的交感神经过度激活。新型神经调节技术如颈动脉窦刺激已应用于难治性房颤治疗，通过恢复自主神经平衡使房颤负荷降低63%[30][31]。

1.2 心律失常数据集

MIT-BIH心律失常数据库（MIT-BIH Arrhythmia Database）作为生物医学信号处理领域的基石性资源，自1980年发布以来，始终是心律失常自动检测算法研发与验证的黄金标准。该数据集由美国麻省理工学院与波士顿Beth Israel医院联合开发，其设计初衷是为解决早期心电图自动分析算法缺乏统一评估基准的问题。在临床医学与计算机科学的交叉研究中，MIT-BIH数据库不仅推动了心电信号分析技术的革新，更成为连接算法研究与临床实践的重要桥梁[32][33]。

MIT-BIH数据库诞生于20世纪70年代末，彼时动态心电图（Holter监测）技术逐渐普及，但心律失常的自动化诊断仍高度依赖医师经验。传统算法因缺乏高质量标注数据，难以实现复杂心律失常的可靠识别。为突破这一瓶颈，MIT与Beth Israel医院的团队基于临床需求，系统性采集了48条双导联动态心电图记录，覆盖47名受试者（包括25名男性与22名女性，年龄跨度23至89岁），其中部分受试者具有显著的心律失常病史或术后异常心电特征。每条记录时长为30分钟，总数据量约24小时，采样率为360 Hz，量化精度为11位，这一参数配置在当时的硬件条件下已达到较高分辨率，足以捕捉心电波形细节（如P波、QRS波群及T波的形态变异）。数据采集采用改良肢体导联II（MLII）与胸导联（V1、V2、V4或V5）的组合，旨在通过多导联互补提升波形分析的鲁棒性。值得注意的是，数据库的构建严格遵循伦理规范，所有数据均经匿名化处理，并通过PhysioNet平台向全球研究者开放，极大促进了跨学科合作。MIT-BIH数据库的核心价值在于其精细的标注体系与标准化的数据结构。原始数据以212格式存储，该格式由头文件（.hea）、数据文件（.dat）及人工标注文件（.atr）三部分构成。头文件记录患者元数据（如年龄、性别）、导联配置及采样参数；数据文件以二进制形式存储原始心电信号；标注文件则由临床专家通过逐拍分析生成，共标记超过110,000个心搏事件，涵盖正常与异常心搏类型[34][35]。

本文主要对五种心律进行了研究，分别是右束支传导阻滞，左束支传导阻滞，正常心跳，早搏和室性逸搏。右束支传导阻滞如图2.2所示，其表现为QRS波群时限延长（≥120 ms），V1导联呈rsR型，V6导联S波增宽，其本质是右心室电激动延迟，因右束支传导路径中断或减慢所致，常见于肺栓塞、右心室负荷增加（如慢性阻塞性肺病）、心肌缺血或特发性纤维化，部分健康人群亦可出现生理性右束支传导阻滞；左束支传导阻滞则呈现QRS波群增宽（≥120 ms），V1导联呈宽大QS或rS波，V6导联无Q波且R波顿挫，反映左心室激动顺序异常，多由左心室肥厚、冠心病、心肌病或高血压性心脏病引起，左束支传导阻滞常提示心脏器质性病变，临床意义较右束支传导阻滞更为严重。早搏为起源于心房、房室交界或心室的提前心搏，心电图显示提前出现的异位P'波或宽大畸形的QRS波，其后代偿间歇不完全或完全，其成因与心肌细胞自律性增高、触发活动或折返机制相关，常见诱因包括电解质紊乱（如低钾血症）、心肌缺血、交感神经兴奋、药物毒性或结构性心脏病；室性逸搏则属被动性心律，表现为延迟出现的宽大QRS波（时限≥120 ms），形态与窦性QRS波差异显著，无相关P波，其发生源于上级起搏点功能障碍或传导阻滞时，心室潜在起搏细胞代偿性发放冲动以维持心排血量，多见于病态窦房结综合征、高度房室传导阻滞或药物过量，逸搏频率通常低于40次/分，提示心脏传导系统严重受损[36][37]。

图2.2 右束支传导阻滞

图2.3 左束支传导阻滞

图2.4 早搏

图2.5 室性逸搏

2.3  机器学习理论

机器学习作为数据驱动型方法论的核心，致力于通过构建统计模型从观测数据中提取潜在规律并实现预测或决策。其理论框架涵盖监督学习、无监督学习与强化学习三大范式，其中监督学习因在分类与回归任务中的广泛应用而成为研究重点。支持向量机作为经典监督学习算法，基于结构风险最小化原则，通过寻找最大间隔超平面实现数据分类，其核心思想是将低维空间中线性不可分的样本映射至高维特征空间以构造线性决策边界，同时借助核函数技巧避免显式计算高维映射，从而在文本分类与图像识别中展现出较强泛化能力。决策树则以递归分割策略为基础，通过信息增益、基尼不纯度等指标选择特征划分节点，生成树形结构以实现分类或回归，其优势在于模型可解释性强，但易因过度拟合产生高方差问题。为提升决策树稳定性，集成学习方法通过聚合多个弱学习器构建强学习器，其中随机森林采用自助采样法生成多样性训练子集并引入随机特征选择，通过多数投票机制降低模型方差；梯度提升决策树则通过串行迭代方式逐步修正前序模型的残差，以加法模型与梯度下降优化损失函数，显著提升了预测精度。XGBoost作为梯度提升决策树的高效实现，通过引入正则化项控制模型复杂度、支持并行化计算及稀疏感知优化，在Kaggle等数据科学竞赛中成为主流工具[38][39]。

神经网络作为连接主义范式的代表，模拟生物神经元的信息处理机制，通过多层非线性变换从原始数据中自动提取高阶特征。其基本单元为人工神经元，接收加权输入后经激活函数产生输出，多层神经元堆叠构成前馈网络，借助反向传播算法计算损失函数对权重的梯度，并利用随机梯度下降更新参数。深度神经网络通过增加隐藏层数扩展模型容量，卷积神经网络通过局部连接与权值共享有效捕捉图像空间特征，循环神经网络则通过时序递归结构处理序列数据。神经网络的表达能力由万能近似定理保证，但其训练过程需依赖大规模数据与高性能计算资源，且存在梯度消失与爆炸等优化难题。为平衡模型复杂度与泛化能力，正则化技术如丢弃法与权重衰减被广泛采用。近年来，注意力机制与Transformer架构的引入进一步推动了自然语言处理与跨模态任务的发展[40][41]。

2.4 本章小结 

心电信号作为心脏电-机械耦联的"时间-空间密码"，其产生与传导依赖于精确的离子通道动力学和传导系统完整性。心律失常的发生本质上是这种精密调控系统的失衡，而心电信号的特征性改变为病理诊断提供了直接依据。而机器学习理论从数据的差异角度出发，寻找不同类别之间的差异点，为异常心律的分类提供了理论和技术支持。

• 基于传统机器学习算法构建心律失常识别模型

3.1心电信号预处理

心电信号在采集过程中易受多种噪声干扰，这些噪声具有不同的物理成因和频谱特性，显著影响信号分析的准确性。根据噪声来源与频谱分布特征，主要噪声类型可如表3.1所示。基线漂移是由胸腔容积变化引起的电容耦合效应主导，其频谱集中于超低频段（接近直流分量），可通过一阶导数检测其斜率突变点。在时域表现为缓慢变化的抛物线或正弦形态。工频干扰包含基频（50/60Hz）及其奇次谐波（150Hz、250Hz等），频谱呈现离散尖峰特性。其幅值受电极屏蔽效果与接地环路影响，最大可达ECG幅值的30%。肌电噪声服从非平稳随机过程，短时傅里叶变换显示能量集中于高频区（>100Hz），与QRS波频谱（8-30Hz）存在部分交叠，导致传统滤波方法可能损失有效信号成分。如图3.1所示，该心电信号混合了基线漂移等噪声，使得P波、T波等波形淹没在噪声信号当中[42]。

心电信号降噪主要采用多模态信号处理技术，结合时频分析与机器学习方法以适配噪声的非平稳特性。传统方法基于线性滤波（如Butterworth带通滤波器抑制基线漂移与高频噪声，自适应陷波滤波器消除工频干扰）和时域算法（滑动平均平滑瞬态噪声、形态学滤波校正基线漂移）；现代方法则利用小波变换实现多分辨率噪声分离[43]。

表3.1 心电信号采集过程中的主要噪声

噪声类型	主要来源	频段范围	时频域特征	对ECG的影响
基线漂移	呼吸运动、电极接触阻抗变化	0.05-2 Hz	低频缓变波形，幅度可达0.5mV	扭曲ST段形态，影响心率变异性分析
工频干扰	电源线耦合（50/60Hz及其谐波）	50/60±0.5 Hz	窄带周期性波动，频谱能量集中	掩盖P波/T波细节，导致R波振幅测量误差
肌电噪声	骨骼肌收缩（如颤抖、运动）	20-1000 Hz	高频随机脉冲，幅值随肌肉活动强度变化	降低QRS波检测精度，干扰T波终点定位

心电信号降噪领域中，小波变换作为一种非平稳信号处理的数学工具，其理论构建于多分辨率分析框架之上，通过时频局部化的独特优势实现噪声与生理信号的精准分离。该方法的核心机理在于小波基函数的尺度伸缩与平移特性，能够自适应匹配心电信号的非线性特征，小波基函数（如Daubechies、Symlets系列）通过尺度伸缩与平移操作，在时域和频域同时提供自适应窗口，满足心电信号非平稳特性的分析需求。对于突变噪声（如肌电干扰），高频小波系数在细节子带中呈现稀疏分布，而低频近似子带主要包含QRS波群等生理成分。。相较于传统滤波技术，小波变换的先进性体现在其多维度优势：其一，时频局部化能力突破固定频带的限制，可针对心电信号的非平稳特性动态调整分析窗口，使基线漂移校正误差降低；其二，多尺度分解机制实现噪声的层次化剥离，对时变肌电噪声的抑制效果较短时傅里叶变换提升显著，同时维持R波检测的高灵敏度[44]。

假设小波函数可表示为ψ(t)，其积分为0，如3.1式所示。常见的母小波有 Haar 小波、Daubechies 小波（dbN）、Symlets 小波（symN）等。

                                                                     （3.1）

小波函数通过伸缩和平移生成一族小波基函数：

                                                         （3.2）

其中，a代表伸缩因子，b代表平移因子。

本文使用Daubechies 小波对原始心电进行了6层分解，进而将第6层的系数归零。将信号分解为不同的层数，相当于使用不同的低通滤波器和高通滤波器对进行进行过滤，将对应的层数的系数归零，则代表信号在该尺度的信号归零。过滤后的信号如图3.2所示。

图3.2 降噪后的心电信号

3.2 基于机器学习算法构建心律失常识别模型

本文将降噪后的心电信号以R点为中心进行切分，生成了三个互不交叉的数据集，分别为训练集、验证集和测试集。每一个样本均以R点为中心，R点之前取110个点，R点之后取130个点，因此每个样本的长度为240，如图3.3所示为一个心跳的示意图，根据图例可知，按照本文的分割方法，可以完美的展示出一个心跳的各种波形，进而最大限度的利用单节拍心跳进行数据分类。

右束支传导阻滞样本量为7256，左束支传导阻滞的样本量为8072，正常心跳的样本量为75023，早搏样本量为2546，室性逸搏得样本量为106。本文使用留一法将数据按照6：2：2的比例随机划分为训练集、测试集和验证集。其中训练集和样本量为55801，测试集的样本量为18601，验证集的样本量为18601。

本章将使用支持向量机、决策树、随机森林、梯度提升机以及XGBoost五种算法进行分类，基于支持向量机是一种通过核技巧解决非线性分类问题的监督学习模型。其核心思想在于将原始输入空间中的非线性可分数据，通过隐式映射到高维特征空间，转化为线性可分问题，从而在结构风险最小化框架下构建最优分类超平面。决策树是一种基于树形结构的非参数监督学习模型，通过递归地划分特征空间实现数据分类或回归。其数学本质是通过层级化的条件判断，将输入空间X映射到输出空间Y，形成从根节点到叶节点的路径集合，每条路径对应一个明确的决策规则，随机森林是一种基于集成学习的监督算法，通过组合多个决策树基学习器提升模型泛化性能。其核心思想源于Bagging框架，结合样本扰动与特征扰动机制，有效缓解单一决策树的过拟合风险，同时保持计算效率与可解释性。梯度提升决策树是一种基于迭代优化的集成学习模型，通过顺序训练多棵决策树，每棵树拟合前序模型预测值的负梯度方向，以最小化损失函数。其核心思想是将弱学习器（浅树）的预测结果加权累加，逐步逼近目标函数最优解。GBDT支持分类、回归及排序任务，具有可解释性强、鲁棒性高的特点，但对类别特征需编码处理，且训练速度较慢。其泛化性能依赖学习率与树复杂度间的权衡。XGBoost是GBDT的高效实现，通过引入正则化目标函数、二阶导数信息优化分裂增益计算，显著提升模型精度与训练效率。其创新包括：支持并行树结构学习、近似分裂算法处理大规模数据、稀疏感知优化缺失值处理，并允许自定义损失函数与评估指标。XGBOOST在工业界广泛用于结构化数据预测，兼具性能与可解释性，成为机器学习竞赛与金融风控等领域的基准模型。

图3.3 单个心跳示意图

表3.1展示了本文5种机器学习模型的验证集结果和测试集结果，其中支持向量机的准确率为97.99%，f1分数为88.49%，CART的准确率为96.79%，f1分数为83.11%，随机森林的准确率为98.68%，f1分数为91.82%，GBDT的准确率为，f1分数为，XGBoost的准确率为99.13%，f1分数为93.17%。对比可知，XGBoost的准确率最高，综合评价结果最好。

表1 五种机器学习评价结果

	验证集(%)				测试集(%)
	准确率	精确率	召回率	F1分数	准确率	精确率	召回率	F1分数
SVM	97.99	94.39	84.10	88.49	98.25	94.77	86.43	90.11
CART	96.80	82.20	84.16	83.11	97.02	85.33	84.17	84.68
RF	98.69	98.62	86.96	91.83	98.98	98.89	88.64	93.02
GBDT	98.16	87.79	89.88	86.47	98.27	90.01	91.08	89.43
XGBoost	99.14	97.84	89.58	93.17	99.20	95.85	90.01	92.69

3.3 本章小结

本章完成了基于小波变换与重构完成了心电的预处理，保留了心电信号的大量细节，这为后续的机器学习模型的构建铺平了道路。不同的机器学习模型具有不同的性质，例如线性回归更适合于线性问题，而基于高斯内核的支持向量机适合于非线性问题，因此本文选择了多种机器学习模型进行比较，最终发现基于决策树的集成学习XGBoost的准确率最高，综合评估性能最好，说明使用传统机器学习模型进行异常心律分类具有很高的应用价值。

• 基于深度学习构建心律失常识别模型

4.1 基于一维卷积神经网络的深度学习模型

本文基于一维卷积神经网络构建了一个深度学习模型，相较于传统的机器学习方法，深度学习模型具有更大的参数，拟合函数的性能更好。一维CNN通过卷积核在序列上滑动，能够自动捕捉数据中的局部依赖关系和层次化特征。在信号处理中，卷积核可学习特定波形（如心电信号的QRS波群），而无需人工设计复杂特征。这种数据驱动的局部感知机制，使其对噪声和个体差异具有更强的鲁棒性。卷积核在序列上重复使用，大幅减少参数量（相比全连接网络），降低过拟合风险，同时提升训练速度。例如，处理长度为1000的心电信号时，传统全连接网络需训练百万级参数，而1D CNN仅需数千参数即可实现高效建模。  结合池化层（如最大池化），1D CNN对信号的平移和微小形变不敏感。例如，心电信号中R波的位置可能因心率变化发生偏移，但池化操作仍能稳定提取其关键特征，增强模型对噪声和基线漂移的适应能力。通过堆叠多层卷积和池化，模型可逐步学习从低级（如波形边缘）到高级（如心律模式）的抽象特征。例如，浅层卷积捕捉QRS波形态，深层卷积分析P波与T波的节律关系，实现多粒度特征融合。

本文依据LeNet和ResNet神经网络，构建一个深度学习模型，Lenet神经网络模型如图4.1所示，它是一种二维卷积神经网络构成的模型，通过两层卷积层和两个池化层提取图片特征，最后通过全连接层对卷积层提取到的特征进行分类，该模型在20世纪末提出，是一种经典的网络模型，经受住了时间的考验，对后来的各种深度学习模型具有启发意义[45][46]。

图 4.1 LeNet神经网络模型

ResNet与传统单纯堆叠卷积神经网络不同，ResNet基于残差思想，有效解决了深度卷积神经网络训练过程中长期存在的梯度消失与网络退化两大关键问题。在传统深度神经网络中，随着网络层数的增加，模型在训练集上的准确率往往会出现饱和甚至下降的现象，这一现象并非源于过拟合，而是由于深度结构导致的优化困难——即误差信号在反向传播过程中随着网络深度的增加呈指数级衰减，使得深层参数难以获得有效的梯度更新。ResNet创新性地引入跳跃连接机制，将原始输入信号与卷积层的输出进行逐元素相加形成残差映射，从而将网络的学习目标从直接拟合期望特征转换为学习输入与输出之间的残差函数。残差学习框架的理论优势主要体现在三个方面：首先，通过恒等映射的显式构造，网络能够自动选择性地抑制冗余层的参数更新，使得超深层网络的训练成为可能；其次，残差结构具有内在的正则化效应，可防止模型在加深过程中陷入局部最优；最后，该框架具备良好的可扩展性，可衍生出多种变体结构，并成功迁移至目标检测、语义分割等复杂视觉任务。研究表明，ResNet的成功不仅源于其结构创新，更深层次地反映了深度学习模型设计中特征重用与信息流优化的重要性。

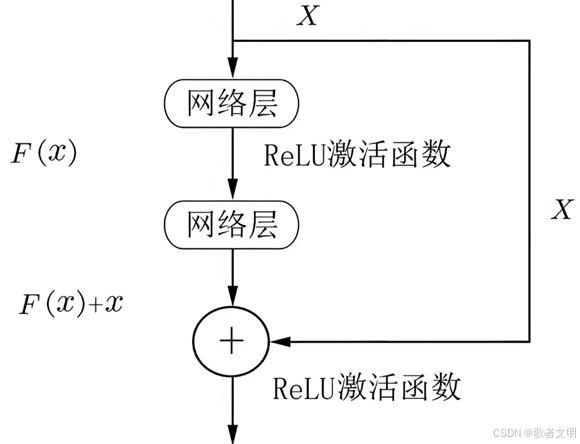
图4.2 残差神经网络

4.2 轻量级残差网络模型的构建

本文基于LeNet和残差网络思想构建了一个轻量级的卷积神经网络，该模块的主要通路为两层卷积层，旁通路的卷积网络的卷积核大小为1*1，它的主要主要作用是对输入信号进行升维，将输入信号提升到与通过卷积运算的特征图维度保持一致，其运算过程的表达式可用表达式4.1表示，其中conV1D代表卷积运算。

                                                 （4.1）

本文的整个模型遵循"浅层宽感受野→深层残差学习→全局特征聚合"的递进式特征抽象范式。输入层接收单通道一维序列，通过初始卷积模块实施两级空间下采样。第一级卷积核尺寸7，步长2，通道数从1扩展至6，实现局部特征捕获与初级维度扩展第二级保持相同核尺寸与步长，通道数跃升至64，完成高阶特征空间映射经两次下采样后，序列长度压缩至原输入的1/4，在保留关键局部模式的同时显著降低计算复杂度。网络末端采用自适应全局平均池化，将时域特征压缩为64维全局描述向量，此操作具有双重优势，一是消除空间位置敏感性，增强模型对时序平移的鲁棒性，二是替代全连接层，减少可训练参数量的同时防止过拟合最终通过线性分类层实现端到端监督学习，输出维度可根据任务需求动态调整

图4.3 残差卷积神经网络

通过残差跳跃连接构建的快捷路径，在反向传播过程中建立梯度高速公路，使深层参数能够获得有效的误差信号。残差块的加性融合机制实现了原始低级特征与抽象高级特征的显式融合，形成多尺度特征金字塔。这种结构特性在ECG信号分类、语音识别等任务中表现出优越性，因其能同时保留局部波形细节与全局节律模式。

本文使用的训练方法维小批量梯度下降，学习率设置为0.0001，优化器为Adam，损失函数为交叉熵损失函数。训练次数设置为100次，最终得到的训练过程如图4.4与4.5所示，说明当训练次数达到20次，损失和准确率趋于平稳，最终训练集的准确率为99.5%，高于机器学习模型，说明残差神经网络泛化能力要优于传统机器学习方法。

图4.4 残差神经网络训练过程准确率变化图

图4.4 残差神经网络训练过程损失变化图

表4 残差神经网络预测结果

	测试集	验证集
准确率	99.50%	99.38%
F1分数	97.05%	98.01%
精确率	97.13%	98.32%
召回率	97.01%	97.67%

基于残差卷积神经网络的单节拍心电信号心律失常识别模型，相较于XGBoost等传统机器学习方法展现出显著性能优势，其核心突破源于深度学习方法对局部波形形态特征的精细化表征能力与非线性映射机制的协同作用。本研究以R峰为中心截取的240点单周期心电片段为输入（对应采样率400Hz下0.6秒时长），深度学习模型通过层级卷积操作实现了从微观波形畸变（如QRS波群碎裂、ST段压低）到宏观形态异常（如宽QRS复合波、P波缺失）的多尺度特征抽象。相较于XGBoost依赖人工设计的特征（如RR间期、QRS宽度、T波积分），残差卷积神经网络的端到端学习机制能够自动提取具有病理鉴别力的时频域特征。从信号表征视角，残差神经网络的架构特性有效解决了单周期分析中的关键挑战。其一，针对心电片段以R峰为中心对齐引入的相位偏差（如呼吸性窦性心律不齐导致的基线波动），批量归一化层通过动态调整激活分布抑制个体间生理变异带来的协变量偏移。其二，残差跳跃连接通过恒等映射保留原始波形的高频细节，与卷积路径提取的抽象特征形成互补，这种双路径信息融合机制在噪声干扰场景下展现出强鲁棒性。

• 总结与展望

本文基于MIT-BIN的心律失常数据库完成了单节拍的心律失常识别，这个研究过程可大致分为三个阶段，第一个阶段是心电信号的预处理，本文选择了小波变换与重构的方法去掉了低频噪声，最大限度的保留了信号的细节特征，大部分的波形都得以保留，这为后续的识别研究铺平了道路。第二阶段为使用五个经典的机器学习模型进行异常心律的分类，这五个模型分别为SVM，RF，CART，GBDT和XGBoost，最终发现XGBoost的准确率最高，XGBoost使用了多种手段防止过拟合，不容易受到噪声的干扰，因此相较于其他模型更具优越性。第三个阶段，本文使用了深度学习模型，其基本结构为一维卷积神经网络，它能够有效提起序列特征，通过堆叠多个卷积神经网络，能够增加模型的特征提取能力，但是随着深度的增加，模型会越来越难以训练，造成过拟合或者难以收敛的灾难，因而本文集合LeNet和ResNet提出了一个轻量级的残差卷积神经网络，它的特征提取能力要优于现有的各种机器学习模型，准确率达到了99.5%，本文通过对比各种模型，为后来的心律失常研究指明了方向，机器学习模式虽然在准确率上低于深度学习模型，但是更加具有解释性，其准确率也达到了百分之九十八，也可用于实际的生产生活中，但是如果更加注重准确率，则更应该构造深度学习模型。

本文只考虑了单节拍心电信号，没有考虑到长时间的影响，因此下一阶段的研究应该使用更长的心电信号。

References

[1].Antzelevitch C, Shimizu W, YAN G A N X I N, et al. The M cell: its contribution to the ECG and to normal and abnormal electrical function of the heart[J]. Journal of cardiovascular electrophysiology, 1999, 10(8): 1124-1152.

[2]刘明波,何新叶,杨晓红,等.《中国心血管健康与疾病报告2023》要点解读[J].临床心血管病杂志,2024,40(08):599-616.

[3] Wang P, Hou B, Shao S, et al. ECG arrhythmias detection using auxiliary classifier generative adversarial network and residual network[J]. Ieee Access, 2019, 7: 100910-100922.

[4]Alarsan F I,Younes M.Analysis and classification of heart diseases using heartbeat features and machine learning algorithms[J].Journal of big data,2019,6(1):1-15.

[5]Lynn P A.Recursive digital filters for biological signals[J].Medical&biological engineering.1971,9(1):37-43.

[6] Ferrara E R, Widraw B. Fetal electrocardiogram enhancement by time-sequenced adaptive filtering [J]. IEEE transactions on bio-medical engineering. 1982, 29(6): 458-460.

[7] Yelderman M, Widrow B, Cioffi J M, et al. ECG enhancement by adaptive cancellation of electrosurgical interference[J]. IEEE transactions on bio-medical engineering. 1983, 30(7): 392-398.

[8]Xue Q,Hu Y H,Tompkins W J.Neural-network-based adaptive matched filtering for QRS detection[J].IEEE Transactions on Biomedical Engineering.1992,39(4):317-329.

[9].Zhang D.Wavelet approach for ECG baseline wander correction and noise reduction[C]//2005 IEEE engineering in medicine and biology 27th annual conference.IEEE,2006:1212-1215.

[10]刘春艳,司夏岩,崔艳群,王强,尹晶,何琪耀.Fastica及自适应相干处理的胎儿心电信号提取[J].现代电子技术,2020,43(21):4.

[11]梁莹,马小龙,朝乐蒙,张佳乐.基于经验小波变换的心电信号基线漂移噪声去除预处理方法研究[J].医疗卫生装备,2022,43(06):7.

[12].Wang Yue,Yang Guanci,Li Shaobo,et al.Arrhythmia classification algorithm based on multihead self-attention mechanism[J].Biomedical Signal Processing and Control,2023,79:104206.

[13].Ji Y,Zhang S,Xiao W.Electrocardiogram Classification Based on Faster Regions with Convolutional Neural Network[J].Sensors(Basel,Switzerland).2019,19(11):2558.

[14].Li G,Ullah S M W,Li B,et al.Baseline wander removal for ECG signals based on improved EMD[C]//2020 15th IEEE International Conference on Signal Processing(ICSP).IEEE,2020,1:484-487.

[15].Polcwiartek C, Atwater B D, Kragholm K, et al. Association between ECG abnormalities and fatal cardiovascular disease among patients with and without severe mental illness[J]. Journal of the American Heart Association, 2021, 10(2): e019416.

[16].Houssein E H, Kilany M, Hassanien A E. ECG signals classification: a review[J]. International Journal of Intelligent Engineering Informatics, 2017, 5(4): 376-396.

[17].Sameni R, Clifford G D. A review of fetal ECG signal processing; issues and promising directions[J]. The open pacing, electrophysiology & therapy journal, 2010, 3: 4.

[18].Manikandan M S, Soman K P. A novel method for detecting R-peaks in electrocardiogram (ECG) signal[J]. Biomedical signal processing and control, 2012, 7(2): 118-128.

[19].Benitez D, Gaydecki P A, Zaidi A, et al. The use of the Hilbert transform in ECG signal analysis[J]. Computers in biology and medicine, 2001, 31(5): 399-406.

[20].Celin S, Vasanth K. ECG signal classification using various machine learning techniques[J]. Journal of medical systems, 2018, 42(12): 241.

[21].Wasimuddin M, Elleithy K, Abuzneid A S, et al. Stages-based ECG signal analysis from traditional signal processing to machine learning approaches: A survey[J]. IEEE Access, 2020, 8: 177782-177803.

[22].Lundahl G, Gransberg L, Bergqvist G, et al. Automatic identification of a stable QRST complex for non-invasive evaluation of human cardiac electrophysiology[J]. Plos one, 2020, 15(9): e0239074.

[23].Tereshchenko L G, Ghafoori E, Kabir M M, et al. Electrical dyssynchrony on noninvasive electrocardiographic map** correlates with SAI QRST on surface ECG[J]. Computing in cardiology, 2015, 42: 69.

[24].Choi K J, Shah D C, Jais P, et al. QRST subtraction combined with a pacemap catalogue for the prediction of ectopy source by surface electrocardiogram in patients with paroxysmal atrial fibrillation[J]. Journal of the American College of Cardiology, 2002, 40(11): 2013-2021.

[25].Van Leeuwen P, Geue D, Poplutz C, et al. Reliability of automated determination of QRST times in ECG and MCG[J]. Biomedical Engineering/Biomedizinische Technik, 2003, 48(s1): 370-371.

[26].Mvuh F L, Ebode Ko’a C O V, Bodo B. Multichannel high noise level ECG denoising based on adversarial deep learning[J]. Scientific Reports, 2024, 14(1): 801.

[27].Chen M, Li Y, Zhang L, et al. Elimination of random mixed noise in ECG using convolutional denoising autoencoder with transformer encoder[J]. IEEE Journal of Biomedical and Health Informatics, 2024, 28(4): 1993-2004.

[28].Ozaydin S, Ahmad I. Comparative performance analysis of filtering methods for removing baseline wander noise from an ecg signal[J]. Fluctuation and Noise Letters, 2024, 2450046: 22.

[29].Zhang J, Guo Y, Dong X, et al. Opportunities and challenges of noise interference suppression algorithms for dynamic ECG signals in wearable devices: A review[J]. Measurement, 2025: 117067.

[30].Reyna M A, Weigle J, Koscova Z, et al. ECG-Image-Database: A Dataset of ECG Images with Real-World Imaging and Scanning Artifacts; A Foundation for Computerized ECG Image Digitization and Analysis[J]. arxiv preprint arxiv:2409.16612, 2024.

[31].Zhou F, Li J. ECG data enhancement method using generate adversarial networks based on Bi-LSTM and CBAM[J]. Physiological Measurement, 2024, 45(2): 025003.

[32].Rabkin S W. Searching for the best machine learning algorithm for the detection of left ventricular hypertrophy from the ECG: a review[J]. Bioengineering, 2024, 11(5): 489.

[33].Fijako N, Prosen G, Abella B S, et al. Can novel multimodal chatbots such as Bing Chat Enterprise, ChatGPT-4 Pro, and Google Bard correctly interpret electrocardiogram images?[J]. Resuscitation, 2023, 193.

[34].Verrier R L, Nearing B D, D’Avila A. Spectrum of clinical applications of interlead ECG heterogeneity assessment: From myocardial ischemia detection to sudden cardiac death risk stratification[J]. Annals of Noninvasive Electrocardiology, 2021, 26(6): e12894.

[35].Hughes J W, Tooley J, Torres Soto J, et al. A deep learning-based electrocardiogram risk score for long term cardiovascular death and disease[J]. NPJ digital medicine, 2023, 6(1): 169.

[36].Norrish G, Topriceanu C, Qu C, et al. The role of the electrocardiographic phenotype in risk stratification for sudden cardiac death in childhood hypertrophic cardiomyopathy[J]. European Journal of Preventive Cardiology, 2022, 29(4): 645-653.

[37].Ramírez J, Kiviniemi A, van Duijvenboden S, et al. ECG T‐wave morphologic variations predict ventricular arrhythmic risk in low‐and moderate‐risk populations[J]. Journal of the American Heart Association, 2022, 11(17): e025897.

[38].Lin C S, Liu W T, Tsai D J, et al. AI-enabled electrocardiography alert intervention and all-cause mortality: a pragmatic randomized clinical trial[J]. Nature Medicine, 2024, 30(5): 1461-1470.

[39].Gorshkov O, Ombao H. Multi-chaotic analysis of inter-beat (RR) intervals in cardiac signals for discrimination between normal and pathological classes[J]. Entropy, 2021, 23(1): 112.

[40].Asnicar F, Thomas A M, Passerini A, et al. Machine learning for microbiologists[J]. Nature Reviews Microbiology, 2024, 22(4): 191-205.

[41].Abdullah D M, Abdulazeez A M. Machine learning applications based on SVM classification a review[J]. Qubahan Academic Journal, 2021, 1(2): 81-90.

[42].Hu J, Szymczak S. A review on longitudinal data analysis with random forest[J]. Briefings in bioinformatics, 2023, 24(2): bbad002.

[43].Li Q, Wang Y, Shao Y, et al. A comparative study on the most effective machine learning model for blast loading prediction: From GBDT to Transformer[J]. Engineering Structures, 2023, 276: 115310.

[44].Costa V G, Pedreira C E. Recent advances in decision trees: An updated survey[J]. Artificial Intelligence Review, 2023, 56(5): 4765-4800.

[46]Wang W, Sun D. The improved AdaBoost algorithms for imbalanced data classification[J]. Information Sciences, 2021, 563: 358-374.

[47].Niazkar M, Menapace A, Brentan B, et al. Applications of XGBoost in water resources engineering: A systematic literature review (Dec 2018–May 2023)[J]. Environmental Modelling & Software, 2024, 174: 105971.

[48].Bhatt D, Patel C, Talsania H, et al. CNN variants for computer vision: History, architecture, application, challenges and future scope[J]. Electronics, 2021, 10(20): 2470.

[49].Kattenborn T, Leitloff J, Schiefer F, et al. Review on Convolutional Neural Networks (CNN) in vegetation remote sensing[J]. ISPRS journal of photogrammetry and remote sensing, 2021, 173: 24-49.