频率派和贝叶斯派
硬币模型
对于一个问题,从概率派和贝叶斯派看起来是完全不一样的,其最主要的区别就是对于一个问题中模型参数的认识。
假设抛一枚硬币,设硬币朝上的概率为
θ
\theta
θ
频率派认为通过重复试验的统计结果可以估计
θ
\theta
θ,估计方法为极大似然估计(MLE)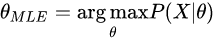
贝叶斯派认为
θ
\theta
θ服从某个分布,这个分布即为先验知识
根据贝叶斯公式:
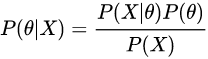
而
θ
\theta
θ与服从的某个分布与样本
X
X
X无关,因此
P
(
X
)
P(X)
P(X)可拿掉,
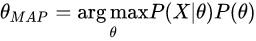
频率派和MLE(极大似然估计)
假设一个人从来没见过硬币,对于硬币的形状密度分布等一无所知,只知道概率分布是0-1分布,也就是说,不是正面就是反面。那么对于
θ
\theta
θ也就只能根据实验的事实结果来猜测,也就是最大似然估计(MLE)。
总共抛了10次硬币, 7 次为正面,此次的投掷实验
x
x
x 的似然函数为:
L
(
x
;
θ
)
=
p
(
x
∣
θ
)
=
(
10
7
)
θ
7
(
1
−
θ
)
3
L(x;\theta)=p(x\mid \theta)=\binom{10}{7}\theta^{7}(1-\theta)^{3}
L(x;θ)=p(x∣θ)=(710)θ7(1−θ)3
求解似然函数极值,即可得:
θ
M
L
E
=
0.7
\theta_{MLE}=0.7
θMLE=0.7

也就是说,下一次抛硬币出现正面的概率,可以认为是0.7
贝叶斯派和MAP(最大后验估计)
对于贝叶斯派来说,我们并不会对硬币形状一无所知,我们相信造币局造出来的硬币是质地相当均匀的,一般称之为先验信息。结合此先验信息和抛掷硬币实验结果,再次估算 θ \theta θ
还是总共抛了10次硬币,7 次为正面,但是由于我们相信硬币的制造工艺,把
θ
\theta
θ控制在某正态分布范围内,如
θ
∼
N
(
0.5
,
0.
1
2
)
\theta \sim N(0.5, 0.1^2)
θ∼N(0.5,0.12)。
此次的投掷实验
x
x
x的后验概率为:
p ( θ ; x ) = p ( x ∣ θ ) = ( 10 7 ) θ 7 ( 1 − θ ) 3 1 0.1 2 π e − 1 2 ( θ − 0.5 0.1 ) 2 p(\theta;x)=p(x\mid \theta)=\binom{10}{7}\theta^{7}(1-\theta)^{3}\frac{1}{0.1\sqrt{2\pi }}e^{-\frac{1}{2}(\frac{\theta - 0.5}{0.1})^2} p(θ;x)=p(x∣θ)=(710)θ7(1−θ)30.12π1e−21(0.1θ−0.5)2
同样求极值
P
P
P, 可以求得
θ
≈
0.558
\theta \approx 0.558
θ≈0.558

线性回归概率视角
线性回归的模型为
Y
=
W
T
X
Y=W^TX
Y=WTX, 由一些点拟合出一条直线。
更通用的模型
Y
=
F
(
W
,
X
)
Y=F(W, X)
Y=F(W,X)
下面分别使用MLE和MAP求解参数
W
W
W
最大似然估计(MLE)
使用MLE,
频率派认为参数
W
W
W为确定值,
因此考虑噪声
ε
\varepsilon
ε,
Y
=
W
T
X
+
ε
Y=W^TX+\varepsilon
Y=WTX+ε,
并假设噪声
ε
\varepsilon
ε服从高斯分布,即
ε
∼
N
(
0
,
σ
2
)
\varepsilon \sim N(0, \sigma^2)
ε∼N(0,σ2)。
由此可得到
Y
Y
Y的期望和方差,
E
[
Y
]
=
E
(
W
T
X
+
ε
)
=
E
(
W
T
X
)
+
E
(
ε
)
E[Y]=E(W^TX+\varepsilon)=E(W^TX)+E(\varepsilon)
E[Y]=E(WTX+ε)=E(WTX)+E(ε)
V
a
r
[
Y
]
=
V
a
r
(
W
T
X
+
ε
)
=
V
a
r
(
W
T
X
)
+
V
a
r
(
ε
)
Var[Y]=Var(W^TX+\varepsilon)=Var(W^TX)+Var(\varepsilon)
Var[Y]=Var(WTX+ε)=Var(WTX)+Var(ε)
由于 W W W为固定参数,给定 X X X, W T X W^TX WTX也为常数,
因此 Y ∼ N ( W T X , σ 2 ) Y \sim N(W^TX, \sigma^2) Y∼N(WTX,σ2)
似然函数表示为:
l
(
w
)
=
P
(
Y
∣
X
,
W
)
=
∏
i
=
1
n
1
2
π
σ
e
(
−
1
2
(
y
i
−
w
T
x
i
σ
)
2
)
\begin{aligned} l(w) & = P(Y|X, W) \\ &=\prod_{i=1}^{n}\frac{1}{\sqrt{2\pi}\sigma }e^{({-\frac{1}{2}(\frac{y_i-w^Tx_i}{\sigma })^2})} \end{aligned}
l(w)=P(Y∣X,W)=i=1∏n2πσ1e(−21(σyi−wTxi)2)
n n n为样本数量
两边取对数得

求解最优值

为了降低过拟合的风险,表达式添加一项
L
1
/
L
2
L1/L2
L1/L2损失
L1损失(LASSO回归)
J ( w ) = L ( w ) + λ ∣ w ∣ J(w)=L(w)+\lambda \left | w \right | J(w)=L(w)+λ∣w∣
L2损失(岭回归)
J ( w ) = L ( w ) + λ ∥ w ∥ 2 J(w)=L(w)+\lambda \left \| w \right \|^2 J(w)=L(w)+λ∥w∥2
最大验估计(MAP)
与MLE沿用同一个模型。
由贝叶斯公式可得:
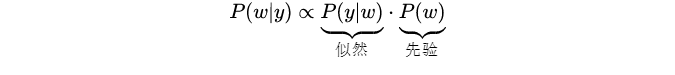
且似然为
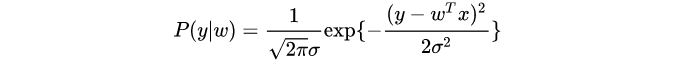
相较与频率派,
贝叶斯对参数
w
w
w有一个先验估计,
先验估计:假设
w
w
w服从高斯分布
w
∼
N
(
0
,
σ
w
2
)
w \sim N(0, \sigma_w^2)
w∼N(0,σw2)
得
p ( w ) = 1 ( 2 π ) σ w e x p ( − 1 2 ( ∥ w ∥ 2 σ w 2 ) ) \begin{aligned} p(w)=\frac{1}{(\sqrt{2\pi})\sigma_w}exp{(-\frac{1}{2}(\frac{ \left \| w\right \|^2}{\sigma_w^2} ))} \end{aligned} p(w)=(2π)σw1exp(−21(σw2∥w∥2))
取对求解参数

令:
λ
=
σ
σ
w
2
\lambda = \frac{\sigma}{\sigma_w^2}
λ=σw2σ
则损失函数为
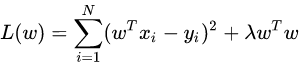
与L2正则化的最小二乘估计相同。
总结
最小二乘估计等价于极大似然估计MLE,且噪声服从高斯分布;
正则化最小二乘估计等价于极大后验概率估计MAP,且噪声服从高斯分布。
若MAP先验采用拉普拉斯分布,则推导出的与MLE采用L1正则化项的结果保持一致。
而中心极限定理告诉我们,当样本量足够大时,样本均值的分布慢慢变成正态分布,此时均值为0,也就是为什么要假设噪声服从均值为0的高斯分布。























 1925
1925











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








