摘要
本文描述了一种基于Diffle-Hellman密钥协定协议的两方私有集合交集(PSI)协议。在理想的排列+随机语言模型中,该协议被证明可以安全抵抗恶意方。
对于小集合来说(500个项目甚至更少),我们的协议需要最少的时间和通信,相比于任何已知的PSI协议,即使是那些只有半诚实安全的和不基于Diffle-Hellman的协议。这是20年间对经典的Diffle-Hellman PSI协议的少数显著改进之一。
我们的协议实际上是一个通用转换,它从一类密钥协定协议构造PSI。这一转变的灵感来自于赵、达赫曼-解决和贾雷奇(CTRSA 2016)的技术的启发,我们通过几个重要的方式进行简化和优化,以实现我们更高的效率。
1介绍
在一个私有集合交集(PSI)协议中,Alice提供了一个项目的输入集合 X X X,Bob提供了一个输入集合 Y Y Y,然后其中一方或两方学习 X ∩ Y X \cap Y X∩Y。而对于对方不在交集中的信息,则完全无法获得。许多最引人注目的安全多方计算的现实世界应用是PSI的直接应用或PSI的紧密变体,如私人联系人发现。
PSI技术的最先进水平。最近,PSI协议已经成为典型具体性能改进的重点。目前对于PSI来说已经有了几种协议范例,但在这片文章中我们重点关注的是两种最实用的方法:Diffle-Hellman协议和不经意传输(OT)扩展协议。其他的协议范例(FHE,RSA,通用MPC)则要慢很多数量级。
Diffle-Hellman协议。第一个也是可以说是最简单的PSI协议是由Huberman、Franklin和Hogg设计,但其根源可以追溯到Meadows。这是一种半诚实的协议,要求在Diffie-Hellman群的幂中与集合中项目的数量成比例。因为这个协议过于遵循Diffie-Hellman密钥协议,所以半诚实安全的变体设计空间相当有限。DH-PSI协议已经在一些工作中针对恶意安全得到了加强。迄今为止最有效的方法是由De Cristofaro、Kim和Tsudik设计。另一个有效的恶意变体是由Jarecki&Liu设计,尽管它实现了一个稍微宽松输入独立安全保证的功能。
OT扩展协议。另一类的PSI协议是基于OT扩展的。借助于OT扩展,各方可以只用少量不变数量的公钥操作生成许多不经意传输实例。通过基于许多OT的PSI,生成的PSI协议中的公钥操作(指数)的数量只与安全参数相关,而与输入集的大小无关。这一类中的PSI协议包括[11、36、42-47]。
一般来说,基于OT的协议比基于Diffie-Hellman的协议(明显)更快,但需要更多的通信。然而,Pinkas等人最近的工作提出了一种基于OT的协议,其通信(和运行时间)比基于Diffie-Hellman的PSI略少。
为什么要关注基于Diffie-Hellman的PSI协议呢?相比于基于OT的PSI协议,基于DH的PSI协议要慢得多,研究它有什么价值呢?我们有以下几个原因:
■在某些情况下,通信成本远远比计算成本更重要。作为一个具体的例子,Ion等人[30,31]报告了他们在谷歌中一个类似PSI功能的真实部署。他们选择部署Diffie-Hellman PSI,并解释他们选择的原因如下:有些令人惊讶的是,对于我们考虑的离线“批计算”场景,通信成本比计算重要得多。对于涉及多个业务的安全协议尤其如此,因为服务器不能共同定位(广域网解决方案)。网络本质上是共享的,而且在共享网络中添加CPU比扩大网络容量要便宜得多。我们改进的DH-PSI协议在基于DH和基于OT的协议中通信量是最低的。
■考虑在小集合上的PSI的范围。例如,PrivateDrop系统加强了Apple的AirDrop特性通过执行一个用户的整个地址簿(几千个项目)和另一个用户的个人标识符(例如,电话号码和电子邮件地址,可能有10项)的PSI协议,以确定是否一个用户出现在另一个用户的地址簿中。在另一个示例中,双方可能希望使用其可用日历时间的PSI来安排一次会议。基于dh的PSI协议对于这些输入大小是最便宜的(几百项的等大小集,或者更大的集合是几千个项目);我们对DH-PSI的改进提供了进一步的改进。
基于OT的PSI协议使用OT扩展,其“基本OT”每个都需要公钥操作(指数级)。具体地说,使用迄今为止最有效的1/2的OT协议[38],128个基本OT需要花费3个×128=384组通信元素和5个×128=640次求幂。这已经比我们在200大小的集上改进的DH-PSI协议更昂贵,这意味着对于这个大小的集,我们的协议必然比任何基于OT扩展的协议都便宜。事实上,基于ot的协议要超过我们的平衡点,在快速网络(10Gbps)上为500到1000个项目之间,在慢网络(50Mbps)上需要有超过1000个项目。
■对于基于OT的PSI协议,由于[43]最近对恶意PSI进行的改进,半诚实和恶意协议之间的性能差距已经相当小了。对于基于DH的PSI的情况则有很大不同:相对于半诚实PSI,最有效的恶意PSI也要慢5倍,需要2.5倍的通信。对于基于DH的PSI,我们的新方法基本上缩小了半诚实和恶意之间的性能差距。
■最后,[29]的半诚实的DH-PSI协议是一个相当经典的协议,但在20多年来并没有得到改进。我们新的半诚实协议变体是第一个对DH-PSI的通信成本进行改进的,而且改进并不小(超过40%)。甚至我们的恶意变体也比经典的半诚实协议更有效。我们所知道的唯一可比较的改进是Jarecki和Liu,他们仅改善了计算成本,根据我们的经验提高约5-15%。
1.1 相关工作
自引入以来,已经提出了几种技术来提高PSI的性能。在本节中,我们将概述现有的高效PSI协议,并更重点关注由于公钥技术而具有线性通信复杂性的解决方案。从这里开始,我们假设每个集合都有 n n n项,其中每个项都有 σ \sigma σ位长度。我们让 λ \lambda λ和 κ \kappa κ分别表示统计安全和计算安全参数。
最早的PSI协议是在20世纪80-90年代的[29,39]中提出的,并在随机语言模型中被证明可以安全地对抗半诚实的对手。这些协议仍然是基于差异-海尔曼的协议之间的比较的基础。
Freedman等人在标准模型中引入了可以安全抵抗半诚实和恶意对手的PSI协议。他们的协议是基于不经意多项式估值(OPE)的,其使用加法同态加密(AHE)来实现,如Paillier加密方案。基于OPE技术,Kissner和Song提出了不同集操作的协议,例如二次运算上的集交与集并和数据集大小的通信复杂度。DachmanSoled等人提出了一种改进的PSI协议的结构,它在恶意对手面前实现了 O ( n κ 2 l o g 2 ( n ) + κ n ) O(n \kappa^2log^2(n)+ \kappa n) O(nκ2log2(n)+κn)组元素和 O ( n 2 κ l o g ( n ) + n κ 2 l o g 2 ( n ) ) O(n^2\kappa log(n)+n\kappa^2log^2(n)) O(n2κlog(n)+nκ2log2(n))指数的通信。他们避免了一般的零知识证明,因为Shamir的秘密共享包含一个Reed-Solomon编码。随后,Hazay和Nissim扩展了基于OPE的PSI协议,并将完美隐藏承诺方案的效率与OPRF(不经意伪随机函数)评估协议结合起来。[26]中的PSI协议导致 O ( n ( 1 + log σ ) ) O(n(1+\log{\sigma} )) O(n(1+logσ))组元素的通信,以及 O ( n ( 1 + log log ( n ) + log ( σ ) ) ) O(n(1+\log{\log(n)}+\log(\sigma ))) O(n(1+loglog(n)+log(σ)))模块指数的计算。随后,我们还研究了该问题的其他变体,如隐藏大小集合交集、PSI基数、私有交集和。在这里,我们强调了具有线性复杂度的基于公钥的PSI协议。
半诚实的PSI协议。目前最先进的半诚实PSI(独立于协议是否基于DH)是[11,36,42]的协议,最好的协议取决于计算相对于通信的相对成本。我们的协议涉及到将值编码为多项式,并且这种技术以某种形式出现在几个PSI协议中。其中一个协议是由Cho,Dachman-Soled和Jarecki设计的。我们的协议主要建立在他们的协议基础上,我们稍后将进行更详细的讨论。Pinkas等人设计的另一个协议是基于OT扩展的,但也在一个多项式中对某些值进行编码。在我们工作出现之前,该协议具有最低的通信,不包括那些基于昂贵的FHE或RSA累加器的协议。
对于基于RSA的PSI方法,据我们所知,Cristofaro和Tsudik的工作及其改进提出了在半诚实的环境中通信最低的PSI协议。这个协议是基于RSA累加器的。后一种协议实现的通信仅略高于不安全的交叉协议(在该协议中,双方只发送其输入的哈希)。然而,由于RSA操作的成本,它们的计算需求(至少是 n log ( n ) n\log(n) nlog(n)RSA指数)使该协议在实践中非常昂贵。我们将在后面的第5.2节中进一步比较RSA方法。
恶意的PSI协议。Jarecki和Liu提出了第一个存在恶意对手时基于OPRF的线性复杂度PSI协议。他们为Dodis-Yampolskiy PRF f k ( x ) = g 1 / ( k + x ) f_k(x)=g^{1/(k+x)} fk(x)=g1/(k+x)构建了一个OPRF协议,该协议需要 O ( 1 ) O(1) O(1)模块指数,并具有常数轮通信。然而,它们的OPRF功能的安全计算协议是在公共参考字符串(CRS)模型中,其中CRS包括一个安全的RSA组合,它必须由可信方预先生成,或者在安全的两方计算模型中生成时意味着高开销。该协议的另一个限制是,它的安全证明在输入域上运行穷尽搜索。这意味着在安全参数中输入域应该是多项式的。
De Cristofaro等人提出了一种在恶意设置下安全的PSI协议,它在不限制输入域大小的情况下,实现了与之前的工作相同的渐近界,并且不需要CRS模型。他们的PSI协议需要在一个循环群中计算 11 n + 3 11n+3 11n+3模指数。
Jarecki和Liu的工作与[16]是同时进行的。他们的协议只需要 5 n 5n 5n模块指数来计算恶意对手存在时的自适应集合交集,但是前提是在One-More Gap Diffie-Hellman(OMGDH)假设下。该假设认为即使DDH问题是容易的,One-More Diffie-Hellman问题也是困难的。
目前,最快的恶意两方PSI协议是由Pinkas、Rindal&Schoppmann设计的。他们不是基于Diffie-Hellman,而是基于有效的OT扩展或向量OLE。当集合的大小足够大时(例如: n > 2 2 0 n>2^20 n>220)时,[48]的协议是有效的,但它具有显著的固定成本,这使得它在较小的集合中效率低下。
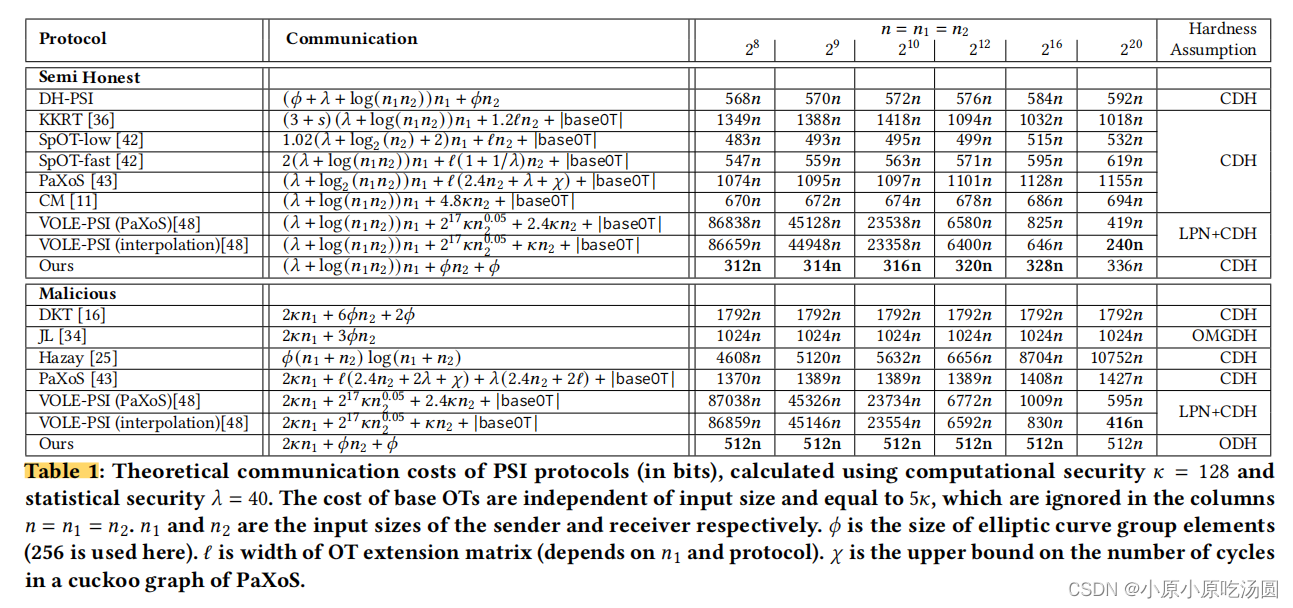
在表1中,我们展示了我们的协议与半诚实和恶意协议相比的理论通信复杂性。
1.2 结果总结
我们将展示如何将任何KA协议(具有伪随机消息和一个自然的不可塑属性)转换为一个PSI协议。
CDJ起点。我们的出发点是Cho、Dachman-Soled和Jarecki(CDJ)的方法。假设Alice持有项目 x 1 , . . . , x n x_1,...,x_n x1,...,xn且Bob有项目 y 1 , . . . , y n y_1,...,y_n y1,...,yn。每一方都将运行一个(恶意的)安全字符串相等测试协议的 n n n个实例,每个输入都有一个。考虑与项目 x i x_i xi对应的Alice的等式测试协议实例。她将如何将协议消息发送给Bob,以便(1)如果Bob也有 x i x_i xi,那么他将把它与这个实例(平等测试协议)关联,而不是其他实例,(2)如果Bob没有 x i x_i xi,他就不会知道Alice是否在运行一个与 x i x_i xi关联的实例。
CDJ的主要见解是在多项式中嵌入协议消息,其灵感源自Manulis,Pinkas和Poettering。对于等式测试协议的每一条消息,Alice将插值一个多项式 P P P,这样 P ( x i ) P(x_i) P(xi)等于第 i i i个等式测试实例的下一条消息。当Bob接收到这个多项式时,他可以在他的每个 y i y_i yi输入上计算它,响应每个输入,并将它们编码为他自己的多项式。重要的是,如果等测协议消息是足够随机的,那么多项式 P P P就隐藏了Alice的 x i x_i xi值。
我们的改进。我们在几个维度上改进了这个CDJ范例。(1)我们可以嵌入来自纯密钥协定(KA)协议的消息,而不是将来自恶意安全的字符串相等协议的消息嵌入到一个多项式中。(2)我们证明了一方可以避免将 n n n个KA消息嵌入到一个多项式中,而是只发送一个KA消息。这就大大减少了总的通信量。(3)我们简化了协议,以便使用理想的排列来代替理想的密码。
更详细地说,CDJ机制让各方运行字符串相等性测试的 n n n个实例。每个相等性测试将返回真或假,指示哪些项在交集中。我们观察到,成熟的等式测试对于CDJ来说太过分了。相反,让双方运行普通KA的 n n n个实例,根据他们的PSI输入嵌入到多项式中。每个KA实例都以一个输出键终止。如果Alice和Bob持有一个共同的项目,那么他们将有一个共同的密钥。如果Alice有一个Bob没有的项(反之亦然),我们将显示Alice计算了一个对Bob来说是随机的密钥。因此,对于PSI,双方只要简单地比较他们的KA输出集就足够了。
不仅关键协定协议在概念上比字符串相等测试协议更简单、更有效——它们也是不需要输入的。因此,KA协议具有它们的第一个协议消息可以为许多实例重用的属性。对于字符串相等式测试协议,这并不一定是这样的,因为当事方的输入字符串通常会被“嵌入”到第一个协议消息中。就PSI协议而言,这意味着我们的协议不需要第一个消息的一个𝑛次(对于𝑛项)的大多项式。相反,Alice只能发送一个KA协议消息,Bob计算 n n n个KA响应。
对于双消息KA协议(如Diffie-Hellman),第二条消息是伪随机的事实确保了多项式隐藏了输入集。通过在一些选定的地方添加随机语言调用,我们为模拟器提供了一个“钩子”来提取恶意各方的输入,从而产生一个恶意安全的PSI协议。
最后,由于技术原因,CDJ机制使用了一个理想的密码(使模拟器能够“编程”多项式的输出)。我们证明了一个更简单的理想排列就足够了。
Diffie-Hellman实例的表现。当我们的新的PSI范例用Diffie-Hellman KA实例化时,我们获得了迄今为止最有效的基于DH的PSI协议。对于恶意安全,我们要求oracle Diffie-Hellman(ODH)假设在循环群中保持。对于半诚实的安全性,我们只需要标准的CDH假设。
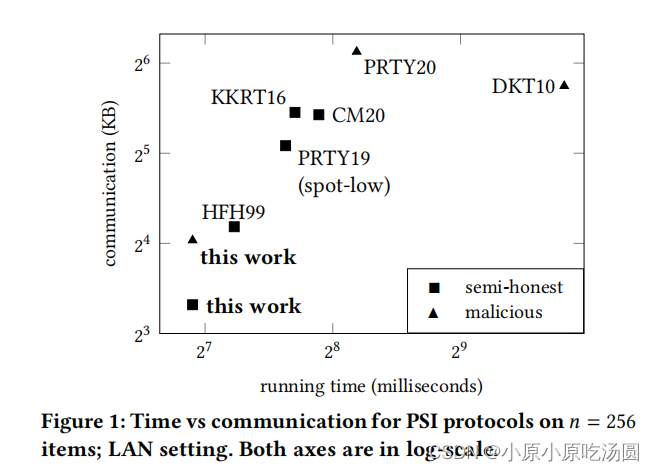
当集合大小很小(小于1000个项目)时,我们的协议比其他协议更快,通信使用更少——即使考虑半诚实协议和基于OT扩展的协议,这些协议在大集上更快。对于𝑛=256项目,我们的恶意协议比后者快18-30%(取决于网络速度),并且比后者(半诚实的)协议少使用10%的通信。我们的半诚实的变体比下一个最好的版本更少使用45%的通信。完整的比较见图1。
据我们所知,我们的研究是对20年前的经典DH-PSI协议的首次在通信方面进行改进的工作。我们降低了通信成本,同时将其从半诚实安全提升为恶意安全。经典的[29]半诚实DH-PSI协议需要总通信 2 n 2n 2n组元素加上 n n n个哈希;总计算量为 4 n 4n 4n基于变量的指数。在我们的协议中,总通信仅为𝑛+1组元素加上𝑛哈希;总计算是3𝑛固定基指数,2𝑛可变基指数,和𝑛多项式的二次多项式插值/多重计算。主要的基于DH的恶意PSI协议是由De Cristofaro,Kim和Tsudik设计的;它的总通信量是6𝑛组元素加上𝑛个哈希;总计算量为 2 n 2n 2n固定基指数和 4 n 4n 4n可变基指数。我们的恶意协议快了 30 30 30倍,使用的通信减少了80%。
2 准备工作
2.1 安全模型
安全的双方计算允许相互不信任的各方对其私有输入联合执行计算,而不透露除结果本身之外的任何附加信息。有两种敌对的模型通常被考虑。在半诚实模型中,假定敌手遵循协议,但可以试图从协议记录中学习信息。在恶意模型中,对手采用任意的多项式时间策略,并且在两种攻击类型的存在下都具有可行性。
2.2 PSI的功能
在图2中,我们正式描述了PSI功能,它允许双方在不透露任何额外信息的情况下计算它们所提供的数据集的交集。
请注意,该功能允许腐败的接收方拥有比敌手 ( n ) (n) (n)更多的输入项 ( n ′ ) ({n}') (n′)。这个属性反映了这样一个事实,即我们的协议不能严格地强制执行接收者所持有的项目的数量。这是PSI协议的一个共同特性,特别是由所有最快速的恶意安全的PSI协议[43,46,47]所共享的。我们将在第4.1节中讨论通过我们的协议实现的 n ′ {n}' n′和n之间的具体关系。
2.3 多项式运算
多项式插值和多点计算的一种常用实现是基于拉格朗日算法,需要 O ( n 2 ) O(n^2) O(n2)的域运算。62/5000
这种实现通常用于低次多项式。然而,当𝑛非常大时(例如: n = 2 20 n=2^{20} n=220),这个算法是完全不切实际的。在这项工作中,我们使用了速度更快的算法,它实现了计算复杂度 O ( n log 2 n ) O(n\log^2n) O(nlog2n)的算术运算。在高级思想上,这两个问题的算法都遵循分治的方法。特别是,在每次迭代后,这个问题被简化为两个半大小的问题。从两个小问题到一个完整的问题的解决方案的每个单独解决方案的组合都要花费 O ( n log n ) O(n \log n) O(nlogn)。因此,多项式插值和多点求值的总复杂度为 O ( n log 2 n ) O(n \log^2n) O(nlog2n)。
给定 X = x 1 , . . . , x n ⊆ F X={x_1,...,x_n}\subseteq F X=x1,...,xn⊆F和 Y = y 1 , . . . , y n ⊆ F Y={y_1,...,y_n}\subseteq F Y=y1,...,yn⊆F,我们使用 P = i n t e r p o l F ( ( x 1 , y 1 ) , . . . , ( x n , y n ) ) P=interpol_F({(x_1,y_1),...,(x_n,y_n)}) P=interpolF((x1,y1),...,(xn,yn))来表示多项式插值,该插值找到对所有 i ∈ [ n ] i\in [n] i∈[n]满足 P ( x i ) = y i P(x_i)=y_i P(xi)=yi的唯一 ( n − 1 ) (n-1) (n−1)次多项式 P P P。
2.4 理想排列
在理想的排列模型中,所有各方都有预言访问在 { 0 , 1 } n {\{0,1\}}^n {0,1}n随机排列 π \pi π和其逆 π − 1 \pi^{-1} π−1。我们写 π ± \pi^{\pm} π±是为了指代这对预言。在安全性证明中,模拟器回答了 π ± \pi^{\pm} π±的接口,这意味着它可以观察所有的查询并对响应进行编程。理想排列模型与理想密码模型相似,但较弱。一个理想的密码是一组理想的排列,每个密钥对应一个。
理想的排列假设最近在实际的MPC实现中流行起来,因为它允许加密操作基于固定密钥块密码上——即使用硬件加速的AES指令,而不计算AES密钥调度。理想的排列已被用来实现混乱电路和OT扩展的有效哈希函数。我们的工作需要一个理想的排列,支持密钥协定消息作为输入,因此我们的实现使用Rijndael-256,而不是AES(其块大小只有128)。我们注意到还有其他选项来实例化一个理想的排列。例如,使用海绵方法的对称关键结构都使用了一个有效的潜在理想排列。
3 密钥协定准备工作
我们从两轮密钥协定协议中构建PSI。一个2轮密钥协定协议KA有以下几个参数:
● K A . R KA.R KA.R是双方随机硬币的空间。
● K A . M KA.M KA.M是乙方可能收到的信息的空间。
● K A . K KA.K KA.K是可能的输出密钥的空间。
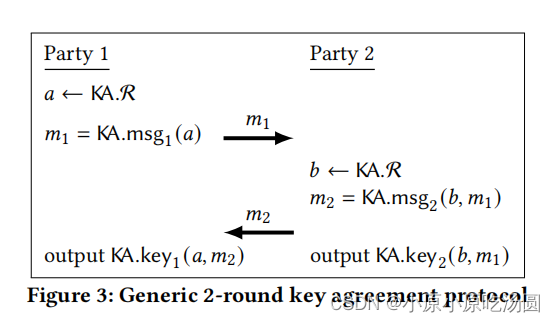
一个密钥协定协议包括以下算法: K A . m s g 1 KA.msg_1 KA.msg1, K A . m s g 2 KA.msg_2 KA.msg2, K A . k e y 1 KA.key_1 KA.key1, K A . k e y 2 KA.key_2 KA.key2。这些对应于一个如图3所示的交互式密钥协定协议。
在一些2轮密钥协定协议中,第二个消息 m 2 m2 m2不依赖于第一个消息 m 1 m1 m1,我们可以写 m 2 = K A . m s g 2 ( b ) m2=KA.msg_2(b) m2=KA.msg2(b),而不是 K A . m s g 2 ( b , m 1 ) KA.msg_2(b,m_1) KA.msg2(b,m1)。在这些情况下, m 1 m1 m1和 m 2 m2 m2可以同时发送(或以任何一种顺序发送),我们说密钥协定协议是一轮的。
3.1 安全属性
我们的PSI协议的不同实例化需要一个密钥协定协议的以下安全属性。请注意,定义3.4和强统一KA(SU-KA)是相似的,但我们的定义是专门用于1轮KA的。
定义3.1.如果在如图3所示的诚实执行时,双方给出相同的输出,则KA方案是正确的。换句话说,对于所有的 a , b ∈ K A . R a,b\in KA.R a,b∈KA.R: K A . k e y 1 ( a , K A . m s g 2 ( b , K A . m s g 1 ( a ) ) ) = K A . k e y 2 ( b , K A . m s g 1 ( a ) ) KA.key_1(a,KA.msg_2(b,KA.msg_1(a)))=KA.key_2(b,KA.msg_1(a)) KA.key1(a,KA.msg2(b,KA.msg1(a)))=KA.key2(b,KA.msg1(a))
定义3.2.如果以下分布无法区分,则KA方案对窃听者是安全的:
定义3.3.如果KA方案是安全的(在定义3.2的意义上),那么它对于仅能访问 K A . k e y 1 ( a , ⋅ ) KA.key_1(a,·) KA.key1(a,⋅),而不能访问 m 2 m_2 m2的窃听者来说就是不可延展的。形式上,下面的分许对于每个从不在输入 m 2 m_2 m2上查询其预言的 P P T A PPT A PPTA是不可区分的。
定义3.4.如果 m 2 m2 m2与随机消息无法区分,则KA方案具有伪随机的第二条消息,即使对那些反向选择 m 1 m1 m1的人也是如此。形式上,下面的分布对于所有的 P P T A PPT A PPTA是无法区分的。
3.2 Diffie-Hellman实例
经典的Diffie-Hellman密钥协定协议是一个一轮的KA协议(这意味着这两个消息可以同时发送)。它由一个 q q q阶的循环群 G = < g > G=<g> G=<g>参数化,定义为:
● K A . R = Z q KA.R=Z_q KA.R=Zq(私有随机空间)
● K A . M = G KA.M=G KA.M=G(第二方协议信息的空间)
● K A . m s g 1 ( a ) = g a KA.msg_1(a)=g^a KA.msg1(a)=ga
● K A . m s g 2 ( b ) = g b KA.msg_2(b)=g^b KA.msg2(b)=gb
在这项工作中,我们考虑了DH的哈希变量。在随机预言模型中,它在computational Diffie-Hellman(CDH)假设下是安全的。让 H : G → { 0 , 1 } l H:G\to {\{0,1\}}^l H:G→{0,1}l是一个随机预言,则有:
● K A . κ = { 0 , 1 } l KA.\kappa ={\{0,1\}}^l KA.κ={0,1}l(输出密钥的空间)
● K A . k e y 1 ( a , g b ) = H ( ( g b ) a ) KA.key_1(a,g^b)=H((g^b)^a) KA.key1(a,gb)=H((gb)a)
● K A . k e y 2 ( b , g a ) = H ( ( g a ) b ) KA.key_2(b,g^a)=H((g^a)^b) KA.key2(b,ga)=H((ga)b)
Elligator DHKA.DHKA的现代应用使用椭圆曲线来表示底层的循环组,因为它们的大小紧凑化(例如,对于 k k k的安全位,组元素大约表示为 2 k 2k 2k位)。然而,椭圆曲线元素的编码相当明显,并且可以很容易地与均匀分布的字符串进行区分。我们的PSI协议要求KA协议消息(特别是 m 2 m2 m2)作为字符串是伪随机的。
在[6]中,Bernstein等人明确地考虑了对椭圆曲线元素进行编码的问题,因此产生的Diffie-Hellman协议具有伪随机消息(视为字符串)。形式上,它们定义了一种称为elligator的编码机制,具有以下属性:
●这里有有效的编码/解码函数dec和enc,其中 i m ( e n c ) ⊆ { 0 , 1 } t im(enc)\subseteq {\{0,1\}}^t im(enc)⊆{0,1}t是一组字符串, i m ( d e c ) ⊆ ε im(dec)\subseteq \varepsilon im(dec)⊆ε是椭圆曲线点的子集。
● i m ( e n c ) im(enc) im(enc)的大小非常接近于 2 t 2t 2t,因此编码上的均匀分布与{{0,1}}^t上的均匀分布难以区分。
● i m ( e n c ) im(enc) im(enc)的大小是椭圆曲线大小的常数分数(通常接近 1 / 2 1/2 1/2)。
●可以有效地测试 i m ( e n c ) im(enc) im(enc)中的成员资格(也包括 i m ( d e c ) im(dec) im(dec)中的)。
在为Edwards曲线定义了这种弹性编码方法后,Bernstein等人提出对Diffie-Hellman密钥协定协议进行如下修改:
● K A . R = { r ∈ Z q ∣ g r ∈ i m ( d e c ) } KA.R=\{r\in Z_q|g^r\in im(dec)\} KA.R={r∈Zq∣gr∈im(dec)}.
● K A . M KA.M KA.M={{0,1}}^t
● K A . m s g 1 ( a ) = e n c ( g a ) KA.msg_1(a)=enc(g^a) KA.msg1(a)=enc(ga)
● K A . m s g 2 ( b ) = e n c ( g b ) KA.msg_2(b)=enc(g^b) KA.msg2(b)=enc(gb)
● K A . k e y 1 ( a , s b ) = H ( d e c ( s b ) a ) KA.key_1(a,s_b)=H(dec(s_b)^a) KA.key1(a,sb)=H(dec(sb)a)
● K A . k e y 2 ( b , s a ) = H ( d e c ( s a ) b ) KA.key_2(b,s_a)=H(dec(s_a)^b) KA.key2(b,sa)=H(dec(sa)b)
换句话说,双方为他们的随机性设定了条件,即总是在曲线的“弹性子集” i m ( d e c ) im(dec) im(dec)中采样一个点。在实际中,每一方都会重复采样一个指数 r ← Z q r\gets Z_q r←Zq,然后重试,直到在弹性子集中找到一个。由于 ∣ i m ( d e c ) ∣ / ∣ ε ∣ |im(dec)|/|\varepsilon| ∣im(dec)∣/∣ε∣是一个常量,所以在成功到达 i m ( d e c ) im(dec) im(dec)之前只需要恒定数量的试验。此外,DHKA的具体安全性仅被一个很小的常数因子所降低。
由于弹性编码的期望特性,协议消息在 i m ( e n c ) im(enc) im(enc)中是一致的,因此在 { 0 , 1 } t {\{0,1\}}^t {0,1}t中是伪随机的。
安全属性。哈希DHKA对窃听者(定义3.2)的安全性是标准的,并遵循CDH假设。
elligator-DHKA协议的“伪随机第二消息”属性(定义3.4)遵循上面讨论的elligator的属性。请注意,在DHKA中, m 2 m2 m2并不依赖于 m 1 m1 m1,所以对手在定义3.4中选择 m 1 m1 m1的能力是不恰当的。最后,哈希DHKA的“不可塑”属性(定义3.3)等价于Abdalla,Bellare和Rogaway提出的预言DH(ODH)假设。粗略地说,ODH的假设是:在对 X ↦ H ( X a ) X\mapsto H(X^a) X↦H(Xa)的预言存在的情况下, g a g^a ga, g b g^b gb和 H ( g a b ) H(g^{ab}) H(gab)与随机值是无法区分的,只要区分器不在 g b g^b gb上查询该预言。这里的 H H H是哈希DHKA中使用的哈希函数/随机预言。在[2]中,当 H H H是一个随机预言时,ODH假设在一般群模型中成立。
4 来自密钥协定的恶意PSI
在本节中,我们将介绍我们主要的结果,一个恶意的两方PSI协议。我们的协议需要以下构建模块:
●一个两轮KA协议。 K A . M KA.M KA.M是可能的协议消息的空间。对于一些有限域 F F F,我们需要 K A . M = F KA.M=F KA.M=F。并且 K A KA KA协议在这个域中有伪随机消息。我们还要求 K A KA KA协议在定义3.3的意义上是不可塑的。
●各方可以获得在同一个域 F F F上定义的理想排列 Π \Pi Π, Π − 1 \Pi^{-1} Π−1。我们书写 Π ± \Pi^{\pm} Π±来集体引用这两个函数 Π \Pi Π, Π − 1 \Pi^{-1} Π−1。各方也可以获得随机预言 H 1 H_1 H1, H 2 H_2 H2。
作为一个具体的例子,我们可以选择带有弹性编码的哈希DHKA(见第3.2节),它的协议消息在 { 0 , 1 } l {\{0,1\}}^l {0,1}l中是伪随机的,然后将 F F F设置为字段 G F ( 2 l ) GF(2^l) GF(2l)。在ODH假设下,哈希DHKA也是不可延展的。我们将在第5节中给出更多关于用Diffie-Hellman来实例化我们的协议的细节。
协议概述。按照第1节中给出的概述,发送方发送第一个 K A KA KA消息。直观地说,接收器准备了一个多项式 P P P,这样 P ( y i ) P(y_i) P(yi)是它所选择的 K A KA KA响应,对于其集中的每个 y i y_i yi。如果KA响应是伪随机的,那么多项式 P P P隐藏了 y i y_i yi值的恒等式。
然而,由于技术原因,我们让接收器准备一个多项式,形式如: P ( H 1 ( y i ) ) = Π − 1 ( m i ) P(H_1(y_i))=\Pi^{-1}(m_i) P(H1(yi))=Π−1(mi),其中 H 1 H_1 H1是一个随机预言, Π \Pi Π是一个理想排列,而 m i m_i mi是一个KA响应。随机预言 H 1 H_1 H1的存在有助于模拟器从腐败的接收方(从观察它的 H 1 H_1 H1-查询中提取)获取消息。理想排列的存在帮助模拟器(针对两个腐败的双方),通过编程 Π \Pi Π输出模拟器选择的KA消息。
最后,对于集合中的每个 x i x_i xi,发送方可以将 Π ( P ( H 1 ( x i ) ) ) \Pi(P(H_1(x_i))) Π(P(H1(xi)))解释为一个KA响应,并计算相应的KA输出 k i k_i ki。对于每个 x i x_i xi,发送方将向接收方发送 H 2 ( x i , k i ) H_2(x_i,k_i) H2(xi,ki)。这个随机预言的存在再次帮助模拟器从腐败的发送者中提取信息。
我们在图4中正式描述了该协议。 i n t e r p o l F interpol_F interpolF表示域 F F F上的多项式插值,如第2.3节所述。
在给出证明之前,我们首先概述了模拟器的主要思想。当模拟器看到敌手提供的集合 K K K时,它需要提取一组项来“解释” K K K对诚实方的影响。 K K K的元素应该有 H 2 ( x i , k i ) H_2(x_i,k_i) H2(xi,ki)的形式,其中 k i k_i ki是项目 x i x_i xi的“正确”KA输出。模拟器观察所有对 H 2 H_2 H2的查询,这样它就可以看到哪些 H 2 − H_2- H2−输出被放入 K K K中——但是模拟器如何检查某些 k i k_i ki是与项目 x i x_i xi对应的“正确的”KA输出呢?为了做到这一点,我们让模拟器运行程序 Π \Pi Π,这样 Π \Pi Π的每个输出都是一个KA消息,并知道其随机性。现在,对于任何𝑥,使用它与 Π ( P ( H 1 ( x ) ) ) \Pi(P(H_1(x))) Π(P(H1(x)))关联的KA随机性,模拟器都可以计算相应的KA输出,。
证明。我们首先描述模拟器的行为。
●模拟器诚实地扮演了随机预言 H 2 H_2 H2的角色。对于敌手做出的每一个查询 H 2 ( x , k ) H_2(x,k) H2(x,k),模拟器都会记录在集合 O 2 O_2 O2中的输入-输出元组 ( x , k , H 2 ( x , k ) ) (x,k,H_2(x,k)) (x,k,H2(x,k))。
●对于在发送消息 m m m后对 Π ( f ) \Pi(f) Π(f)形式进行的每个查询,模拟器选择一个随机的 b f ← K A . R b_f\gets KA.R bf←KA.R,并模拟 K A . m s g 2 ( b f , m ) KA.msg_2(b_f,m) KA.msg2(bf,m)作为 Π ( f ) \Pi(f) Π(f)的输出。
●在步骤4中,模拟器发送一个均匀的多项式 P P P。
●当在步骤6中接收到𝐾后,模拟器定义了该集合: X ~ = { x ∣ ∃ k ′ : ( x , K A . k e y 2 ( b p ( H 1 ( x ) ) , m ) , k ′ ) ∈ O 2 a n d k ′ ∈ K } \tilde{X}=\{x\mid \exist{k}':(x,KA.key_2(b_{p(H_1(x))},m),{k}')\in O^2 \quad and \quad {k}' \in K \} X~={x∣∃k′:(x,KA.key2(bp(H1(x)),m),k′)∈O2andk′∈K} ,并将 X ~ \tilde{X} X~发送到理想的PSI功能(这使诚实的接收器获得输出 x ~ ∩ Y \tilde{x} \cap Y x~∩Y)。
我们通过以下的混合序列证明了这个模拟与真实的交互是无法区分的。
混合0:真正的交互,与接收方通过输入 Y Y Y诚实地运行,并根据协议规范将其输出提供给环境。
混合1:与之前的混合相同,除了如何模拟 Π ± \Pi^{\pm} Π±。对于 Π \Pi Π(关于 Π − 1 \Pi{-1} Π−1)的查询是新的如果以前从未做过。并且它的值不是由以前对 Π − 1 \Pi^{-1} Π−1的查询决定的, Π \Pi Π和 Π − 1 \Pi^{-1} Π−1是互逆的。在这个混合版本中,所有对 Π \Pi Π和 Π − 1 \Pi^{-1} Π−1的新查询(由敌手或诚实方)都以统一的随机响应进行回答。如果这导致 Π \Pi Π或 Π − 1 \Pi^{-1} Π−1重复一个输出,则交互将中止。这种变化与标准的排列转换引理没有什么区别。
混合2:与之前的混合版本相同,除了 P P P是如何生成的。在步骤3中,通过形式为 Π − 1 ( K A . m s g 2 ( b i , m ) ) \Pi^{-1}(KA.msg_2(b_i,m)) Π−1(KA.msg2(bi,m))的点进行插值来生成 P P P。在这个混合版本中,如果这些对 Π − 1 \Pi^{-1} Π−1的查询不是新的,我们将中止。例如,如果 K A . m s g 2 ( b i , m ) KA.msg_2(b_i,m) KA.msg2(bi,m)以前作为对手对 Π − 1 \Pi^{-1} Π−1的查询或作为对手对 Π \Pi Π的查询的输出发生。
如果 K A . m s g 2 ( b i , m ) KA.msg_2(b_i,m) KA.msg2(bi,m)项是独立且一致随机的,那么当对手进行 q q q预言查询时,这个中止将以 n q / ∣ F ∣ nq/\mid F\mid nq/∣F∣限制的概率发生。根据KA格式的伪随机性质,每个 K A . m s g 2 ( b i , m ) KA.msg_2(b_i,m) KA.msg2(bi,m)与随机性难以区分,因此中止概率与 n q / ∣ F ∣ nq/\mid F\mid nq/∣F∣十分的接近。不管怎样,这个概率都是十分接近的,所以混合也是无法区分的。
现在在不中止的条件下,我们有了每个 Π − 1 ( K A . m s g 2 ( . . . ) ) \Pi^{-1}(KA.msg_2(...)) Π−1(KA.msg2(...))都是一个新的和平均的值。因此, P P P作为一个均匀的多项式分布,与 y i y_i yi的值无关。这种交互作用与我们相同,我们首先选择一个统一多项式 P P P,然后为每个 y i ∈ Y y_i \in Y yi∈Y编程 Π ( P ( H 1 ( y i ) ) ) = K A . m s g 2 ( b i , m ) \Pi(P(H_1(y_i)))=KA.msg_2(b_i,m) Π(P(H1(yi)))=KA.msg2(bi,m)(如果 Π \Pi Π已经在这一点上编程,则中止)。
混合3:与之前的混合版本相同,除了如何模拟 Π \Pi Π。对于在敌手发送 m m m之后进行的每一个新的查询 Π ( f ) \Pi(f) Π(f),样例 b f ← K A . R b_f\gets KA.R bf←KA.R并使用 K A . m s g 2 ( b f , m ) KA.msg_2(b_f,m) KA.msg2(bf,m)响应(而不是以统一的结果响应)。这种变化由于KA的伪随机性无法区分。注意,对于 y i ∈ Y y_i\in Y yi∈Y,我们已经用这种方式模拟了 Π ( P ( H 1 ( y i ) ) ) \Pi(P(H_1(y_i))) Π(P(H1(yi))),但使用不同的变量名(随机 b i b_i bi而不是对于 P ( H 1 ( y i ) ) P(H_1(y_i)) P(H1(yi))的 b f b_f bf)。如果我们将随机性 b i b_i bi对于 ( y i ∈ Y ) (y_i\in Y) (yi∈Y)重命名为 b p ( H 1 ( y i ) ) b_p(H_1(y_i)) bp(H1(yi)),那么我们将以相同的方式对所有输入编程 Π \Pi Π,而对于 Y Y Y的元素没有特殊情况。这样做,诚实方的产出可以通过以下方式计算: { y i ∈ Y ∣ H 2 ( y i , K A . k e y 2 ( b P ( H 1 ( y i ) ) , m ) ) ∈ K } \{y_i\in Y\mid H_2(y_i,KA.key_2(b_{P(H_1(y_i))},m))\in K\} {yi∈Y∣H2(yi,KA.key2(bP(H1(yi)),m))∈K}
混合4:诚实的接收器查询𝐻2以确定它的最终输出(在上面的表达式中)。在这个混合版本中,如果其中一个 H 2 H_2 H2查询是新的(这意味着敌手没有进行该查询),而结果是在 K K K中,我们就会中止。一个新查询的输出成为 K K K元素的概率是 ∣ K ∣ / ∣ F ∣ = n / ∣ F ∣ \mid K\mid /\mid F \mid=n/\mid F\mid ∣K∣/∣F∣=n/∣F∣,这可以忽略不计。因此,这种变化是无法区分的。
假设最终的混合保持了前面描述的列表 O 2 O_2 O2——即, ( x , k , k ′ ) ∈ O 2 (x,k,{k}')\in O_2 (x,k,k′)∈O2意味着敌手查询了 H 2 ( x , k ) H_2(x,k) H2(x,k)并得到了一个结果 k ′ {k}' k′。由于接收方只“识别”敌手已经向 H 2 H_2 H2查询的值,所以这个最终的混合值与接收方输出的计算结果相同: { y i ∈ Y ∣ ∃ k ′ : ( y i , K A . k e y 2 ( b P ( H 1 ( y i ) ) , m ) , k ′ ) ∈ O 2 a n d k ′ ∈ K } \{y_i \in Y \mid \exist {k}':(y_i,KA.key_2(b_{P(H_1(y_i))},m),{k}')\in O_2 \quad and \quad {k}'\in K \} {yi∈Y∣∃k′:(yi,KA.key2(bP(H1(yi)),m),k′)∈O2andk′∈K}
但这在逻辑上相当于: { Y ∩ { x ∣ ∃ k ′ : ( x , K A . k e y 2 ( b P ( H 1 ( x ) ) , m ) , k ′ ) ∈ O 2 a n d k ′ ∈ K } } → x ~ \{Y \cap \{x \mid \exist {k}':(x,KA.key_2(b_{P(H_1(x))},m),{k}')\in O_2\quad and \quad {k}'\in K\} \} \to \tilde{x} {Y∩{x∣∃k′:(x,KA.key2(bP(H1(x)),m),k′)∈O2andk′∈K}}→x~这里的 x ~ \tilde{x} x~是模拟器可以定义的集合。因此,这种混合作用与前面定义的模拟器的理想交互是相同的。
引理 4.2.图4的协议对于恶意接收方是UC-安全的,如果KA是不可延展的,则有 ∣ K A . K ∣ ≥ 2 k \mid KA.K \mid \ge 2^k ∣KA.K∣≥2k, H 1 H_1 H1和 H 2 H_2 H2是随机预言,且 Π ± \Pi^{\pm} Π±是一个理想排列。
在给出证明之前,我们首先概述了模拟器的主要思想。当敌手给出多项式 P P P时,模拟器的工作是提取一个集合 Y ~ \tilde{Y} Y~,它可以发送到理想的功能。然后,在学习了 X ∩ Y ~ X \cap \tilde{Y} X∩Y~之后,它适当地模拟了消息 K K K。直观地说,我们想要区分接收者参与的KA实例和接收者作为窃听者的KA实例。前一个实例将对应于 Y ~ \tilde{Y} Y~的项,而后一个实例将有助于生成看起来是随机的KA输出(和K的元素)。
诚实的发送方将 Π ( P ( H 1 ( x ) ) ) \Pi(P(H_1(x))) Π(P(H1(x)))解释为每个 x ∈ X x\in X x∈X的KA消息。接收器只“控制”这个值,如果:(1)它查询到 H 1 ( x ) H_1(x) H1(x);(2)它对 Π − 1 \Pi^{-1} Π−1进行了一个向后查询,结果得到了值 P ( H 1 ( x ) ) P(H_1(x)) P(H1(x))。另一方面,如果对手首先选择 P ( H 1 ( x ) ) P(H_1(x)) P(H1(x)),然后只在 Π ( \Pi ( Π(P(H_1(x)) ) ) )上进行正向查询,那么直观上它将对结果值没有控制。模拟器观察对 Π ± \Pi^{\pm} Π±和 H 1 H_1 H1的所有查询,因此可以使用这些标准来识别哪些KA实例将给出接收器可以识别的输出。所有其他的KA输出都可以安全地用随机来替换。
我们提请读者注意这个证据中的两个微妙之处:假设敌手查询 Π \Pi Π以获得一些KA消息 m ∗ m^* m∗。由于(直观上)敌手无法控制 m ∗ m^* m∗,我们想表明相应的 K A . k e y ( m ∗ ) KA.key(m^*) KA.key(m∗)(这里轻微滥用符号)看起来是随机的。但是假设对手程序 P P P,使 Π ( P ( H 1 ( y ) ) ) = m ∗ \Pi(P(H_1(y)))=m^* Π(P(H1(y)))=m∗和 Π ( P ( H 1 ( y ′ ) ) ) = m ∗ + 1 \Pi(P(H_1({y}')))=m^*+1 Π(P(H1(y′)))=m∗+1。如果发送方同时具有输入 y y y和 y ′ {y}' y′,那么她将计算并发送 K A . k e y ( m ∗ ) KA.key(m^*) KA.key(m∗)和 K A . k e y ( m ∗ + 1 ) KA.key(m^*+1) KA.key(m∗+1)。即使存在后者,前者的KA输出看起来也是随机的吗?如果KA协议在定义3.3的意义上是不可延展性的,那么就的确如此。
另一个微妙之处在于,接收器可以选择它的多项式 P P P来进行“碰撞”,即 P ( H 1 ( y ) ) = P ( H 1 ( y ′ ) ) P(H_1(y))=P(H_1({y}')) P(H1(y))=P(H1(y′))。这本身不是一个问题或攻击,但它意味着证明中的混合体必须仔细地构建结构。证明的目的是证明发送者形式 H 2 ( x i , K A . k e y ( Π ( P ( H 1 ( x i ) ) ) ) ) H_2(x_i,KA.key(\Pi (P(H_1(x_i))))) H2(xi,KA.key(Π(P(H1(xi)))))的消息可以用随机值替换,对于所有不在交集中的 x i x_i xi。但是混合的序列并不能用一次随机的一个值来代替这些真实的值。相反,我们一次替换一个 Π ( P ( H 1 ( ⋅ ) ) ) \Pi(P(H_1(\cdot))) Π(P(H1(⋅)))输出,使用由模拟器选择的KA的消息。然后我们可以论证 K A . k e y ( Π ( P ( H 1 ( x i ) ) ) ) KA.key(\Pi (P(H_1(x_i)))) KA.key(Π(P(H1(xi))))与随机的 x i x_i xi值具有相同的 P ( H 1 ( x i ) ) P(H_1(x_i)) P(H1(xi))。
证明。我们首先正式地描述了模拟器的行为:
●该模拟器诚实地发挥了随机预言 H 1 H_1 H1和理想排列 Π ± \Pi^{\pm} Π±的作用。对于敌手进行的每个查询 H 1 ( y ) H_1(y) H1(y),在集合 O 1 O_1 O1中记录 y y y。对于每个查询 Π − 1 ( m ) = f \Pi^{-1}(m)=f Π−1(m)=f,其中没有之前对形式 Π ( f ) = m \Pi(f)=m Π(f)=m的查询,在集合 O Π O_{\Pi} OΠ中记录 f f f。
●模拟器诚实地运行步骤1-2。
●在步骤4中接收到𝑃后,模拟器定义该集合 Y ~ = { y ∣ y ∈ O 1 a n d P ( H 1 ( y ) ) ∈ O Π } \tilde{Y} =\{y \mid y \in O_1 \quad and \quad P(H_1(y)) \in O_{\Pi} \} Y~={y∣y∈O1andP(H1(y))∈OΠ},并发送 Y ~ \tilde{Y} Y~到理想的PSI功能。
●在从功能接收到输出 Z = X ∩ Y ~ Z=X \cap \tilde{Y} Z=X∩Y~后,模拟器为每个 z ∈ Z z \in Z z∈Z计算 k z = K A . k e y 1 ( a , Π ( P ( H 1 ( z ) ) ) ) k_z=KA.key_1(a,\Pi (P(H_1(z)))) kz=KA.key1(a,Π(P(H1(z))))。定义 K = { H 2 ( z , k z ) ∣ z ∈ Z } K=\{H_2(z,k_z) \mid z \in Z\} K={H2(z,kz)∣z∈Z},然后不断向 K K K添加均匀的随机值,直到 ∣ K ∣ = ∣ X ∣ \mid K \mid=\mid X \mid ∣K∣=∣X∣。模拟器最终将这个 K K K发送给敌手。
我们通过以下的混合序列证明了这个模拟与真实的插入是无法区分的。
混合0:真正的交互,与发送者诚实地运行在输入 X X X上。特别是,协议消息𝐾的生成方式如下: K = { H 2 ( x , K A . k e y 1 ( a , Π ( P ( H 1 ( x ) ) ) ) ) ∣ x ∈ X } K=\{H_2(x,KA.key_1(a,\Pi (P(H_1(x)))))\mid x \in X\} K={H2(x,KA.key1(a,Π(P(H1(x)))))∣x∈X}。列表 O 1 O_1 O1和 O 2 O_2 O2也保持一样,如上所示。
混合1:与之前的混合相同,除了在步骤5中,如果存在 x ∈ X x\in X x∈X, x ∉ O 1 x \notin O_1 x∈/O1和 P ( H 1 ( x ) ) ∈ O Π P(H_1(x))\in O_{\Pi} P(H1(x))∈OΠ,则交互中止。换句话说,对手每个查询的 H 1 ( x ) H_1(x) H1(x)和 P ( H 1 ( x ) ) P(H_1(x)) P(H1(x))是它之前从 Π − 1 \Pi^{-1} Π−1接收到的输出值。
这足以表明这种中止的概率可以忽略不计。对于任何 f ∈ O Π f\in O_{\Pi} f∈OΠ,多项式方程 P ( ⋅ ) = f P(\cdot)=f P(⋅)=f最多有 n n n解,因为 P P P是一个 n n n次的多项式,而不是零多项式(这意味着 P P P是一个常数多项式,发送方已经在第四步中止)。由于 H 1 ( x ) H_1(x) H1(x)是一个以前从未做过的新查询(直到模拟发送方完成),它在 F F F中均匀分布,因此最多以 n / ∣ F ∣ n/ \mid F\mid n/∣F∣的概率满足 P ( H 1 ( x ) ) = f P(H_1(x))=f P(H1(x))=f。假设敌手对其预言总共进行了 q q q次查询。通过 x ∈ X x\in X x∈X的所有 n n n选择和 f ∈ O Π f\in O_{\Pi} f∈OΠ的 q q q选择的并界,该事件的总概率为 n 2 q / ∣ F ∣ n^2q/\mid F \mid n2q/∣F∣,可以忽略不计。
混合 ( 2 , i ) (2,i) (2,i),对于 i ∈ [ q ] i \in [q] i∈[q]:与前一个混合版本相同,除了以下更改。对于表单 Π ( f ) = m \Pi(f)=m Π(f)=m的第一个 i i i查询,其中之前没有对 Π − 1 ( m ) \Pi^{-1}(m) Π−1(m)的查询,请将 f f f添加到集合 S i S_i Si中。请注意, S i S_i Si和 O Π O_{\Pi} OΠ必然是不相交的(基于是否先查询 Π \Pi Π和 Π − 1 \Pi^{-1} Π−1)。直观地说, S i S_i Si是对手无法控制的第一个 i i i Π − \Pi- Π−输出(在协议中解释为KA协议消息)。然后计算 K K K代替: K = { H 2 ( x , K A . k e y 1 ( a , Π ( P ( H 1 ( x ) ) ) ) ) ∣ x ∈ X a n d P ( H 1 ( x ) ) ∉ S i } K=\{H_2(x,KA.key_1(a,\Pi(P(H_1(x))))) \mid x\in X\quad and \quad P(H_1(x))\notin S_i\} K={H2(x,KA.key1(a,Π(P(H1(x)))))∣x∈XandP(H1(x))∈/Si},然后在 K K K中添加均匀的随机元素,直到 ∣ K ∣ = n \mid K\mid =n ∣K∣=n。注意,可能有许多 x x x值给出相同的P(H_1(x))输出,因此在混合 ( 2 , i ) (2,i) (2,i)和 ( 2 , i + 1 ) (2,i+1) (2,i+1)之间可能有许多不同处理的 x x x的值。应该清楚的是,混合 ( 2 , 0 ) (2,0) (2,0)与混合2是相同的,因为 S 0 = ∅ S_0=\emptyset S0=∅和新的条件总是真的。在引理4.3中,我们证明混合 ( 2 , i ) (2,i) (2,i)和 ( 2 , i + 1 ) (2,i+1) (2,i+1)是不可区分的。
混合3:为了清晰起见,我们重写了混合 ( 2 , q ) (2,q) (2,q)。在这个混合中,交互中已知的每个 Π ( f ) = m \Pi(f)=m Π(f)=m都用 S q S_q Sq(在初始 Π \Pi Π查询中已知的)或 O Π O_{\Pi} OΠ(初始 Π − 1 \Pi^{-1} Π−1查询中已知的)表示。换句话说,这两个集合构成了所有已知的 Π ( f ) = m \Pi(f)=m Π(f)=m点的一个分区。
让我们考虑在这个混合中是如何计算集合𝐾的。条件 P ( H 1 ( x ) ) ∉ S q P(H_1(x))\notin S_q P(H1(x))∈/Sq等价于 P ( H 1 ( x ) ) ∈ O Π P(H_1(x))\in O_{\Pi} P(H1(x))∈OΠ,意味着我们可以写: K = { H 2 ( x , K A . k e y 1 ( a , Π ( P ( H 1 ( x ) ) ) ) ) ∣ x ∈ X a n d P ( H 1 ( x ) ) ∈ O Π } K=\{H_2(x,KA.key_1(a,\Pi(P(H_1(x))))) \mid x \in X\quad and \quad P(H_1(x))\in O_{\Pi}\} K={H2(x,KA.key1(a,Π(P(H1(x)))))∣x∈XandP(H1(x))∈OΠ}(用随机值填充)。
回想一下,如果有任何 x ∉ O 1 x \notin O_1 x∈/O1,但 P ( H 1 ( x ) ) ∈ O Π P(H_1(x))\in O_{\Pi} P(H1(x))∈OΠ,则交互中止。换句话说,即使在相互作用中达到这一点, P ( H 1 ( x ) ) ∈ O Π P(H_1(x))\in O_{\Pi} P(H1(x))∈OΠ也意味着 x ∈ O 1 x \in O_1 x∈O1。因此,我们可以进一步重写 K K K的定义为: K = { H 2 ( x , K A . k e y 1 ( a , Π ( P ( H 1 ( x ) ) ) ) ) ∣ x ∈ X ∩ O 1 a n d P ( H 1 ( x ) ) ∈ O Π } K=\{H_2(x,KA.key_1(a,\Pi(P(H_1(x)))))\mid x\in X\cap O_1 \quad and \quad P(H_1(x))\in O_{\Pi}\} K={H2(x,KA.key1(a,Π(P(H1(x)))))∣x∈X∩O1andP(H1(x))∈OΠ}。
现在,假设我们定义了 Y ~ = { y ∣ y ∈ O 1 a n d P ( H 1 ( y ) ) ∈ O Π } \tilde{Y}=\{y \mid y\in O_1 \quad and \quad P(H_1(y))\in O_{\Pi}\} Y~={y∣y∈O1andP(H1(y))∈OΠ}。然后 K K K可以被重写成等价的形式: K = { H 2 ( x , K A . k e y 1 ( a , Π ( P ( H 1 ( x ) ) ) ) ) ∣ x ∈ X ∩ Y ~ } K=\{H_2(x,KA.key_1(a,\Pi(P(H_1(x))))) \mid x \in X\cap \tilde{Y}\} K={H2(x,KA.key1(a,Π(P(H1(x)))))∣x∈X∩Y~}。
在这种形式下,现在很清楚,混合对应于理想相互作用的行为。也就是说,模拟器计算 Y ~ \tilde{Y} Y~,然后仅根据 Z = X ∩ Y ~ Z=X\cap \tilde{Y} Z=X∩Y~的内容,即其功能的输出来计算 K K K。
引理4.3.如果KA协议是不可塑的(定义3.3)且 ∣ K A . K ∣ ≥ 2 k \mid KA.K \mid \ge 2^k ∣KA.K∣≥2k,则混合 ( 2 , i − 1 ) (2,i-1) (2,i−1)和 ( 2 , i ) (2,i) (2,i)是不可区分的。
证明。混合仅在下面的几个方式的时候不同:混合 ( 2 , i ) (2,i) (2,i)用随机值替换 K A . k e y 1 ( a , Π ( f ∗ ) ) KA.key_1(a,\Pi(f^*)) KA.key1(a,Π(f∗)),如果 f ∗ f^* f∗是对 Π \Pi Π的第 i i i次查询(之前没有相应的 Π − 1 \Pi^{-1} Π−1查询)。
回想一下,在定义KA的不可延展性的游戏中,区分器接收 ( m 1 = K A . m s g 1 ( a ) , m 2 , k ) (m_1=KA.msg_1(a),m_2,k) (m1=KA.msg1(a),m2,k),也可以访问 K ( ⋅ ) = K A . k e y 1 ( a , ⋅ ) K(\cdot)=KA.key_1(a,\cdot) K(⋅)=KA.key1(a,⋅)的预言,它不能在 m 2 m_2 m2上查询。下面是一个简化算法,它是一个区分非延展性游戏的算法: R K ( m 1 , m 2 , k ) R^K(m_1,m_2,k) RK(m1,m2,k):
●运行混合 ( 2 , i − 1 ) (2,i-1) (2,i−1)反抗敌手,使用 m 1 m_1 m1作为PSI协议消息 m m m。
●按照描述的维持集合 S i − 1 S_{i-1} Si−1。对于对 Π \Pi Π的第 i i i次查询(将被添加到 S i S_i Si的值),让 f ∗ f^* f∗表示输入,并模拟 m 2 = Π ( f ∗ ) m_2=\Pi(f^*) m2=Π(f∗)作为响应。
●对于 K K K定义中使用的 K A . k e y 1 ( a , Π ( P ( H 1 ( x ) ) ) ) KA.key_1(a,\Pi(P(H_1(x)))) KA.key1(a,Π(P(H1(x))))形式的每个表达式:
–如果 P ( H 1 ( x ) ) = f ∗ P(H_1(x))=f^* P(H1(x))=f∗,则用 k k k替换整个表达式(输入此简化算法)。
–否则,用将整个表达式替换为 K ( Π ( P ( H 1 ( x ) ) ) ) K(\Pi(P(H_1(x)))) K(Π(P(H1(x))))的结果,其中 K K K是简化算法的预言。由于 Π \Pi Π是一个排列,我们有 Π ( P ( H 1 ( x ) ) ) ≠ Π ( f ∗ ) = m 2 \Pi(P(H_1(x)))\neq \Pi(f^*)=m_2 Π(P(H1(x)))=Π(f∗)=m2;换句话说,在 m 2 m_2 m2上从不调用预言 K K K。
直观地说,这个简化算法在不知道KA随机值 a a a的情况下运行混合交互。相反, a a a通过 m 1 m_1 m1、 k k k和预言 K K K的隐式使用。
当输入𝑘是正确的键𝑘=KA.key1(𝑎,𝑚2),那么模拟完全匹配Hybrid(2,𝑖−1),因为减少正确地使用𝑘代替表达式KA。key1(𝑎,Π(𝑓∗))=KA.key1(𝑎,𝑚2)。
当输入 k k k是正确的密钥 k = K A . k e y 1 ( a , m 2 ) k=KA.key_1(a,m_2) k=KA.key1(a,m2),那么模拟完全匹配混合 ( 2 , i − 1 ) (2,i-1) (2,i−1),因为归约正确地使用 k k k代替表达式 K A . k e y 1 ( a , Π ( f ∗ ) ) = K A . k e y 1 ( a , m 2 ) KA.key_1(a,\Pi(f^*))=KA.key_1(a,m_2) KA.key1(a,Π(f∗))=KA.key1(a,m2)。
现在考虑一下𝑘是一个随机密钥。然后,每当 P ( H 1 ( x ) ) = f ∗ P(H_1(x))=f^* P(H1(x))=f∗时,将值 H 2 ( x , k ) H_2(x,k) H2(x,k)添加到 K K K中。因为 H 2 H_2 H2是一个随机的预言,并且因为 k k k是统一的(并且 ∣ k ∣ ≥ k \mid k\mid \ge k ∣k∣≥k),输出 H 2 ( x , k ) H_2(x,k) H2(x,k)与随机无法区分,即使对于多个 x x x值(例如,在对手构造 P P P的情况下,使对于多个 x x x值,有 P ( H 1 ( x ) ) = f ∗ P(H_1(x))=f^* P(H1(x))=f∗)。综上所述,当 k k k是均匀的时,模拟与混合 ( 2 , i ) (2,i) (2,i)没有区别,在这些情况下,在集合 K K K中添加一个随机值。KA的不可塑性意味着这两种情况无法区分。
优化。当KA是一轮密钥协定协议时(即,消息2不依赖于消息1,如在Diffie-Hellman实例中),那么可以将来自发送者的两个消息 m m m和 K K K合并。这就导致了一个2轮的PSI协议,其中第一个流是来自接收方的 P P P,而第二个流是来自发送方的 m m m, K K K。
请注意,最后一条消息的方向(从发送方到接收方的 H 2 H_2 H2输出)很重要。通过让接收方向发送方发送 H 2 H_2 H2输出,不可能保存一轮通信。这些 H 2 H_2 H2输出是使用一个公共 a a a(由发送方选择)和各种 b i b_i bi(由接收方选择)之间的KA结果来计算的。知道 a a a,发送方可以计算对任何 x x x“正确的” H 2 H_2 H2,因此接收方将通过发送他们的 H 2 H_2 H2输出集来暴露字典攻击。
如果只需要针对半诚实的对手进行安全保护,那么协议可以稍微简化,如下所示(详细信息见附录A):
●多项式可以在值 P ( y i ) P(y_i) P(yi)上被插值而不是 P ( H 1 ( y i ) ) P(H_1(y_i)) P(H1(yi)); H 1 H_1 H1仅用于帮助提取。
●发送者可以简单地发送 k i k_i ki的值,而不是发送形式如 H 2 ( x i , y i ) H_2(x_i,y_i) H2(xi,yi)的值。同样, H 2 H_2 H2仅用于提取。此外, k i k_i ki值的长度只能为 λ + 2 log ( n ) \lambda +2\log{(n)} λ+2log(n),以确保概率为 1 − 2 − λ 1-2^{-\lambda} 1−2−λ的正确性。
在附录B中还给出了另外两种可能的优化方法。
成本。发送方必须计算一个KA消息和 n n n个KA密钥/输出。接收方计算 n n n个KA响应和 n n n个KA密钥/输出。双方都对 H 1 H_1 H1、 H 2 H_2 H2和 Π ± \Pi^{\pm} Π±分别进行 n n n次查询。最后,接收方必须插值一个 n n n次的多项式,发送方必须在 n n n点上计算这样一个多项式。这些都可以通过 O ( n log 2 n ) O(n\log^2{n}) O(nlog2n)字段操作实现,如第2.3节所述。
该协议的总通信成本包括:(1)来自发送方的1个KA消息,(2)来自接收器的 n n n个域元素(每个大小相当于KA响应)来描述 P P P,(3) H 2 H_2 H2的 n n n个输出,每个 2 k 2k 2k位。
4.1 敌手集合的大小
回想一下,我们认为是一个理想的功能,腐败的一方可以提供一个“比敌手更大”的输入集合。如果一个腐败方(具体来说,接收方)提供了一个尽可能大的输入,那么PSI就不提供任何安全性。因此,绑定模拟器提取的集合的大小是很重要的。
腐败的发送方。发送方在协议期间给出一个集合 K K K,它应该包含 H 2 − H_2- H2−输出。对于一个适当的值 k k k,模拟器通过寻找 x x x来提取 H 2 ( x , k ) ∈ K H_2(x,k)\in K H2(x,k)∈K。由于 H 2 H_2 H2的输出是 2 k 2k 2k位,所以对手在 H 2 H_2 H2中遇到碰撞的概率可以忽略不计。因此,对于 K K K中的每个项目,对手/模拟器中最多有一个已知的预图像,因此最多有一个项目将包含在提取的集合 X ~ \tilde{X} X~中。
换句话说,模拟器最多为 ∣ K ∣ = n \mid K\mid =n ∣K∣=n个腐败的发送方提取输入集。该协议严格地强制执行一个腐败的发送方的输入集的大小。
腐败的接收方。模拟器为一个腐败的接收方提取的输入集合为: Y ~ = { y ∣ y ∈ O 1 a n d P ( H 1 ( y ) ) ∈ O Π } \tilde{Y}=\{y\mid y\in O_1\quad and \quad P(H_1(y))\in O_{\Pi}\} Y~={y∣y∈O1andP(H1(y))∈OΠ}。
抽象地说,敌手看到 H 1 H_1 H1的 q q q个输出,也看到 Π \Pi Π的 q q q个输出。在仿真中, H 1 H_1 H1和 Π \Pi Π的输出都是均匀的。然后敌手生成一个阶数小于 n n n(大于0)的多项式 P P P,然后模拟器检查对于所有 H 1 H_1 H1的输出 α \alpha α和所有 Π \Pi Π的输出 β \beta β是否有 P ( α ) = β P(\alpha)=\beta P(α)=β。这类对的数量是被提取的集合的大小。因此,问题是在阶数小于 n n n的多项式上敌手可以匹配多少个随机点?
CDJ表明,如果域的大小为 2 n ω ( log k ) 2^{n\omega (\log {k})} 2nω(logk),那么以压倒性的概率,没有一个多项式可以匹配比它的阶所表示的更多的点。然而,如此大的域会导致二次总通信(超过 2 n 2n 2n个元素的域中的 n n n系数)。相反,我们更喜欢坚持使用大小最小的域(仅大到足以编码一个KA消息),并获得项目数量的边界。
定义 4.4.设 F F F是一个域并定义对抗敌手 A A A的 P o l y O v e r f i t F n , n ′ ( q ) PolyOverfit_{F}^{n,{n}'}(q) PolyOverfitFn,n′(q)如下所示:
换句话说,敌手试图生成一个多项式,在至少 n ′ {n}' n′不同的 α i \alpha _i αi上击中一些 β j \beta_j βj。
我们说 P o l y O v e r f i r F n , n ′ PolyOverfir_{F}^{n,{n}'} PolyOverfirFn,n′是困难的,如果对于所有的多项式 q q q和所有的 P P T A PPT A PPTA,对手以可以忽略不计的概率获胜。
结论 4.5.如果 P o l y O v e r f i t F n , n ′ PolyOverfit_{F}^{n,{n}'} PolyOverfitFn,n′是困难的,那么在我们的PSI协议中,一个腐败的接收器的模拟器输出一组以 n ′ {n}' n′为界的大小,除了可以忽略不计的概率。
在附录C中,我们使用一个标准的压缩参数来显示以下内容。如果存在这样种“过拟合”多项式,它可以被用于生成 α i \alpha_i αi和 β i \beta_i βi的压缩表示,如果它们是一致的,但这是不可能的。
引理4.6. 赢过 P o l y O v e r f i t F n , n ′ PolyOverfit_{F}^{n,{n}'} PolyOverfitFn,n′的概率至多为 ( q 2 n ) n ′ / ∣ F ∣ n ′ − n {(q^2n)}^{{n}'}/{\mid F \mid }^{{n}'-n} (q2n)n′/∣F∣n′−n。
下面给出了一些以 ∣ F ∣ = 2 256 \mid F \mid =2^{256} ∣F∣=2256为界限的具体的例子:
例如,当为 n = 2 10 n=2^{10} n=210个项目运行协议时,敌手将有很高的可能性无法获得大小为 8 n + 4 8n+4 8n+4的有效输入。
我们强调上面的界是无条件的,这意味着对于上面的参数,这样的“过拟合”多项式根本不存在,除非有可以忽略的概率。似乎有理由合理地推测,即使这样的多项式存在,对于 P P T PPT PPT的敌手来说也是很难找到它们的。如果这样的主张被证实,这将意味着在我们的协议中更严格的执行集合大小。
我们还强调,所有基于OT扩展的恶意PSI协议在腐败各方集的大小上都有类似的“松弛”。在[46]中陈述了 n ′ = 6 n {n}'=6n n′=6n的界;在[47]中陈述了 n ′ = 4 n {n}'=4n n′=4n的界;在[43]中,给出了不同参数下 c ∈ { 2 , 3 , 4 , 5 } c\in \{2,3,4,5\} c∈{2,3,4,5}的界 n ′ = 2.4 c n {n}'=2.4cn n′=2.4cn的范围。
5 实验结果
5.1 实施
为了评估我们的PSI协议的性能,我们构建并评估了一个实现。我们的完整实现可以在GitHub:https://github.com/osu-crypto/MiniPSI上获得。下面,我们将讨论我们是如何实例化各种组件的。
关键协议。我们使用椭圆曲线组实例化DHKA,并使用SHA2求 g a b g^{ab} gab的哈希值。如前所述,在ODH假设下,DHKA的这种变体是不可塑的(定义3.3)。
椭圆曲线由域 F q F_q Fq上的Weierstrass方程 y 2 = x 3 + A x 2 + B y^2=x^3+Ax^2+B y2=x3+Ax2+B或Montgomery方程 y 2 = x 3 + A x 2 + x y^2=x^3+Ax^2+x y2=x3+Ax2+x的解 ( x , y ) (x,y) (x,y)组成。根据曲线参数的不同,EC在平面上显示不同的形状。在这项工作中,我们选择了Curve25519 Montgomery曲线,因为它被推荐为elligator[1]。这个Curve25519被定义在 G F ( q = 2 255 − 19 ) GF(q=2^{255}-19) GF(q=2255−19)上,且其曲线参数 A A A的值为486662。
我们实现了基于[6]的椭圆曲线编码。该编码取一个曲线点,并输出一个256位的伪随机串。如果该点 ( x , y ) (x,y) (x,y)满足两个条件,则它有一个逆映射: x x x值不等于曲线参数𝐴;且 − 2 x ( x + a ) -2x(x+a) −2x(x+a)必须是一个正方形。因此,我们一直保持采样点,直到这些条件保持不变。根据[1,6]和我们的实验证实,成功的概率为 1 / 2 1/2 1/2。该有效点的椭圆曲线编码由 r = ( − 1 2 ) ( x x + A ) b r=\sqrt{(\frac{-1}{2}){(\frac{x}{x+A})}^b} r=(2−1)(x+Ax)b定义,其中,如果 v ≤ q − 1 2 v\le \frac{q-1}{2} v≤2q−1则 b = 1 b=1 b=1,否则为𝑏=−1。解密函数取一个字符串 r r r,并产生Curve25519上的一个点的 x x x坐标。值 x x x可以被计算为 x = e d − ( 1 − e ) A 2 x=ed-(1-e)\frac{A}{2} x=ed−(1−e)2A,其中 d = − A 1 + 2 r 2 d=\frac{-A}{1+2r^2} d=1+2r2−A而 e = ( d 3 + A d 2 + d ) q − 1 2 e={(d^3+Ad^2+d)}^{\frac{q-1}{2}} e=(d3+Ad2+d)2q−1。我们在由libsodium库实现的Curve25519的顶部实现elligator。从我们的实现评估来看,libsodium库比miracl库的速度快10倍。
椭圆曲线编码的长度略小于256位。为了促进这些编码在 { 0 , 1 } 256 {\{0,1\}}^{256} {0,1}256中是均匀的,我们可以附加一些额外的均匀位,它们在解密过程中被忽略。这些额外的位可以被认为是KA协议中的随机性的一部分,它们导致协议消息在 F = { 0 , 1 } 256 F={\{0,1\}}^{256} F={0,1}256中是伪随机的。
其他原语。我们使用SHA2实例化必要的随机预言。由于椭圆曲线有256位编码,我们需要一个定义在 { 0 , 1 } 256 {\{0,1\}}^{256} {0,1}256以上的理想排列 Π ± {\Pi}^{\pm} Π±。在我们的实现中,我们使用带有固定密钥的Rijndal-256作为理想的排列。
多项式运算。我们的协议要求接收方生成一个 n n n阶的多项式,而发送方在 n n n个点上计算它。这些问题可以通过拉格朗日插值和霍纳计算来解决,这需要 O ( n 2 ) O(n^2) O(n2)域运算。然而,当 n n n非常大时(例如 n = 2 20 n=2^{20} n=220),这就变得不现实了。Moenck和Borodin描述了在 O ( n log 2 n ) O(n\log^2{n}) O(nlog2n)域运算中解决这些问题的算法,这使它们更适合我们的协议。
安全参数。所有的评估都是使用PSI项目长度为128位、计算安全参数 κ = 128 \kappa=128 κ=128位和统计安全参数 λ = 40 \lambda=40 λ=40位进行的。
5.2 实验和评估
实验设置。我们在C++中实现了我们的协议,并在一个具有2.30 GHz和256GB内存的Intel Xeon上运行我们的协议。双方通过一个模拟的10Gbps网络进行通信,以0.2 ms的往返时间进行局域网设置。我们还在广域网设置中运行所有协议,使用80 ms的往返时间,两种不同的网络带宽为50Mbps和1Mbps。
协议评估。下面,我们对最先进的半诚实和恶意PSI协议[11,16,29,36,42,43]进行基准测试。我们现在简要讨论几种比较中不包括的协议:Jarecki-Liu的协议[34]是恶意安全且基于DH的。然而,它实现了一个较弱的理想功能,即敌手可以自适应地选择项目。Rindal&Schoppmann的PSI协议是基于silent vector-OLE,并且对大集合的效率非常高。然而,它的实现还没有公开,而且它的高固定成本使得它对小集合的效率低下(如表1所示)。Chen等人的工作[12]是最先进的(片面的)基于FHE的恶意PSI。它的第一步基本上是经典的DH-PSI,甚至在做任何FHE操作之前。由于我们的整个协议比DH-PSI更有效,我们预计我们的协议将比他们的中小型协议集快得多。
我们也不包括基于RSA的PSI协议[3,17],即我们指的是每个项目至少需要一个RSA指数化的协议。RSA元素比椭圆曲线(ECC)元素大16(=4096/256)倍。在我们的实验硬件(openssl speed rsa4096 ecdh×25519)上的一个简单的基准测试表明RSA-4096的指数比ECC指数要慢100倍(即使RSA-2018也要慢20倍)。因此,基于RSA的协议将总是比我们的协议慢约100倍。如果他们每个项目发送一个RSA值,他们将比我们多16倍的通信。
我们在表2和表3中报告了小集合 { 2 7 , 2 8 , 2 9 , 2 10 } \{2^7,2^8,2^9,2^{10}\} {27,28,29,210}和大集合 n ∈ { 2 12 , 2 16 , 2 20 } n\in \{2^{12},2^{16},2^{20}\} n∈{212,216,220}的详细比较。正如预期的那样,当集合很小时,我们的协议显示出了显著的性能改进。
我们注意到,我们的poly-DH PSI协议非常适合预先计算(通过预先计算指数)。
在报告这些协议的性能时,我们将总运行时间分为两个阶段:
●离线:像生成随机对 ( r i , g r i ) (r_i,g^{r_i}) (ri,gri)这样的操作,可以在没有任何交互的情况下在输入之前完成。
●在线:其他的一切,从双方决定了他们的输入后就开始了。
宽带比较。我们的基于多项式的协议是所有PSI协议之间通信最低的。我们的基于多项式的协议的通信大约比经典的DH PSI小2倍。与恶意的DH基PSI协议(DKT)相比,我们的协议大约有3~4倍的改进。
考虑一个具有不相等集合大小的半诚实PSI,基于多项式的PSI协议的通信成本为 ( n 1 ∣ G ∣ + n 2 l ) (n_1\mid G \mid +n_2l) (n1∣G∣+n2l)位,而基于DH的经典PSI的通信成本约为 ( ( n 1 + n 2 ) ∣ G ∣ + n 2 l ) ((n_1+n_2)\mid G \mid +n_2l) ((n1+n2)∣G∣+n2l)位。具体地说,对于 n 1 = 2 16 n_1=2^{16} n1=216和 n 2 = 2 20 n_2=2^{20} n2=220,基于多项式的协议需要12.58MB的通信,而经典的DH PSI需要46.14MB,改进了3.67倍。
我们还与最先进的基于[11,36,42]的半诚实PSI协议[11,36,42]和恶意PSI协议[43]进行了带宽比较。请注意,36和43是迄今为止最快的PSI协议,而11在中等带宽(如30-100Mbps)的网络中通信速度最快,而42在实际的半诚实协议中通信最少。我们的协议的通信成本分别比[36]、[42]和[43]低约3~4.6倍、1.4 ~ 1.7倍和3.7 ~7.8倍
运行时间比较。对于小集(例如 n = 2 9 n=2^9 n=29),我们在局域网和广域网设置中,基于多项式的协议比所有基于DH和基于OT的方案都要快。从 n = 2 1 0 n=2^10 n=210开始,在局域网设置中,我们的协议比基于OT的协议要慢。然而,在WAN设置中使用1Mbps网络带宽和80 ms往返延迟对所有协议进行基准测试,由于通信成本最小,我们的协议比其他协议快1−3.17倍。
基于多项式的协议显示了它在不平衡设置中的好处,即发送方的集合大小大于接收方的集合大小 ( n 2 > n 1 ) (n_2 > n_1) (n2>n1)。这意味着发送方只需要为接收方的集合中的每个项目发送一个短的指纹 ℓ \ell ℓ,而在基于DH的协议中,发送方额外需要为每个项目发送一个组元素。由于PaXoS和DKT的实现不支持计算非对称集的PSI,因此我们省略了报告它们的性能成本。表3显示,在大多数情况下,我们的基于多项式的协议的运行时间比其他半诚实的协议更快。因此,我们的协议比其他恶意协议更快。对于带宽为1Mpbs的广域网设置中的 n 1 = 2 16 n_1=2^{16} n1=216和 n 2 = 2 20 n_2=2^{20} n2=220,基于DH协议运行时间为574.26秒,而基于多项式的协议需要117.81秒,分别是4.9倍和3.1倍的改进。
图1展示了最新技术(包括本工作)的总结,其中运行时间是在LAN设置中测量的。由于其非常低的通信复杂度,我们的PSI协议协议的性能几乎不受改变网络带宽和延迟的影响。
结论。对于小集 ( n ≤ 512 ) (n \le 512) (n≤512),我们的协议在通信和计算方面都是最好的。正如我们之前在第1节中讨论的,在这种大小的集上,我们的协议比基于OTs(需要OT扩展)的PSI协议更便宜。













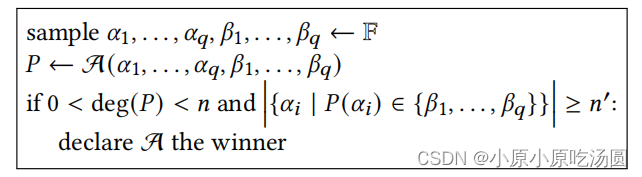















 751
751











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








