长方形有多少条线段_小学奥数 数线段 图形 三角形 长方形入门

一、学会数图形

要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数，从中发现规律，以便得到正确的结果。

要正确数出图形的个数，关键是要从基本图形入手。首先要弄清图形中包含的基本图形是什么，有多少个，然后再数出由基本图形组成的新的图形，并求出它们的和。

当我们识了线段、角、三角形、长方形等基本图形后，这些图形重重叠叠地交错在一起时就构成了复杂的几何图形。要想准确地计数这类图形中所包含的某一种基本图形的个数，就需要仔细地观察，灵活地运用有关的知识和思考方法，掌握数图形的规律，才能获得正确的结果。

 二、解题策略

要准确、迅速地计数图形必须注意以下几点：

1.弄清被数图形的特征和变化规律。

2.要按一定的顺序数，做到不重复，不遗漏。

 考点一：基本图形

例1、数出下图中有多少条线段？

【解析】方法一：我们可以采用以线段左端点分类数的方法。以A点为左端点的线段有：AB、AC、AD 3条；以B点为左端点的线段有：BC、BD 2条；以C点为左端点的线段有：CD 1条。所以，图中共有线段3+2+1=6(条)。

方法二：把图中线段 AB、BC、CD看做基本线段来数，那么，由1条基本线段构成的线段有：AB、BC、CD 3条；由2条基本线段构成的线段有:AC、BD 2条；由3条基本线段构成的线段有：AD 1条。所以，图中一共有3+2+1=6(条)线段。

 例2、数出图中有几个角？

【解析】数角的个数可以采用与数线段相同的方法来数。

方法一：以OA为一边的角有：∠AOB、∠AOC、∠AOD 3个；以OB为一边的角还有：

∠BOC、∠BOD 2个；以OC为一边的角还有：∠COD 1个。所以，图中共有角3+2+1=6(个)。

方法二：把图中∠AOB、∠BOC、∠COD看做基本角来数，那么，由1个基本角构成的角有：∠AOB、∠BOC、∠COD 3个；由2个基本角构成的角有: ∠AOC、∠BOD 2个；由3个基本角构成的角有：∠AOD 1个。所以，图中一共有3+2+1=6(个)角。

例3、数出右图中共有多少个三角形？

【解析】方法一：我们可以采用按边分类数的方法。以PA为边的三角形有：△PAB、△PAC、△PAD、3个；以PB为边的三角形还有：△PBC、△PBD 2个；以PC为边的三角形还有：△PCD 1个。所以，图中共有三角形3+2+1=6(个)。方法二：把图中三角形 △PAB、△PBC、△PCD看做基本三角形来数，那么，由1个基本三角形构成的三角形有：△PAB、△PBC、△PCD 3个；由2个基本三角形构成的三角形有: △PAC、△PBD 2个；由3个基本三角形构成的三角形有：△PAD 1个。所以，图中一共有3+2+1=6(个)三角形。方法三：我们发现，要数出图中三角形的个数，只需数出线段 AD中包含几条线段就可以了，即3+2+1=6(个)。所以图中共有6个三角形。

 考点二：较复杂的问题

例1、数出下图中有多少个长方形？

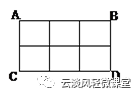
【解析】数图中有多少个长方形和数三角形的方法一样，长方形是由长、宽两对线段围成，线段 CD上有3+2+1=6(条)线段，其中每一条与AC中一条线段对应，分别作为长方形的长和宽，这里共有6×1=6(个)长方形，而AC上共有2+1=3(条)线段也就有6×3=18(个)长方形。它的计算公式为：

长方形的总数=长边线段的总数×宽边线段的总数：

(3+2+1)×(2+1)=18(个) 

例2、有5个同学，每两个人握手一次，一共要握手多少次？

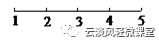
【解析】这道题可以用数线段的方法来解答。根据题意，画出线段图，每一个端点代表一个同学。

从图上可以看出，第1个同学要与其余4个同学握手共握手4次；第2个同学还要与其余3个同学握手共握手3次，第3个同学要与其余2个同学握手共握手2次；第4个同学还要与最后1个同学握手共握手1次。所以，一共要握手4+3+2+1=10(次)

 例3、从广州到北京的某次快车中途要停靠8个大站，铁路局要为这次快车准备多少种不同车的车票？这些车票中有多少种不同的票价？

【解析】这道题是数线段的方法在实际生活中的应用，连同广州、北京在内，这条铁路上共有10个站，共有1+2+3+…+9=45条线段，因此要准备45种不同的车票。由于这些车站之间的距离各不相等，因此，有多少种不同的车票，就有多少种不同的票价，所以共有45种不同的票价。