计算机视觉--SIFT特征提取与检索

1、SIFT算法简介

1.1 算法概述

SIFT全称尺度不变特征转换。它用来侦测与描述影像中的局部性特征，它在空间尺度中寻找极值点，并提取出其位置、尺度、旋转不变量。SIFT算法的实质可以归为在不同 尺度空间 上查找 特征点（关键点） 的问题。

1.2 相关概念

1.2.1 关键点

关键点是指一些十分突出的点，这些点不会因光照、尺度、旋转等因素的改变而消失，比如角点、边缘点、暗区域的亮点以及亮区域的暗点。

1.2.2 尺度空间

概念：
尺度空间理论最早于1962年提出，其主要思想是通过对原始图像进行尺度变换，获得图像多尺度下的空间表示。从而实现边缘、角点检测和不同分辨率上的特征提取，以满足特征点的尺度不变性。
表示：
SIFT算法在构建尺度空间时采取高斯核函数进行滤波，使原始图像保存最多的细节特征，经过高斯滤波后细节特征逐渐减少来模拟大尺度情况下的特征表示。利用高斯核函数进行滤波的主要原因有两个：
（1）高斯核函数是唯一的尺度不变核函数。
（2）DoG核函数可以近似为LoG函数，这样可以使特征提取更简单。

一个图像的尺度空间L(x, y, σ) ，定义为原始图像 I(x, y)与一个可变尺度的2维高斯函数G(x, y, σ) 卷积运算。公式如下：

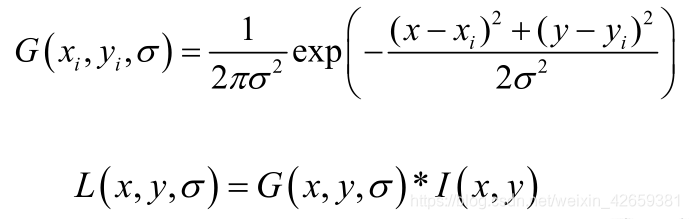
其中*表示卷积运算，(x,y)代表图像的像素位置。是尺度空间因子，值越小表示图像被平滑的越少，相应的尺度也就越小。大尺度对应于图像的概貌特征，小尺度对应于图像的细节特征。

1.2.3 高斯金字塔

构建：
尺度空间在实现时使用高斯金字塔表示，高斯金字塔的构建分为两步：
（1）对图像做高斯平滑。
（2）对图像做降采样。

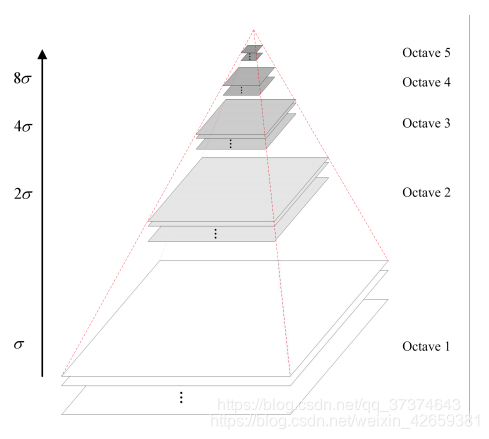
为了让尺度体现其连续性，高斯金字塔在简单降采样的基础上加上了高斯滤波。如上图所示，将图像金字塔每层的一张图像使用不同参数做高斯模糊，Octave表示一幅图像可产生的图像组数，Interval表示一组图像包括的图像层数。
表示：
高斯图像金字塔共o组、s层，则有：

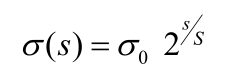
σ：尺度空间坐标；s：sub-level层坐标；σ0：初始尺度；S：每组层数（一般为3~5）
最后可将组内和组间尺度归为：

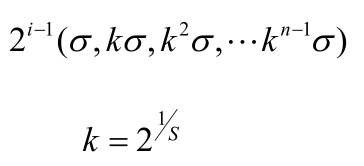
i：金字塔组数；n：每一组的层数

1.2.4 DOG空间极值检测

DOG函数：

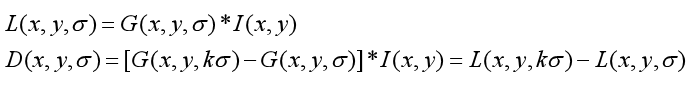
DOG高斯差分金字塔：
（1）对应DOG算子，需构建DOG金字塔。

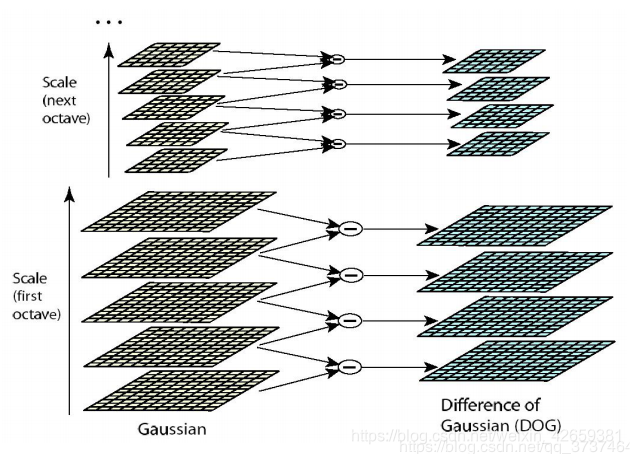
可以通过高斯差分图像看出图像上的像素值变化情况。（如果没有变化，也就没有特征。特征必须是变化尽可能多的点。）DOG图像描绘的是目标的轮廓。
（2）DOG局部极值检测
特征点是由DOG空间的局部极值点组成的。为了寻找DoG函数的极值点，每一个像素点要和它所有的相邻点比较，看其是否比它的图像域和尺度域的相邻点大或者小。

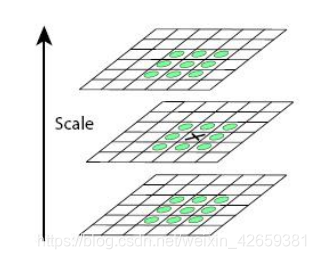
中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个
点共26个点比较，以确保在尺度空间和二维图像空间都检测到极值点。
去除边缘响应：
由于DoG函数在图像边缘有较强的边缘响应，因此需要排除边缘响应。DoG函数的峰值点在边缘方向有较大的主曲率，而在垂直边缘的方向有较小的主曲率。主曲率可以通过计算在该点位置尺度的2×2的Hessian矩阵得到，导数由采样点相邻差来估计：

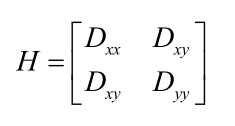
Dxx 表示DOG金字塔中某一尺度的图像x方向求导两次。
D的主曲率和H的特征值成正比。令 α ，β为特征值，则

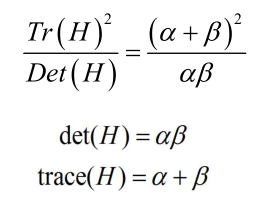
该值在两特征值相等时达最小。Lowe论文中建议阈值T为1.2，即
时保留，反之剔除。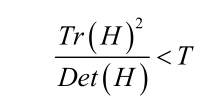

1.2.5 关键点方向匹配

通过尺度不变性求极值点，可以使其具有缩放不变的性质。而利用关键点邻域像素的梯度方向分布特性，可以为每个关键点指定方向参数方向，从而使描述子对图像旋转具有不变性。通过求每个极值点的梯度来为极值点赋予方向。像素点的梯度表示：

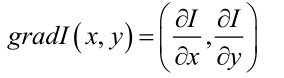
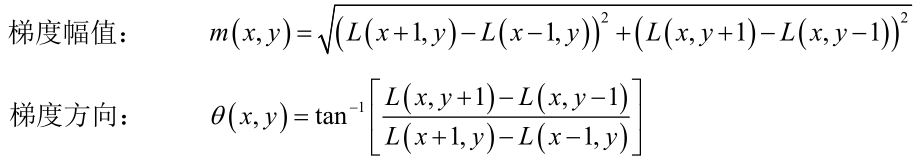
1.2.6 关键点描述

对于每一个关键点，都拥有位置、尺度以及方向三个信息。为每个关键点建立一个描述符，用一组向量将这个关键点描述出来，使其不随各种变化而改变，比如光照变化、视角变化等等。这个描述子不但包括关键点，也包含关键点周围对其有贡献的像素点，并且描述符应该有较高的独特性，以便于提高特征点正确匹配的概率。

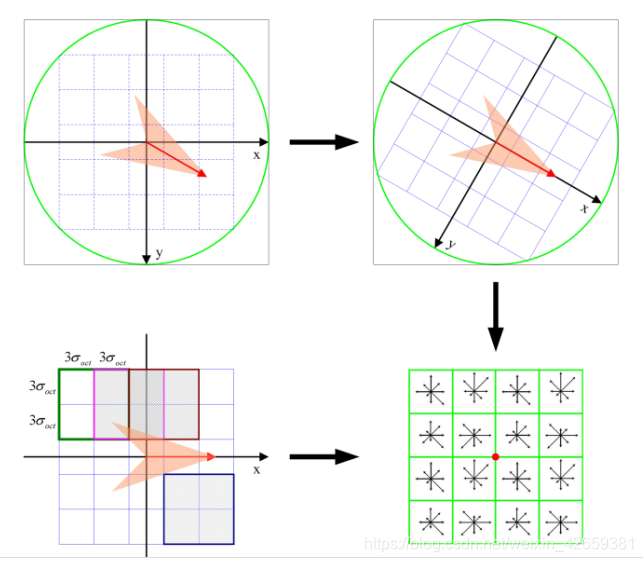
Lowe实验结果表明：描述子采用4×4×8＝128维向量表征，综合效果最优（不变性与独特性）。

1.2.7 关键点匹配

关键点的匹配可以采用穷举法来完成，但是这样耗费的时间太多，一
般都采用kd树的数据结构来完成搜索。搜索的内容是以目标图像的关
键点为基准，搜索与目标图像的特征点最邻近的原图像特征点和次邻
近的原图像特征点。Kd树是一个平衡二叉树，如下所示：

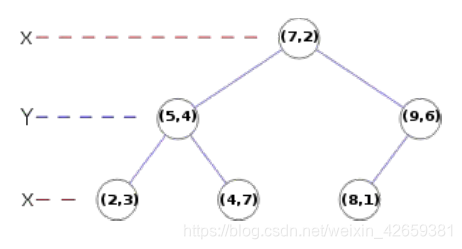
2、图像特征提取，并展示特征点

2.1 数据集

2.2 数据集特征提取结果展示

SIFT算法与Harris算法的比较

2.3 小结

• 以上实验拍摄了室内外不同场景，以及同一场景的不同角度不同尺度的图片。
• 从以上实验结果来，如对同一幅画不同角度不同尺度的拍摄，SIFT算法检测出来的特征点并无太大的区别，画中的特征点和墙上的细小特征点都没有基本一致，证明SIFT算法具有旋转不变性、尺度不变性、亮度不变性，以及SIFT算法的对于局部特征的提取是非常的稳定的。
• SIFT算法与Harris算法的比较：SIFT算法检测出来的特征点多于Harris角点检测出来的角点，体现出SIFT算法通过多次的采样，卷积等操作，输出的结果较为精准。且从运行的时间上相比，SIFT算法比Harris算法效率高。Harris角点只是对原图进行角点检测和变化，Harris特征点检测存在角点信息丢失与偏移的现象。

2.4 源代码

# -*- coding: utf-8 -*-
from PIL import Image
from pylab import *
from PCV.localdescriptors import sift
from PCV.localdescriptors import harris

# 添加中文字体支持
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"c:\windows\fonts\SimSun.ttc", size=14)

imname = 'C:/TXX/1.png'
im = array(Image.open(imname).convert('L'))
sift.process_image(imname, 'empire.sift')
l1, d1 = sift.read_featur