数据结构与算法-浙江大学陈越数据结构第一章学习

一.什么是数据结构

关于什么是数据结构,官方没有统一的定义,陈越老师对于这个问题列举了3个(sartaj sahni,Clifford A.Shaffer,中文维基百科)描述，从中我们发现数据结构和算法息息相关。

然后陈越老师列举了以下3个例子,来理解数据结构。
例1:如何在书架上摆放图书?
摆放图书的操作:

• 新书怎么插入
• 怎么找到某本指定图书

摆放图书的方法:

• 随便摆放(插入方便,当插入的图书数量较多时查找麻烦)
• 按照书名的拼音字母顺序排放(插入比较方便,查找比较方便)
• 把书架划分成几块区域，每块区域指定摆放某种类别的图书;在每种类别内，按照书名的拼音字母顺序排放(插入方便,查找方便,需要考虑类别划分,和空间分配问题)

从上面的例子我们可知:

• 解决问题方法的效率,跟数据的组织方式有关

例2:写程序实现一个函数PrintN，使得传入一个正整数为N的参数后，能顺序打印从1到N的全部正整数。
通过循环实现:

运行效果:

通过递归实现:

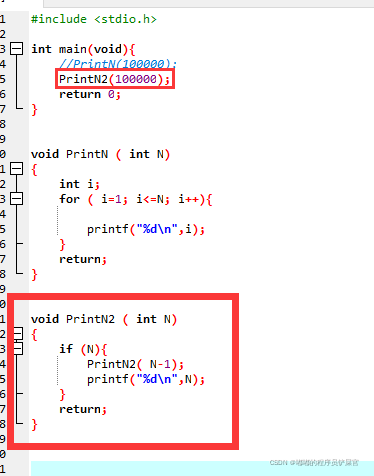
运行效果:

每一个程序,存放临时数据存储空间是有限的(使用的临时数据存放到内存中),上面的程序,每迭代一次,就会多一个临时数据，就会占用一个临时空间,当占的存储空间超过程序使用的存储空间的时候，就会非正常退出，出现像上面那样,没有任何结果输出。

从上面的例子可知:

• 解决问题方法的效率,跟空间的利用效率有关

c语言计时函数:

第一种求多项式方法: 通过f(x)=an X xⁿ 对每项求和

第二种求多项式方法: 秦九韶算法

具体代码:

#include <stdio.h>
#include <time.h>
#include <math.h>

clock_t start, stop; 
double duration;
double f1( int n, double a[], double x, int count);
double f2( int n, double a[], double x, int count);



int main (){
	double a[100];
	int i=0,count=10000000;
	for (i=0;i<10;i++){
		a[i]=i;
	}
	start = clock();
	// 被测函数
	f1(9,a,6,count);
	stop = clock();
	duration = ((double)(stop-start))/CLK_TCK/count;
	printf("第一种方法打点个数:%f\n",(double)(stop-start));
	printf("第一种方法运行时间:%6.2e\n",duration);
	
	start = clock();
	// 被测函数
	f2(9,a,6,count);
	stop = clock();
	duration = ((double)(stop-start))/CLK_TCK/count;
	printf("第二种方法打点个数:%f\n",(double)(stop-start));
	printf("第二种方法运行时间:%6.2e\n",duration);
	return 0; 
}

double f1( int n, double a[], double x,int count)
{
	int i;
	double p = a[0];
	while(count!=0){
		--count;
		for ( i=1; i<=n; i++){
			p += (a[i] * pow(x,i));
		}	
	}
	
	return p;
}

double f2( int n, double a[], double x,int count)
{
	int i;
	double p = a[0];
	while(count!=0){
		--count;
			for ( i=n; i>0; i--){
				p += a[i-1] + x*p;
			}	
	}
	
	return p;
}

运行效果:

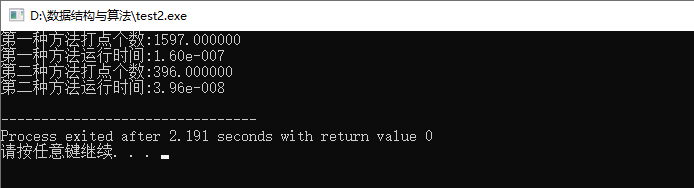
从上面的例子我们可知:

• 解决问题方法的效率,跟算法的巧妙程度有关

通过上面的实例,再来思考上面的问题(什么是数据结构)?

• 数据对象在计算机中的组织方式,分为逻辑结构(集合结构,线性结构,树形结构,图形结构)和物理结构(顺序存储和链式存储)
• 数据对象必定与一系列加在其上的操作相关联
• 完成这些操作所用的方法就是算法

备注:

• 逻辑结构:是指数据对象中数据元素之间的相互关系。
• 物理结构:是指数据的逻辑结构在计算机中的存储形式。

关于什么是抽象数据类型

• 数据类型:是指一组性质相同的值的集合及定义在此集合上的一些操作的总称(在面向对象语言中叫做类)。
• 抽象:是指抽取出事物具有的普遍性的本质。它是抽出问题的特征而忽略非本质的细节，是对具体事物的一个概括。抽象是一种思考问题的方式，它隐藏了繁杂的细节，只保留实现目标所必需的信息。
• 抽象数据类型(Abstract Data Type,ADT):是指一个数学模型及定义在该模型上的一组操作。抽象数据类型的定义仅取决于它的一组逻辑特性，而与其在计算机内部如何表示和实现无关(只描述数据对象集和相关操作集“是什么”，并不涉及“如何做到”的问题)。

二.什么是算法

1.定义

2.什么是好算法

衡量算法的好坏由时间复杂度和空间复杂度决定,并不仅仅只是时间复杂度或空间复杂度一方越好该算法就越好,而是根据实际场景,选择时间复杂度和空间复杂度的一个平衡点,有的时候为了追求运行速度我们会相应的舍弃一些空间来换取时间(提高运行速度),或者为了减少使用的空间降低运行的速度。

复杂度分析:

• T(N)= C·N

3.最坏情况复杂度与平均复杂度

• 最坏情况运行时间是一种保证，那就是运行时间将不会再坏了。在应用中，这是一种最重要的需求，通常，除非特别指定，我们提到的运行时间都是最坏情况的运行时间。
• 平均运行时间是所有情况中最有意义的，因为它是期望的运行时间。

4.复杂度的渐进表示法

(无需关心算法具体执行了多少次,只需要粗略地知道它的增长趋势即可)

• 上界
• 下界
• 等价

大O()记法:用来体现算法时间复杂度
推导大O阶

• 1.用常数1取代运行时间中的所有加法常数。
• 2.在修改后的运行次数函数中，只保留最高阶项。
• 3.如果最高阶项存在且不是1,则去除与这个项相乘的常数。

常数阶
以下代码的大O()表示为O(1)而不是O(3)=O(1+1+1)(由推导大O阶第1条可知)

同理以下代码的大O()表示为O(1)

事实上无论n为多少，上面的两段代码就是3次和12次执行的差异。这种与问
题的大小无关(n的多少)，执行时间恒定的算法，我们称之为具有0(1)的时间复杂
度，又叫常数阶。
注意:不管这个常数是多少，我们都记作0(1),而不能是0(3)、 0(12)等其他任何数字，这是初学者常常犯的错误。

线性阶
线性阶的循环结构会复杂很多。要确定某个算法的阶次，我们常常需要确定某个特定语句或某个语句集运行的次数。因此，我们要分析算法的复杂度，关键就是要分
析循环结构的运行情况。
下面这段代码，它的循环的时间复杂度为0(n)，因为循环体中的代码须要执行n次。

int i;
for(i=0;i<n;i++){
	/* 时间复杂度为O(1)的程序步骤序列
}

对数阶

平方阶

5.常见函数的输入规模

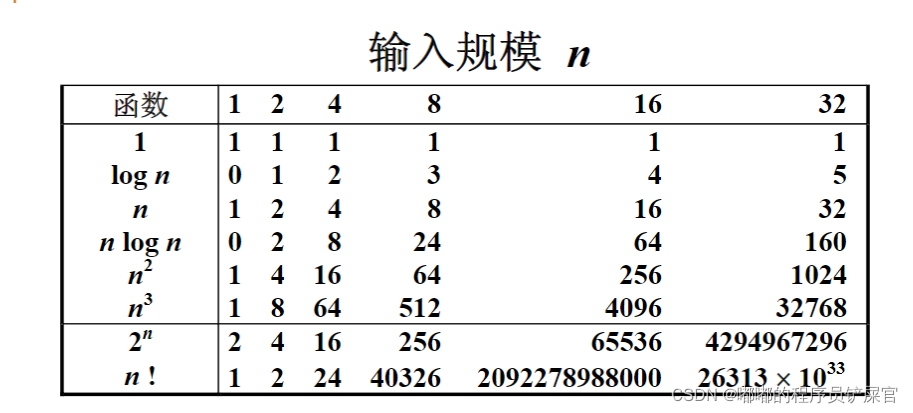
备注: 当我们编写的算法运行时间要大于nlogn的时候,我们尽量将该算法优化到nlogn。

6.复杂度分析小窍门

三.应用实例(最大子列和问题)

(1) 什么是最大子列和问题

(2) 算法1

(3) 算法2

(4) 算法3

4:4和-3二个数,不运算值为4,运算后值为1,所以最大为4
5:5和-2二个数,不运算值为5,运算后值为3,所以最大为5
6:4和-3(运算后1,不运算是4),4,-3和5(4和-3运算后为1再和5运算为6),4,-3,5,和-2(前面进行运算后为6如果再和-1运算就为5了,所以选择不运算为6),所以最大为6

(4) 算法4(在线处理)

四.常见数据结构

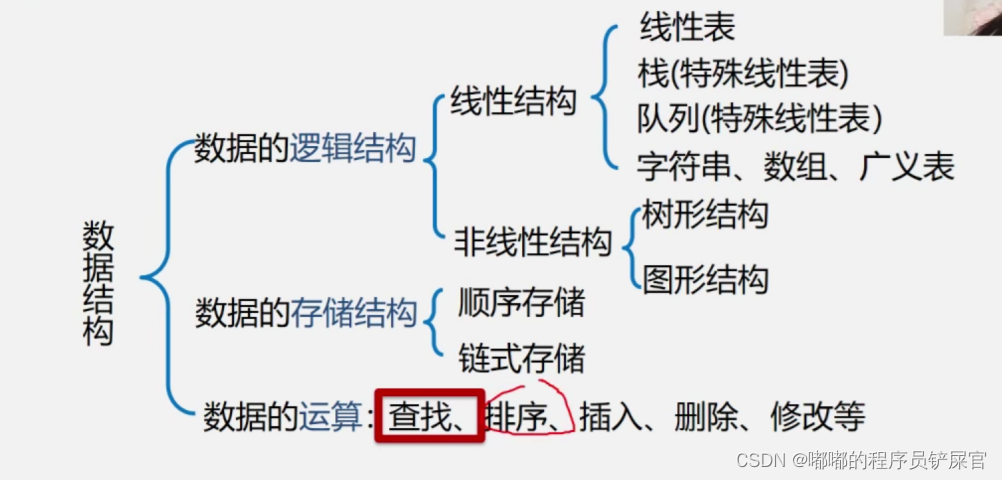
常用的数据结构可根据数据访问的特点分为线性结构和非线性结构。线性结构包括常见的链表、栈、队列等，非线性结构包括树、图等。

相关视频学习链接:
数据结构与算法基础（青岛大学-王卓）