【学习笔记】Hands on Machine Learning with Scikit-Learn, Keras, and Tensorflow - 第4章：训练模型

写在前面

本系列为本人自学Hands on Machine Learning with Scikit-Learn, Keras, and Tensorflow一书的个人学习笔记，目标有2个：

1. 帮助自己更好地理解机器学习的概念和主流模型方法

2. 设计尽可能最好理解的方法，中英结合，帮助更多人，哪怕是计算机和数学背景比较薄弱的朋友学习这本优质的机器学习英文书籍

写得比较随性，学到哪里就会同步最新进度，没写完的文档也会传上来供批评指正

GitHub代码链接：qinQiaoJUn/Hands_on_Machine_Learning_Study: Self-study of the book Hands on Machine Learning, with notes and codes

对应的代码实操笔记：【待更新】

版权所有，未经许可严禁搬运、抄袭、盗用或用作商业用途
 

1. 核心概念与关键思想

截止前3章结束，我们其实已经做了很多机器学习的实操了。但是，我们还不知道这些模型和训练算法内部是如何运行的

目前我们不管是对算法进行调优，还是根据任务选择模型，其实都是跟着Geron大神的节奏，他让我们怎么做，我们就怎么做

那我们要是自己开发项目，总不能让Geron大神一个个指导吧（而且他的想法也未必完美）

因此，第4章的重点会放在让我们自己理解如何训练模型、发现过程中的偏差、以及怎么调整这些“更独立”的操作上。有了这一章的知识，我们就能更加清楚模型里面到底发生了什么，我们如何形成自己的方法论来应对

注意：本章涉及的数学知识会增多，包括代数、微积分、线性代数。为了理解本章的数学公式，我们需要先了解向量和矩阵的概念，如何转置、相乘、以及求逆矩阵。

2. 重点模型和算法理解

2.1 线性模型引入

一般来说，一个线性模型遵循以下等式进行预测：

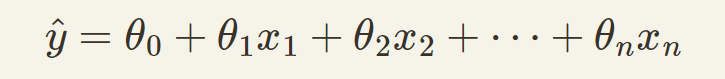
其中ŷ是预测值，n是特征值的总个数，xi是第i个特征值，θ是每个特征值对应的参数

这个模型也可以用向量的方式来表示：

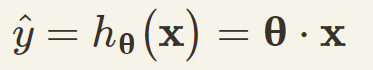
其中ŷ是预测值

hθ(x)是预测函数，用的是θ这个特征值向量

θ是模型的参数向量，包含偏置项θ0（bias term）和其余特征权重（θ1到θn）

x是每个实例的特征向量，包含x0到xn，其中x0一定是1（因为θ0x0这一项一定只有θ0这个偏置项）

------------------------------------------停一下------------------------------------------

行了，都写到这了，如果你是第一次接触这些东西，能看得懂吗？

因为我从小数理化不好，但又喜欢计算机，所以我希望用最能让大家理解的方式把这些概念讲清楚，而不是甩一堆数学公式就结束。看过了3Blue1Brown大神的视频后，我真的觉得数学的本质是很清楚、很具体的，并不是一堆抽象的表达。抽象成公式只是为了在理解的基础上，表达得更简洁

所以让我们把上面这一串忘了！用一个例子来说明：

2.2 举个生活化的例子：幸福指数

我们就用第一章的幸福指数来举例：

一个国家或地区的幸福指数，可能是由很多因素决定的，比如工资水平、人口密度、医疗条件、每周可自由支配的时间，等等

但是，每种因素对于最终幸福指数的影响一般是不同的：大多数人可能希望拿比较多的工资，但是工资过高可能意味着额外的负担；人们对可自由支配的时间，可能比对人口密度更加敏感……

我们不妨把这几个因素单独列出来，看看它们各自对幸福指数的影响：

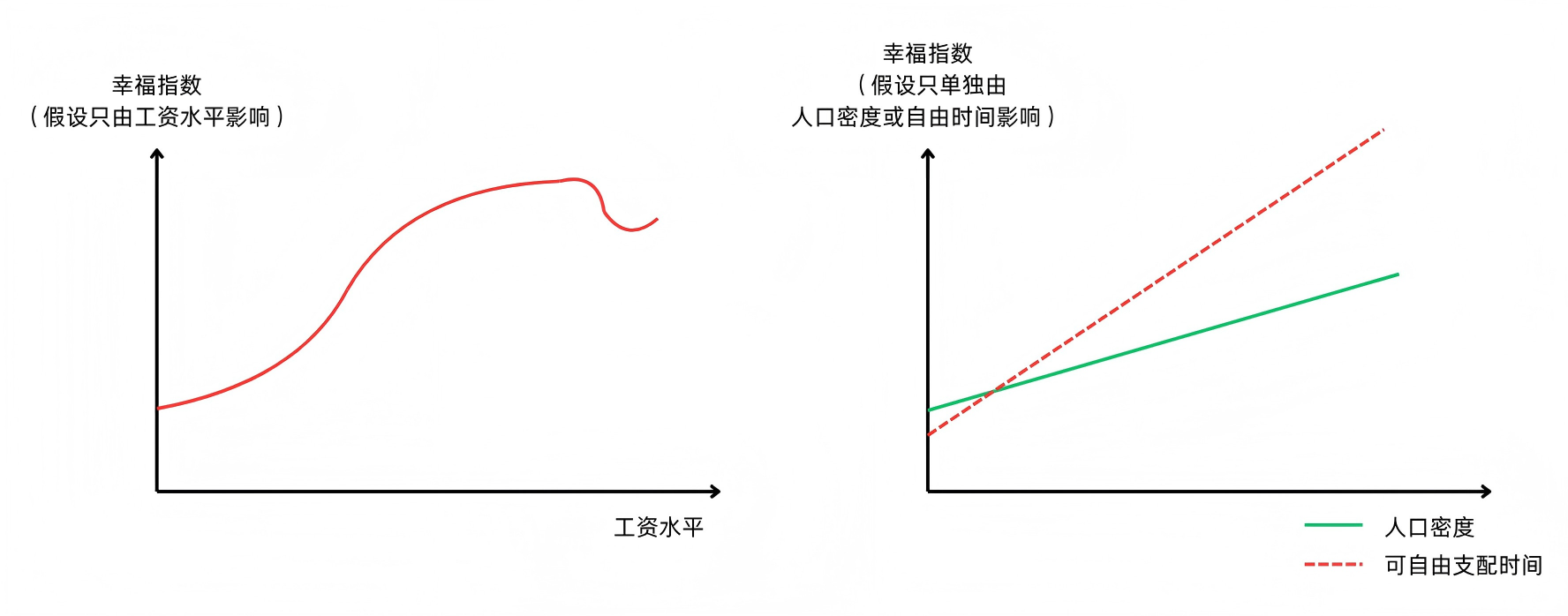
我们可以看到，假设其他条件都不变，工资水平越高，并不意味着幸福指数就越高。此外，有些因素（比如可自由支配时间）可能比其他因素（比如人口密度）更让人敏感

2.3 回到机器学习

而当我们做机器学习时，往往需要处理成百上千、甚至百万级以上量级的不同“因素”

这些“因素”对应的就是上面公式里的x，也就是特征向量

而人们对每个“因素”有多“敏感”，就是用和x相乘的θ，也就是特征权重来表示的

在线性模型中，我们就假设每个因素对最终结果的影响都是线性的，如果在二维图表上表示，那它们就都是直线，就像第二张图一样（而不是第一张图这种曲线）

所以幸福指数，就可以表示为这样一个线性模型：幸福指数 = 偏置值 + 工资水平的影响程度 * 工资水平 + 人口密度的影响程度 * 人口密度 + 可自由支配时间的影响程度 * 可自由支配时间 + ……

幸福指数 = 偏置值 + 工资水平的影响程度 * 工资水平 + 人口密度的影响程度 * 人口密度 + 可自由支配时间的影响程度 * 可自由支配时间 + ……

这里的偏置值，就是给整体幸福指数加一个值做微调。我们还是可以用二维图像来举例：

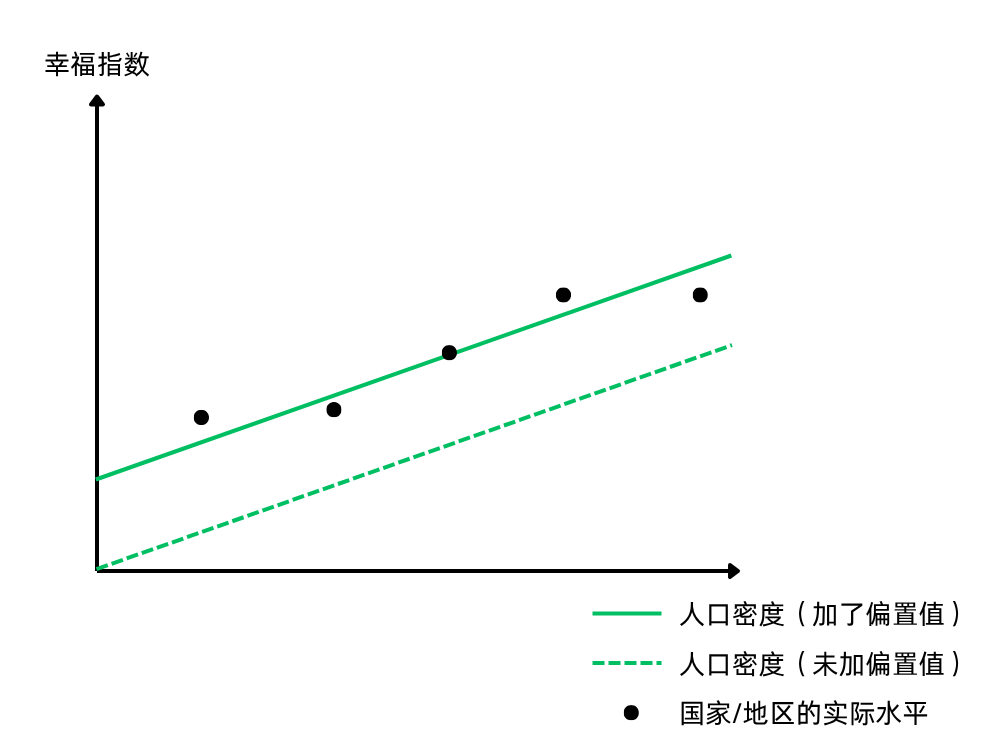
这就像一元一次函数的直线，用y=kx+b表示（初中学过，是不是更熟悉？），偏置值就是这个b，不加的话，直线就一定会经过原点，而这在绝大多数情况下都是不符合我们的期望的

有了每个特征值的权重，只能影响这条直线的“斜率”k，但是我们还需要根据实际的数据所在位置，加上这个偏置值b来微调

【注意】如果参数数量增多，就不能用二维图像来表示了，可能是三维甚至更高维。但是偏置值的概念是不会变的

2.4 从几何意义看：向量是怎么回事？

有人要问了：“你这边说的都是方程、是一元一次或者二元一次函数的图像；但你刚刚又说什么特征向量，这和向量有什么关系？”

很好，到这一步，说明你真正开始探索机器学习的几何意义了，也就是如何更加直观地表示“我如何让模型预测结果更加接近我的目标”

我们还是用“人口密度”和“可自由支配时间”这两个因素来举例说明，假设只有这两个因素决定了一个国家的幸福指数，它实际上可以用一个向量表示：

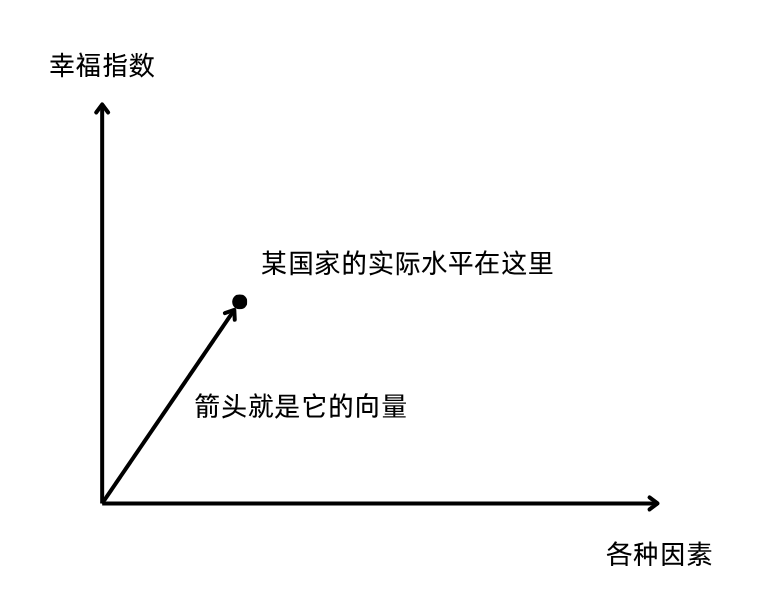
还记得人们对“人口密度”和“可自由支配时间”两个因素的“敏感度”是不一样的吧？体现在图像上，它们两者的斜率肯定也是不同的

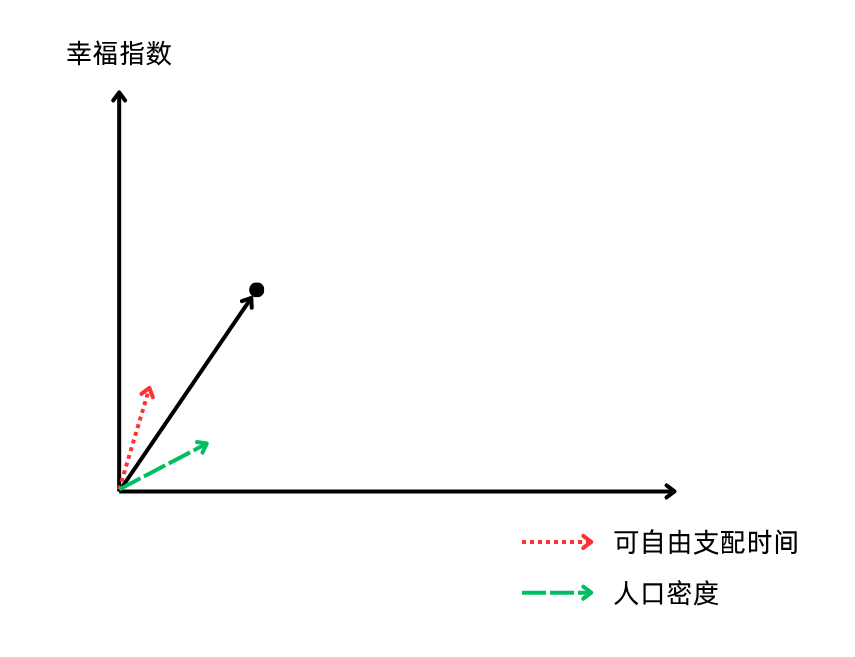
这里，“人口密度”和“可自由支配时间”两个因素，分别由两个斜率不同的向量箭头表示，长度均为1（这也叫单位向量）

从几何意义上理解，我们要做的其实是找到多少个“人口密度”的向量+多少个“可自由支配时间”的向量，最终可以得到这个国家实际幸福指数水平的向量！

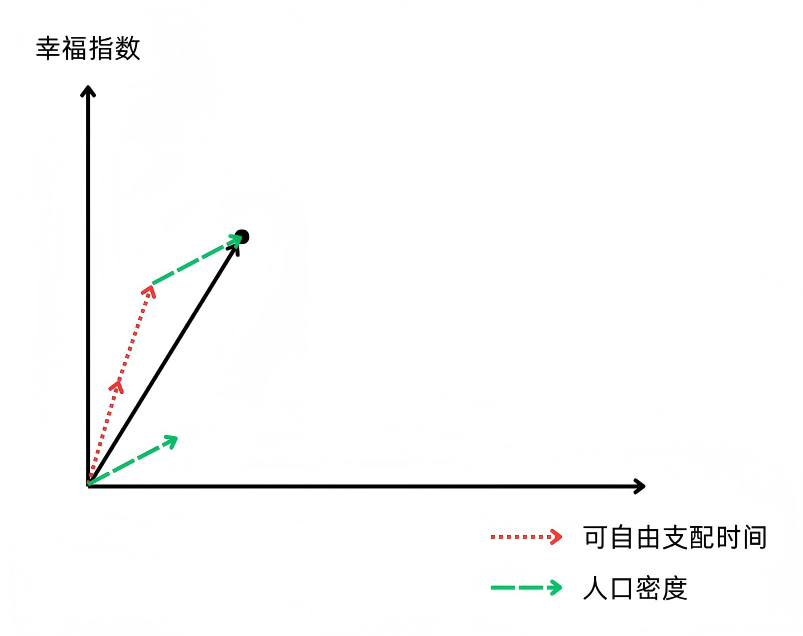
我们发现，1个“人口密度”的单位向量+2个“可自由支配时间”的单位向量，最终能得到这个国家实际幸福指数的向量。也就是说，在这个线性模型中，θ1 = 1（人口密度对应的特征权重），θ2 = 2（可自由支配时间对应的特征权重）

我们在机器学习中建立线性模型的目标，其实就是找到每个特征分别给多少权重（也就是每个特征向量分别要乘多少数量），才能得到最接近实际的预测结果

即使参数在更复杂的模型里会变得更多，可能无法用简单的二维图像来表示，但是原理其实是一样的

【注意】我个人感觉，用几何意义来理解这一块内容，比起纯代数会更加直观。如果之后想到更好的讲述方法，我会更新在这一块

如果用向量来表示的话，由于θ和x通常都是2行1列的二维矩阵，计算时需要将θ向量进行转置（transpose），用1行2列和2行1列的向量相乘才能计算

2.5 训练模型：最小化误差

如何训练一个模型呢？我们是要让模型的预测结果尽可能接近实际结果，也就是误差尽量要小

在实操中，我们会使用均方误差（mean square error）来衡量这个误差，相比均方根差（root mean square error）会更加方便。因为后者还要求平方根，而且二者的结果只从大小比较上看是一致的*

*因为误差的大小一定是正数，因此，比如4的平方根取2，9的平方根取3，4 < 9，2 < 3，判断大小的结果是一致的，所以没必要再求平方根了

均方误差的计算公式如下：

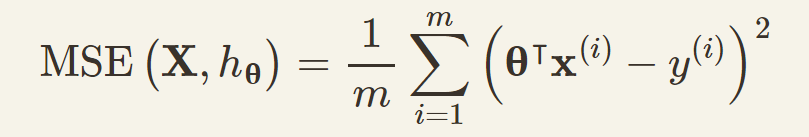
其实这个公式的含义就是：获取每个实例特征向量和特征权重向量相乘的结果（也就是模型预测的结果），减去对应的实际结果，再求平方。把所有的平方求和，就是要求的均方误差

例如：预测值是10、12、13，对应实际结果是11、14、12，那么均方误差就等于：

(10-11)^2 + (12-14)^2 + (13-12)^2 = 6

因此，对数学公式不熟悉或者感到害怕的朋友们也不用担心，我们只需要理解它背后的含义就好了，公式只是一种抽象化的表达

2.6 正规方程

在训练过程中，我们知道每个实例传入的特征向量x，也知道对应的实际结果y，要求的或者说要优化的，其实就是θ这个特征权重向量

怎么求呢？其实，数学上是有公式来求这个让均方误差最小的θ的，这叫作正规方程（normal equation），也叫法方程：

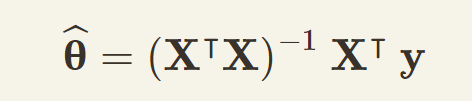
X表示训练集里所有的训练数据，上标T表示转置，上标-1表示逆矩阵，y表示训练集里所有结果。如果(X^T X)可逆，那这里的结果就是最优解

在Python中对一个训练集求正规方程解的步骤，请参考3.1 正规方程的Python计算

当然，我们有比正规方程更简便的Python实现方式：运用线性回归LinearRegression。这里的代码同样可以参考3.1 正规方程的Python计算

2.6.1 正规方程和线性回归的区别

线性回归使用的是摩尔-彭若斯广义逆矩阵，它运用了一种奇异值分解（singular value decomposition, SVD）的方法，太复杂的数学原理不做阐述，只讲它在这里的作用：

1. 比起计算正规方程，它的代码更加简单高效

2. 它可以处理(X^T X)不可逆的情况

不仅如此，使用正规方程和线性回归，计算的复杂度也不同：前者求逆矩阵的复杂度一般为O(n^2.4)到O(n^3)，而后者为O(n^2)

这两种方法面对训练数据的增长，它们的计算复杂度的增长也是线性的；但是如果参数的数量大幅增多，它们的效率就比较低了

【原因】这是因为计算量最大的是求(X^T X)的逆矩阵这个过程。如果只是增加训练数据，那其实就是增加行数m，复杂度也就是O(m)；但如果增加了参数的数量，就相当于增加列数n，求逆矩阵的复杂度就会变成O(n^2)甚至O(n^3)

2.6.2 补充概念：复杂度

关于复杂度的详细概念，可以参考平台上其他文章，很多写得很详细。简而言之，它是一个衡量算法计算复杂程度的标准。在此我先把常见的复杂度按照从小到大排列一下：

常数阶O(1) < 对数阶O(logN) < 线性阶O(n) < 线性对数阶O(nlogN) < 平方阶O(n^2) < 立方阶O(n^3) < K次方阶O(n^k) < 指数阶(2^n)

很明显，O(m)这个线性阶的复杂度，要比O(n^2)或者O(n^3)这样的平方或立方阶低得多，计算机也就只需要花少得多的时间和资源来计算

那如果参数数量急剧增加怎么办？我们有另一种方法：梯度下降

2.7 梯度下降（Gradient Descent）

梯度下降是一种通用的优化算法，能够为各种各样的问题找到最优解。梯度下降的基本思想是通过迭代调整参数来最小化代价函数。

又要看晕了。还好，这次Geron也举了个例子：

比如你在山里遇到了大雾，看不到任何东西。这时候一种下山的方式就是感知你脚下的四周，看看哪条路是最陡峭、最快下山的。每走一步就往四周这样看一遍走一步，直到走到一个最低点：四周没有比脚下更低的路了

这就是梯度下降：它会测量误差函数相对于参数权重向量θ的局部“梯度”（可以理解为山的陡峭程度），并朝着梯度下降的方向前进。一旦梯度为零（路面平了，四周都是上山的路），就达到了最小值

可以参考原书中的图示：

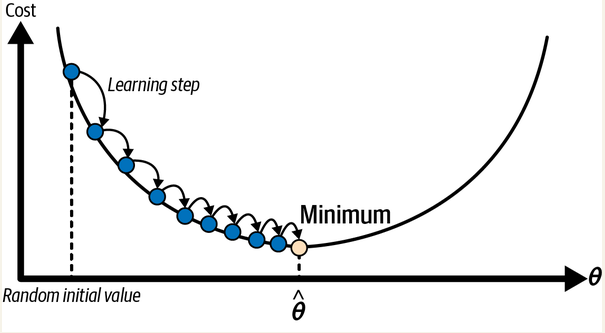
但是，这“每一步”，要跨多大？这也是机器学习算法很重要的一个点。这个步子的大小有一个专有术语：学习率（learning rate）

如果每步太大，算法可能会发散，相当于从山的一侧直接跨到了另一侧更高的位置

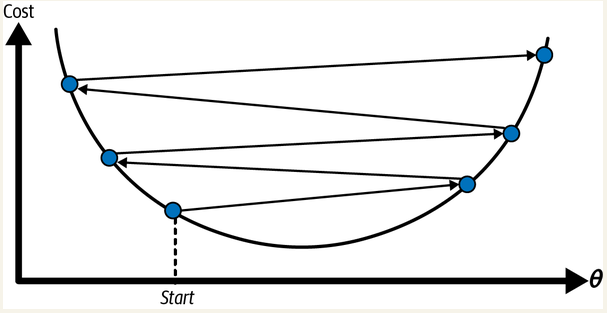
如果每步太小，算法就需要走很多步才能找到最小值

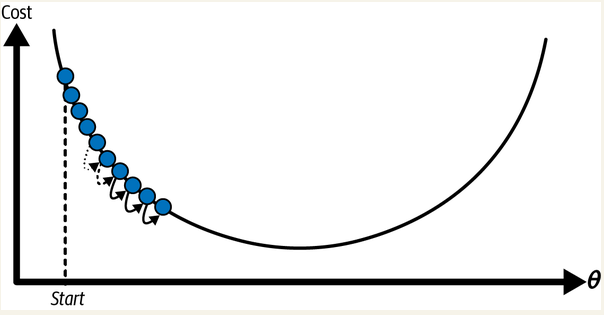
而且，实际场景下算法遇到的“山”，几乎肯定不会像上面的图一样如此规则：这座山可能有各种沟壑、凸起。我们看下面这张图，就能发现另外的问题：

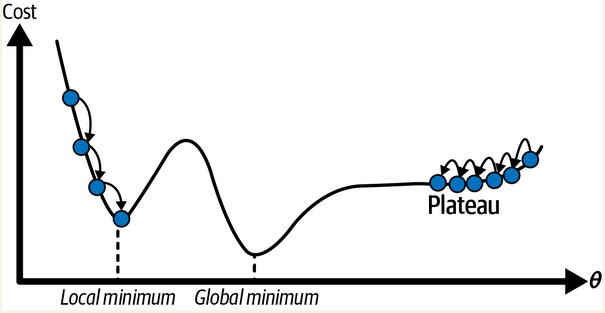
如果从左边这条路往下走，最终可能会走到一个“局部最低点”，但是无法走到“全局最低点”

如果从右边这条路走，那可能要走很久才能走到“全局最低点”

好在，均方误差对线性回归求成本函数，图像是一个凸函数（convex function）。这种函数图像上任意两点连线的中点一定在函数曲线及曲线以上的位置。因此，它没有局部最小值，通过梯度下降一定能找到它的全局最小值

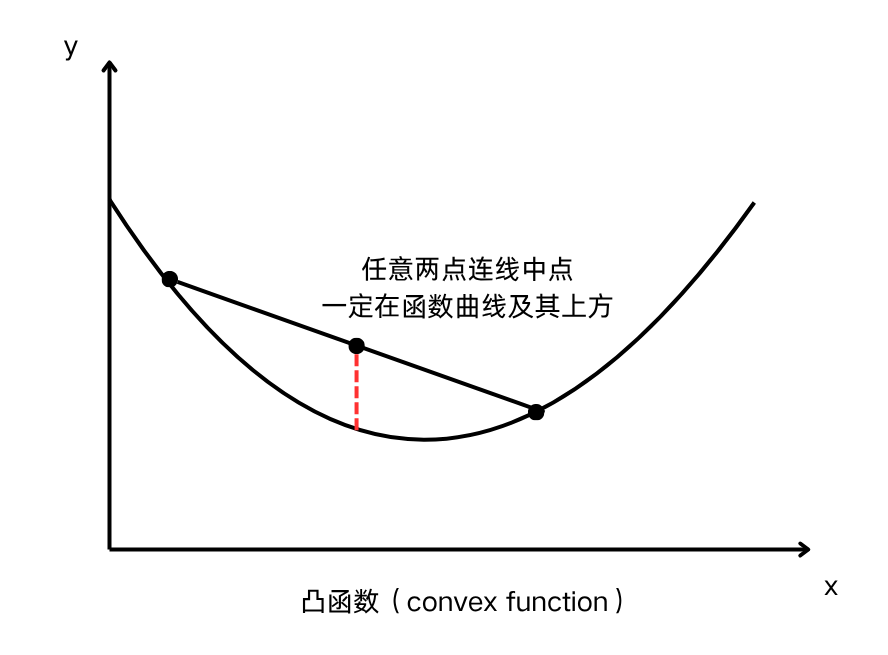
【注意】凸函数在这里指的是向下凸的函数

3. 代码实践与实验流程

3.1 正规方程的Python计算

# 1. Test the normal equation in Python
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(42)  # to make this code example reproducible
m = 100  # number of instances
X = 2 * np.random.rand(m, 1)  # column vector
y = 4 + 3 * X + np.random.randn(m, 1)  # column vector
plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', alpha=0.6, label='Data points')
plt.title("Scatter Plot of X vs y")
plt.xlabel("X")
plt.ylabel("y")
plt.legend()
plt.grid(True)
plt.show()

图像如下：

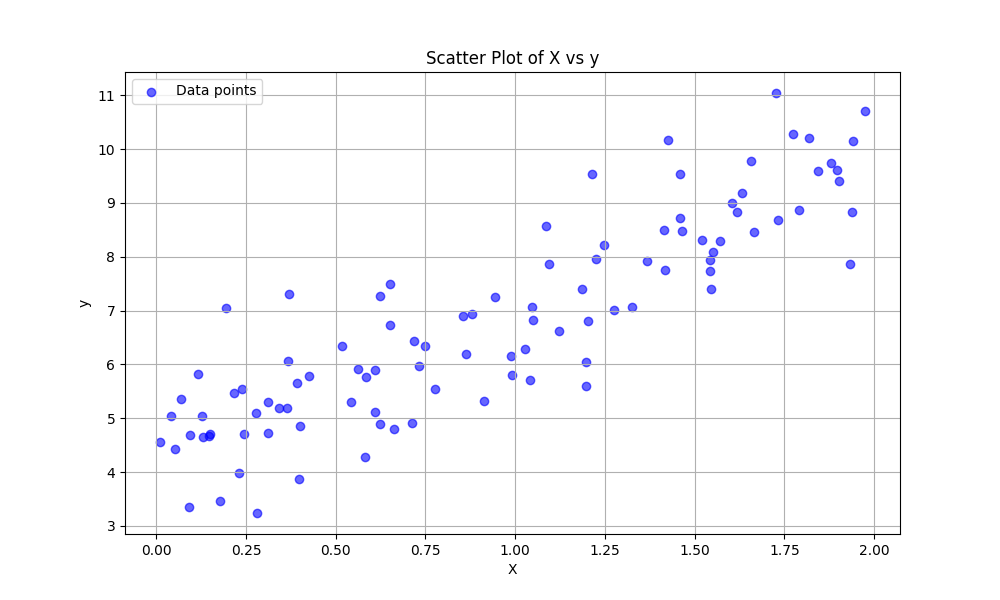
接下来，我们就通过正规方程求出最佳的θ：

# Next, to calculate the normal equation
from sklearn.preprocessing import add_dummy_feature
X_b = add_dummy_feature(X)  # add x0 = 1 to each instance
theta_best = np.linalg.inv(X_b.T @ X_b) @ X_b.T @ y
print("With normal equation, the best θ is: ", theta_best)
# Output: With normal equation, the best θ is:  [[4.21509616]
# [2.77011339]]

我们发现，虽然原先的y是4+3X，我们预想的θ最佳值应该是[[4] [3]]，但是因为加入了噪声，使得实际求出的值发生了偏移

接下来我们就可以用求出的θ来做预测了：

X_new = np.array([[0], [2]])  # Create a vector
X_new_b = add_dummy_feature(X_new)  # Add a column with all 1s, so that it is allowed to add the bias term
y_predict = X_new_b @ theta_best
print("For the new example, the predicted value is: ", y_predict)
# Output: For the new example, the predicted value is:  [[4.21509616]
#  [9.75532293]]
plt.figure(figsize=(9, 6))
plt.scatter(X, y, color="#1f77b4", alpha=0.7, edgecolor='white', s=70, label="Training data")
plt.plot(X_new, y_predict, "r-", linewidth=2.5, label="Regression line")

# Highlight the predicted points
plt.scatter(X_new, y_predict, color="red", s=80, edgecolor='black', zorder=5)
for i, (x_val, y_val) in enumerate(zip(X_new.flatten(), y_predict.flatten())):
    plt.text(x_val + 0.05, y_val, f"({x_val:.1f}, {y_val:.2f})", fontsize=10, color="darkred")

# Titles and labels
plt.title("Prediction using Normal Equation", fontsize=14, pad=15)
plt.xlabel("X (input feature)", fontsize=12)
plt.ylabel("y (target value)", fontsize=12)

# Add grid, legend, and style tweaks
plt.legend(fontsize=11)
plt.grid(True, linestyle="--", alpha=0.5)
plt.tight_layout()

plt.show()

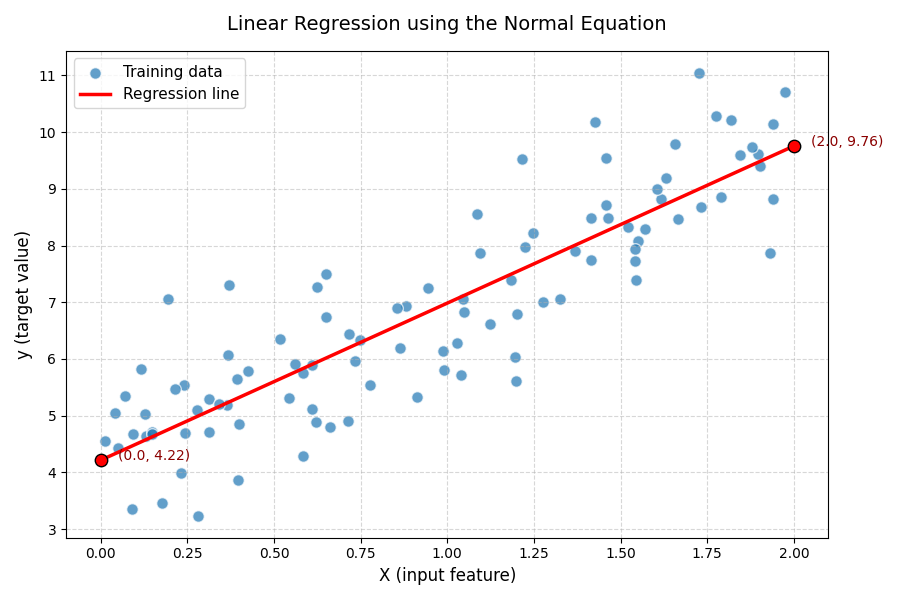
根据计算得出的θ，最终它生成的线性模型，应该是图中红线所示的这一条

当然，我们还可以用前面讲过的线性回归（LinearRegression）来计算θ的最优解，并用它做预测，这会更加简单直接：

# Alternatively, we could use LinearRegression to calculate the best θ, and make predictions
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
print("We could get the θ: ", lin_reg.intercept_, lin_reg.coef_)
# Output: We could get the θ:  [4.21509616] [[2.77011339]]
# This is the same result as using normal equation
print("Use linear regression to predict, the result is: ", lin_reg.predict(X_new))
# Output: Use linear regression to predict, the result is:  [[4.21509616]
#  [9.75532293]]