【浅水模型MATLAB】尝试完成一个数值模拟竞赛题

更新于2024年6月8日

前言

最近看到第四届水科学数值模拟创新大赛的通知，就好奇翻看了前几年的比赛试题。发现去年的一个试题十分有趣，而且实现难度不是很大。因此，想着自己动手，从零开始学一下原理、做一下模型、编一下代码。

由于本人平时用Matlab较多，且Matlab代码可读性较强，容易与数学公式联系。所以，以下代码部分均用的Matlab。
如果你习惯别的代码，也想做类似的建模尝试，十分欢迎一起交流！（最近有点想转python代码了，希望感兴趣的同志来一起交流）
如果各位朋友发现了文章或代码中的错误，亦或是改进之处，请不吝赐教，欢迎大家留言，一起改进模型！本博客文章将持续更新，上面也会标注提出改进建议的同志们。（不过，本人最近在忙活毕业论文，可能更新不及时）

同时，想要完整代码的朋友请联系我，我可无偿提供脚本文件。

希望同大家一起进步！

通知链接：关于公布第三届水科学数值模拟创新大赛复赛试题的通知
题目链接：河道水动力模拟（青年组）.pdf

题目描述

某浅水湖泊承担着涵养水源、净化环境、调节径流、维护区域生物多样性等多种重要的水安全保障功能。由于该湖泊地处平原地带，湖体局部水动力条件微弱，需通过有限的外调水量增强湖泊整体水动力，实现活水提质。
研究湖泊为矩形平底浅水湖泊，长L = 10km，宽 W = 5km，糙率为n = 0.02（Manning系数）；该湖泊通过3个入口与1个出口与外部河道连通，入口及出口口门宽均为100m；3个入口总入湖流量为 100m³/s，出口水位为2.0m；多年监测数据表明，该湖泊东北区约占整个湖体 1/4 面积大小的区域（下图阴影区域）水动力偏弱，需通过调控入口流量增强该区水动力。

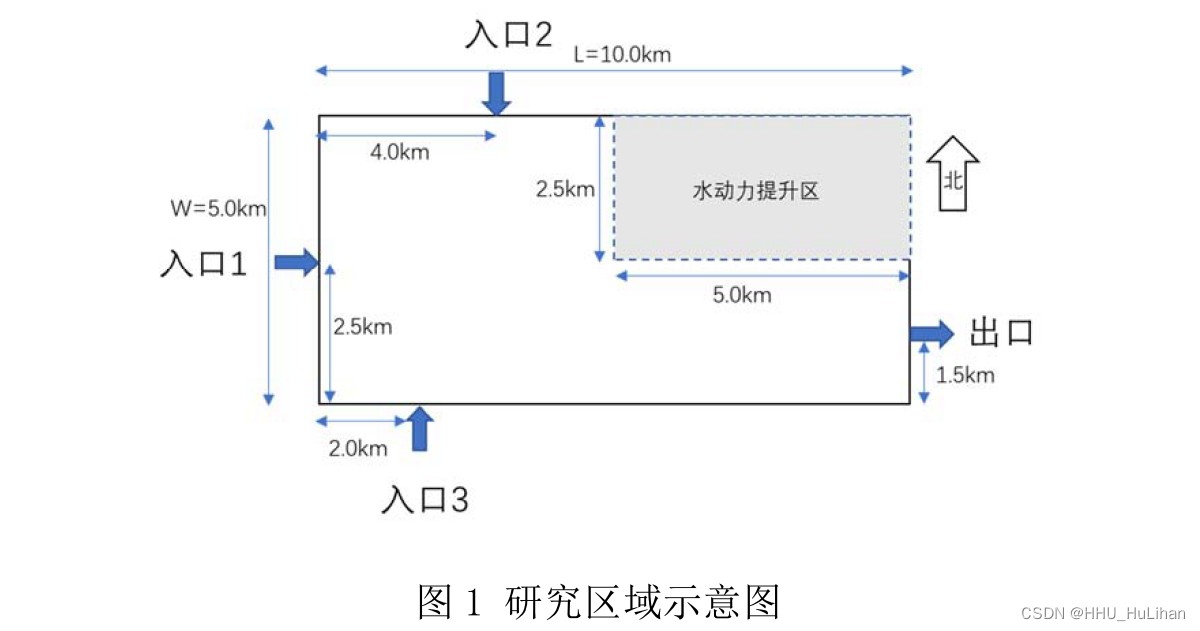
问题分析

根据题目描述，我们可以设计一个二维浅水方程模型（垂向平均水动力方程）。涉及到的边界条件包括入流边界条件、水位边界条件。
其次，模型的计算域是一个简单的矩形。因此，我们可以采用结构化矩形网格和笛卡尔坐标系。同时，这样的处理方式简化了建模过程。
此外，计算区域中没有浅滩，所有的区域水深都大于0，即没有干-湿边界的问题。这也简化了问题本身，简化了建模过程。

设计模型的思路如下：

1. 设计一个二维浅水方程的求解器，通过一个简单的溃坝算例测试其性能（也可以从一维浅水方程求解器开始，这样更为简单）；
2. 尝试加入两种边界条件，使其正常运行；
3. 根据上图要求，完成整个模型。

本博文内容就省略前面两个步骤了，直接描述如何构建整个模型。但是，我也确实进行了前两个步骤，我认为对于模型开发而言，前两个步骤是十分必要的。

理论基础

在原理上，我参考了Liang等¹的数值模拟研究。他们的模型采用了有限体积法，以Godunov型方法为框架，求解了适应复杂地形并保持良好平衡特性的二维浅水方程。

控制方程

矩阵形式的浅水方程如下：
$$\begin{gathered} \frac{\partial \mathbf{U}}{\partial t}+\frac{\partial \mathbf{F}(\mathbf{U})}{\partial x}+\frac{\partial \mathbf{G}(\mathbf{U})}{\partial y}=\mathbf{S}(\mathbf{U}) \\ \mathbf{U}=\left(\begin{array}{c}h\\ hu\\ hv\end{array}\right),\mathbf{F}(\mathbf{U})=\left(\begin{array}{c}hu\\ h{u}^2+\frac{g{h}^2}{2}\\ huv\end{array}\right),\mathbf{G}(\mathbf{U})=\left(\begin{array}{c}hv\\ huv\\ h{v}^2+\frac{g{h}^2}{2}\end{array}\right), \\ \mathbf{S}(\mathbf{U})=\left(\begin{array}{c}0\\ -\frac{{\tau }_{bx}}{\rho }-gh\frac{\partial z_b}{\partial x}\\ -\frac{{\tau }_{by}}{\rho }-gh\frac{\partial z_b}{\partial y}\end{array}\right) \end{gathered}$$
式中，$h$表示水深，$\eta$表示水位，$u$、$v$分别表示两个方向的水平流速，$z_b$表示底高程，$\rho$表示水体密度；切应力$\tau$的表达式：
$$\begin{gathered} {\tau }_{bx}=\rho C_{f}u\sqrt{u^2+v^2} \\ {\tau }_{by}=\rho C_{f}v\sqrt{u^2+v^2} \\ {C}_f=g{n}^2{h}^{1/3} \end{gathered}$$
式中，n表示Manning系数。水位η、水深h及水底高程z_b的相对关系是：
$$\eta =h+z_b$$

由于传统的Godunov型有限体积法不能保证水体在静止状态时压力与底坡源项的平衡，即会在静水条件下产生虚假流动。因此，Liang等改进了上述方程，得到了如下的平衡形式：
$$\begin{gathered} \mathbf{U}=\left(\begin{array}{c}\eta \\ hu\\ hv\end{array}\right),\mathbf{F}(\mathbf{U})=\left(\begin{array}{c}hu\\ h{u}^2+\frac{1}{2}g({\eta }^2-2\eta z_b)\\ huv\end{array}\right), \\ \mathbf{G}(\mathbf{U})=\left(\begin{array}{c}hv\\ huv\\ h{v}^2+\frac{1}{2}g({\eta }^2-2\eta z_b)\end{array}\right),\mathbf{S}(\mathbf{U})=\left(\begin{array}{c}0\\ -\frac{{\tau }_{bx}}{\rho }-g\eta \frac{\partial z_b}{\partial x}\\ -\frac{{\tau }_{by}}{\rho }-g\eta \frac{\partial z_b}{\partial y}\end{array}\right) \end{gathered}$$
上述这个方程组就是我们的模型的基础！

数值方法

首先，我们将u、v、h等物理量定义在网格的中心。从左至右，网格的编号依次为i = 1,2,3, …, M；从下至上，网格的编号依次为j = 1,2,3, …, N。因此，网格中心的坐标写作$x_{i,j}$和$y_{i,j}$，网格大小可写作$\Delta x_i=x_{i+1/2}-x_{i-1/2}$和$y_j=y_{j+1/2}-y_{j-1/2}$。
在时间域上，模型采用二阶龙格库塔格式。已知n时间步的水力变量${\mathbf{U}}^n$，则下一时间步的${\mathbf{U}}^{n+1}$为：
$$\begin{gathered} \frac{{\mathbf{U}}^{(1)}-{\mathbf{U}}^n}{\Delta t}=-(\frac{\partial \mathbf{F}}{\partial x}+\frac{\partial \mathbf{G}}{\partial y}{)}^n+{\mathbf{S}}^n \\ \frac{{\mathbf{U}}^{(2)}-{\mathbf{U}}^{(1)}}{\Delta t}=-(\frac{\partial \mathbf{F}}{\partial x}+\frac{\partial \mathbf{G}}{\partial y}{)}^{(1)}+{\mathbf{S}}^{(1)} \\ {\mathbf{U}}^{n+1}=\frac{1}{2}({\mathbf{U}}^n+{\mathbf{U}}^{(2)}) \end{gathered}$$
式中的$\Delta t$表示时间步长，它是通过CFL条件来确定的；每一次时间步进时，$\Delta t$的计算过程如下：
$$\begin{gathered} \Delta t=Cmin(\Delta t_x,\Delta t_y) \\ \Delta t_x=min[\frac{\Delta x_i}{|u_i|+\sqrt{g{h}_i}}] \\ \Delta t_y=min[\frac{\Delta y_j}{|v_j|+\sqrt{g{h}_j}}] \end{gathered}$$
式中，C表示Courant数字；数值计算稳定的必要条件是C<1.0。一般的，C取0.5~0.75。对于时间步进式中的通量导数项，它的离散形式如下：
$$\begin{gathered} \frac{\partial \mathbf{F}}{\partial x}=\frac{{\mathbf{F}}_{i+1/2,j}-{\mathbf{F}}_{i-1/2,j}}{\Delta x} \\ \frac{\partial \mathbf{G}}{\partial y}=\frac{{\mathbf{G}}_{i,j+1/2}-{\mathbf{G}}_{i,j-1/2}}{\Delta y} \end{gathered}$$
在求解网格边界(i+1/2, j)和(i, j+1/2)处的通量时，需要通过一个局部黎曼问题的求解器，以确定网格边界处的通量F和G。在此，我们选择HLL求解这个局部黎曼问题。对于网格边界处的水位、水深、流速等物理量的值，我们则通过分段线性重构的方式得到。

分段线性重构可以得到一个边界左右（或上下）两侧的物理量值。分段线性重构的数学表达式如下：
$$\begin{gathered} U_{i+1/2,j}^L=U_{i,j}+\frac{\Delta x_i}{2}Lim(\frac{U_{i,j}-U_{i-1,j}}{x_i-x_{i-1}},\frac{U_{i+1,j}-U_{i,j}}{x_{i+1}-x_i}) \\ {U}_{i+1/2,j}^R=U_{i+1,j}-\frac{\Delta x_{i+1}}{2}Lim(\frac{U_{i+1,j}-U_{i,j}}{x_{i+1}-x_i},\frac{U_{i+2,j}-U_{i+1,j}}{x_{i+2}-x_{i+1}}) \\ {U}_{i,j+1/2}^L=U_{i,j}+\frac{\Delta y_j}{2}Lim(\frac{U_{i,j}-U_{i,j-1}}{y_j-y_{j-1}},\frac{U_{i,j+1}-U_{i,j}}{y_{j+1}-y_j}) \\ {U}_{i,j+1/2}^R=U_{i,j+1}-\frac{\Delta y_{j+1}}{2}Lim(\frac{U_{i,j+1}-U_{i,j}}{y_{j+1}-y_{j+1}},\frac{U_{i,j+2}-U_{i,j+1}}{y_{j+2}-y_{j+1}}) \end{gathered}$$
式中的U可以表示水位、水深、流速等任一物理量，Lim则表示斜率限制器。为了保持数值稳定，本模型采用了minmod限制器：
$$minmod(a,b)=\{\begin{array}{ll}0,& ab\le 0\\ min(|a|,|b|),& ab>0\end{array}$$

在通过斜率限制器进行分段线性重构后，得到了网格边界的水位、水深、流速，也计算出了网格边界处的通量F_L、F_R、G_L和G_R。之后通过HLL求解器得到网格边界处的F和G。下面以x方向为例，列出HLL求解器的表达式：
$$\begin{gathered} \mathbf{F}=\{\begin{array}{ll}{\mathbf{F}}_L,& s_L\ge 0\\ {\mathbf{F}}^{\ast },& s_L<0<s_R\\ {\mathbf{F}}_R,& s_R\le 0\end{array} \\ {\mathbf{F}}^{\ast }=\frac{s_R{\mathbf{F}}_L-s_L{\mathbf{F}}_R+s_L{s}_R({\mathbf{U}}_R-{\mathbf{U}}_L)}{s_R-s_L} \\ {s}_L=min(u_L-\sqrt{g{h}_L},u_s-\sqrt{g{h}_s}) \\ {s}_R=min(u_R+\sqrt{g{h}_R},u_s+\sqrt{g{h}_s}) \\ {u}_s=\frac{1}{2}(u_L+u_R)+\sqrt{g{h}_L}-\sqrt{g{h}_R} \\ \sqrt{g{h}_s}=\frac{\sqrt{g{h}_L}+\sqrt{g{h}_R}}{2}+\frac{u_L+u_R}{4} \end{gathered}$$

边界条件

本模型涉及了三边界条件，一是入流边界，二是水位边界，三是固壁边界（采用free-slip边界）。这两个边界的在《【CFD小工坊】浅水模型的边界条件》中有介绍。
我们以右侧边界M+1/2为例，此网格左侧水深h_L、法向流速u_L，以及右侧水深h^* 、法向流速u^*满足：
$$\begin{gathered} u_L+2c_L=u^{\ast }+2c^{\ast } \\ {c}_L=\sqrt{g{h}_L},c^{\ast }=\sqrt{g{h}^{\ast }} \end{gathered}$$
当采用流量边界时，右侧网格的单宽流量q被指定，即$q=h^{\ast }{u}^{\ast }$已知，则有：
$$u_L+2c_L=u^{\ast }+2c^{\ast }=\frac{q}{h^{\ast }}+2\sqrt{g{h}^{\ast }}=\frac{q}{{c^{\ast }}^2/g}+2\sqrt{g{h}^{\ast }}$$
化简后，上述方程为$c^{\ast }$的一元三次方程：
$$2{c^{\ast }}^3-(u_L+2\sqrt{g{h}_L}){c^{\ast }}^2+gq=0$$
求出方程c^*后，所有的物理量都能被指定。

对于水位边界，边界处的h^*被指定，则有
$$u^{\ast }=u_L^{\ast }+2c_L-2c^{\ast }=u_L^{\ast }+2\sqrt{g{h}_L}-2\sqrt{g{h}^{\ast }}$$

对于固壁边界，法向速度和通量被定义为0。在求解过程中，可设置h^* = h_L。

代码框架与关键代码

我的模型代码主要分为五个部分：

1. 参数设置：设置物理参数、网格参数、时间参数等。代码如下所示：

grav = 9.81;            % Gravitational acceleration
rho = 1000;             % Density
CFL = 0.5;              % Courant Number

Lx = 10000;             % Length of the domain
Ly = 5000;              % Width of the domain
n = 0.02;               % Manning coefficient

zb0 = 0.0;              % Bottom elevation
eta0 = 2.0;             % Initial water elevation
h0 = 2.0;               % Initial water depth

dx = 25;                % Grid spacing
dy = 25;                % Grid spacing
dt = 0.2;               % Time spacing at the first step
dtmax = 4.0;            % allowed max time step (s)
tend = 3600;            % End of the simulation time
plot_int = 60;          % Time interval to next plot

Q_in = 100;             % Total discharge of the inlets
eta_out = 2.0;          % Specified water level of the outlet

我设置网格为边长25m的正方形，底高程为zb0=0.0，初始水位与出口水位一致，即eta0 = 2.0。Courant数设置为0.5，初始时间步为0.2s，之后的每一个时间步通过CFL条件计算得到。

2. 网格构建：网格有两个要素需要定义，一是网格的四个节点（Xp和Yp），二是网格的中心点（Xc和Yc）；网格中心点也即水力物理量定义的位置。

%% Construct the grid
Nx = Lx/dx;     Ny = Ly/dy;
xp = [0:dx:Lx];         % Points
yp = [0:dy:Ly];
xc = [0.5:dx:Lx];       % Cell centers
yc = [0.5:dy:Ly];
[Xp Yp] = meshgrid(xp, yp);
[Xc Yc] = meshgrid(xc, yc);

3. 初始化：设置底高程zb，计算zb的梯度zbx和zby；之后再设置初始流速u、v为零。

%% Initialization
zbc = zb0 * ones(Ny,Nx);
zbp = zb0 * ones(Ny+1,Nx+1);

zbx = (0.5*(zbp(1:end-1,2:end)+zbp(2:end,2:end)) - ...
       0.5*(zbp(1:end-1,1:end-1)+zbp(2:end,1:end-1)) ) /dx;
zby = (0.5*(zbp(2:end,1:end-1)+zbp(2:end,2:end)) - ...
       0.5*(zbp(1:end-1,1:end-1)+zbp(1:end-1,2:end)) ) /dy;

eta = eta0 * ones(Ny,Nx);
h = eta - zbc;
u = zeros(Ny,Nx);       v = zeros(Ny,Nx);

4. 主循环：（1）计算网格边界处的水位、水深、流速值；（2）设置边界条件；（3）计算通量项F_L、F_R、G_L和G_R；（4）利用HLL求解通量F和G；（5）计算源项S；（6）计算新一个时间步的eta、h、u和v。

%% Main Loop
t = 0;
tplot = 0;
while(t<tend)
    % estimate the dt
    dtx = dx./(abs(u)+sqrt(grav*h) + 1E-8);
    dty = dy./(abs(v)+sqrt(grav*h) + 1E-8);
    dt1 = min(min(dtx,[],"all"), min(dty,[],"all"));
    dt = min(dtmax, CFL*dt1);
    clear dt1 dtx dty
    
    etan = eta;     hn = h;
    un = u;         vn = v;
    % 2rd-order Runge-Kutta Method
    for k = 1:2
        % 1. reconstruct the flow data
        % 1.1 x-direction reconstruction (Natural closed boundary)
        e_ = [eta(:,1), eta, eta(:,end)];
        u_ = [u(:,1), u, u(:,end)];
        v_ = [v(:,1), v, v(:,end)];
        de = minmod((e_(:,3:end)-e_(:,2:end-1))/dx, ...
                    (e_(:,2:end-1)-e_(:,1:end-2))/dx);
        du = minmod((u_(:,3:end)-u_(:,2:end-1))/dx, ...
                    (u_(:,2:end-1)-u_(:,1:end-2))/dx);
        dv = minmod((v_(:,3:end)-v_(:,2:end-1))/dx, ...
                    (v_(:,2:end-1)-v_(:,1:end-2))/dx);
        exL = [eta(:,1), eta+0.5*dx*de];
        exR = [eta-0.5*dx*de, eta(:,end)];
        hxL = exL - 0.5*(zbp(1:end-1,:) + zbp(2:end,:));
        hxR = exR - 0.5*(zbp(1:end-1,:) + zbp(2:end,:));
        uxL = [u(:,1), u+0.5*dx*du];
        uxR = [u-0.5*dx*du, u(:,end)];
        vxL = [v(:,1), v+0.5*dx*dv];
        vxR = [v-0.5*dx*dv, v(:,end)];
        clear e_ u_ v_ de du dv
        % 1.2 y-direction reconstruction (Natural closed boundary)
        e_ = [eta(1,:); eta; eta(end,:)];
        u_ = [u(1,:); u; u(end,:)];
        v_ = [v(1,:); v; v(end,:)];
        de = minmod((e_(3:end,:)-e_(2:end-1,:))/dy, ...
                    (e_(2:end-1,:)-e_(1:end-2,:))/dy);
        du = minmod((u_(3:end,:)-u_(2:end-1,:))/dy, ...
                    (u_(2:end-1,:)-u_(1:end-2,:))/dy);
        dv = minmod((v_(3:end,:)-v_(2:end-1,:))/dy, ...
                    (v_(2:end-1,:)-v_(1:end-2,:))/dy);
        eyL = [eta(1,:); eta+0.5*dy*de];
        eyR = [eta-0.5*dy*de; eta(end,:)];
        hyL = eyL - 0.5*(zbp(:,1:end-1) + zbp(:,2:end));
        hyR = eyR - 0.5*(zbp(:,1:end-1) + zbp(:,2:end));
        uyL = [u(1,:); u+0.5*dy*du];
        uyR = [u-0.5*dy*de; u(end,:)];
        vyL = [v(1,:); v+0.5*dy*dv];
        vyR = [v-0.5*dy*dv; v(end,:)];
        clear e_ u_ v_ de du dv

        % 2. boundary conditions
        q = Q_in/100;
        % 2.1. west boundary (inflow)
        ff = find((yc>2450).*(yc<2550));
        for j = ff
            c_s = Equ3Iter(2.0, -uxR(j,1)-2*sqrt(grav*hxR(j,1)), 0, grav*q, ...
                           sqrt(grav*hxR(j,1)));
            h_s = c_s.^2/grav;      u_s = q/h_s;
            hxL(j,1) = h_s;         uxL(j,1) = u_s;
            exL(j,1) = h_s + 0.5*(zbp(j,1)+zbp(j+1,1));
            vxL(j,1) = 0.0;
        end
        % 2.2. east boundary (outflow)
        ff = find((yc>1450).*(yc<1550));
        for j = ff
            h_s = eta_out - 0.5*(zbp(j,end)+zbp(j+1,end));
            u_s = uxL(j,end) + 2*sqrt(grav*hxL(j,end)) - 2*sqrt(grav*h_s);
            hxR(j,end) = h_s;         uxR(j,end) = u_s;
            exR(j,end) = h_s + 0.5*(zbp(j,end)+zbp(j+1,end));
            vxR(j,end) = 0.0;
        end
        % 2.3. south boundary (inflow)
        ff = find((xc>1950).*(xc<2050));
        for i = ff
            c_s = Equ3Iter(2.0, -vyR(1,i)-2*sqrt(grav*hyR(1,i)), 0, grav*q, ...
                           sqrt(grav*hyR(1,i)));
            h_s = c_s.^2/grav;      u_s = q/h_s;
            hyL(1,i) = h_s;         vyL(1,i) = u_s;
            eyL(1,i) = h_s + 0.5*(zbp(1,i)+zbp(1,i+1));
            uyL(1,i) = 0.0;
        end
        % 2.4. north boundary (inflow)
        ff = find((xc>3950).*(xc<4050));
        for i = ff
            c_s = Equ3Iter(2.0, -vyL(end,i)-2*sqrt(grav*hyL(end,i)), 0, -grav*q, ...
                           sqrt(grav*hyL(end,i)));
            h_s = c_s.^2/grav;      u_s = q/h_s;
            hyR(end,i) = h_s;     	vyR(end,i) = -u_s;
            eyR(end,i) = h_s + 0.5*(zbp(end,i)+zbp(end,i+1));
            uyR(end,i) = 0.0;
        end

        clear u_s h_s ff j i
        % 3. flux terms (F and G)
        F1L = hxL.*uxL;
        F2L = hxL.*uxL.*uxL + 0.5*grav*(exL.*exL - ...
              exL.*(zbp(1:end-1,:)+zbp(2:end,:)));
        F3L = hxL.*uxL.*vxL;
        F1R = hxR.*uxR;
        F2R = hxR.*uxR.*uxR + 0.5*grav*(exR.*exR - ...
              exR.*(zbp(1:end-1,:)+zbp(2:end,:)));
        F3R = hxR.*uxR.*vxR;

        G1L = hyL.*vyL;
        G2L = hyL.*uyL.*vyL;
        G3L = hyL.*vyL.*vyL + 0.5*grav*(eyL.*eyL - ...
              eyL.*(zbp(:,1:end-1)+zbp(:,2:end)));
        G1R = hyR.*vyR;
        G2R = hyR.*uyR.*vyR;
        G3R = hyR.*vyR.*vyR + 0.5*grav*(eyR.*eyR - ...
              eyR.*(zbp(:,1:end-1)+zbp(:,2:end)));

        % 4. calculate the flux by HLL
        [sxL sxR] = WaveSpeed(hxL, hxR, uxL, uxR);
        F1 = HLLSolver(F1L, F1R, sxL,sxR, exL,exR);
        F2 = HLLSolver(F2L, F2R, sxL,sxR, hxL.*uxL,hxR.*uxR);
        F3 = HLLSolver(F3L, F3R, sxL,sxR, hxL.*vxL,hxR.*vxR);
        [syL syR] = WaveSpeed(hyL, hyR, vyL, vyR);
        G1 = HLLSolver(G1L, G1R, syL,syR, eyL,eyR);
        G2 = HLLSolver(G2L, G2R, syL,syR, hyL.*uyL,hyR.*uyR);
        G3 = HLLSolver(G3L, G3R, syL,syR, hyL.*vyL,hyR.*vyR);
        clear sxL sxR syL syR F1L F1R F2L F2R F3L F3R G1L G1R G2L G2R G3L G3R
        % 4.1. west boundary
        F1(:,1) = 0;        F3(:,1) = 0;
        F2(:,1) = 0.5*grav*(exR(:,1).^2 - exR(:,1).*(zbp(1:end-1,1)+zbp(2:end,1)));
        %      inflow
        ff = find((yc>2450).*(yc<2550));
        F1(ff,1) = hxL(ff,1).*uxL(ff,1);
        F2(ff,1) = F2(ff,1) + hxL(ff,1).*uxL(ff,1).*uxL(ff,1);
        F3(ff,1) = hxL(ff,1).*uxL(ff,1).*vxL(ff,1);
        % 4.2. east boundary
        F1(:,end) = 0;   	F3(:,end) = 0;
        F2(:,end) = 0.5*grav*(exL(:,end).^2 - exL(:,end).*(zbp(1:end-1,end)+zbp(2:end,end)));
        %      outflow
        ff = find((yc>1450).*(yc<1550));
        F1(ff,end) = hxR(ff,end).*uxR(ff,end);
        F2(ff,end) = F2(ff,end) + hxR(ff,end).*uxR(ff,end).*uxR(ff,end);
        F3(ff,end) = hxR(ff,end).*uxR(ff,end).*vxR(ff,end);
        % 4.3. south boundary
        G1(1,:) = 0;        G2(1,:) = 0;
        G3(1,:) = 0.5*grav*(eyR(1,:).^2 - eyR(1,:).*(zbp(1,1:end-1)+zbp(1,2:end)));
        %      inflow
        ff = find((xc>1950).*(xc<2050));
        G1(1,ff) = hyL(1,ff).*vyL(1,ff);
        G2(1,ff) = hyL(1,ff).*uyL(1,ff).*vyL(1,ff);
        G3(1,ff) = G3(1,ff) + hyL(1,ff).*vyL(1,ff).*vyL(1,ff);
        % 4.4. north boundary
        G1(end,:) = 0;      G2(end,:) = 0;
        G3(end,:) = 0.5*grav*(eyL(end,:).^2 - eyL(end,:).*(zbp(end,1:end-1)+zbp(end,2:end)));
        %      inflow
        ff = find((xc>3950).*(xc<4050));
	    G1(end,ff) = hyR(end,ff).*vyR(end,ff);
        G2(end,ff) = hyR(end,ff).*uyR(end,ff).*vyR(end,ff);
        G3(end,ff) = G3(end,ff) + hyR(end,ff).*vyR(end,ff).*vyR(end,ff);
        
        clear ff exL exR eyL eyR hxL hxR hyL hyR uxL uxR uyL uyR vxL vxR vyL vyR
        % 5. source terms
        Cf = grav * n.^2 .* h.^(-1/3);
        tau_x = rho*Cf.* u .*sqrt(u.*u + v.*v);
        tau_y = rho*Cf.* v .*sqrt(u.*u + v.*v);
        S1 = zeros(Ny,Nx);
        S2 = -tau_x/rho - grav*eta.*zbx;
        S3 = -tau_y/rho - grav*eta.*zby;

        % 6. time step
        % 6.1 solve eta
        eta = eta - dt/dx*(F1(:,2:end)-F1(:,1:end-1)) ...
                  - dt/dy*(G1(2:end,:)-G1(1:end-1,:)) + dt*S1;
        % 6.2 solve h*u
        hu = h.*u - dt/dx*(F2(:,2:end)-F2(:,1:end-1)) ...
                  - dt/dy*(G2(2:end,:)-G2(1:end-1,:)) + dt*S2;
        % 6.3 solve h*v
        hv = h.*v - dt/dx*(F3(:,2:end)-F3(:,1:end-1)) ...
                  - dt/dy*(G3(2:end,:)-G3(1:end-1,:)) + dt*S3;

        h = eta - zbc;
        u = hu./h;
        v = hv./h;
        clear hu hv k
    end
    
    t = t+dt;
    eta = 0.5*(eta + etan);
    h = eta - zbc;
    u = 0.5*(u + un);
    v = 0.5*(v + vn);
    clear etan hn un vn
    
    % 7. plot
    disp(['T = ' num2str(t)  's now.']);
    if (t >= plot_int*tplot)
        figure(1)
        set(gcf,'position',[962,42,958,953]);
        subplot(2,1,1)
        axis([0 Lx 0 Ly])
        pcolor(Xc, Yc, eta), shading interp, colormap jet, colorbar, hold on
        % quiver(Xc, Yc, u, v, 'w')
        title(['Water Level (m) @ T = ' num2str(t)  's'])
        set(gca,'FontName','Times New Roman','FontSize',14)

        subplot(2,1,2)
        axis([0 Lx 0 Ly])
        pcolor(Xc, Yc, sqrt(u.*u+v.*v)), shading interp, colormap jet, colorbar, hold on
        quiver(Xc, Yc, u, v, 'w')
        title(['Velocity (m/s) @ T = ' num2str(t)  's'])
        set(gca,'FontName','Times New Roman','FontSize',14)
        tplot = tplot + 1;
    end
end

5. 其余子函数：包括minmod限制器、HLL求解器、一元三次方程求解器Equ3Iter等。

结果展示

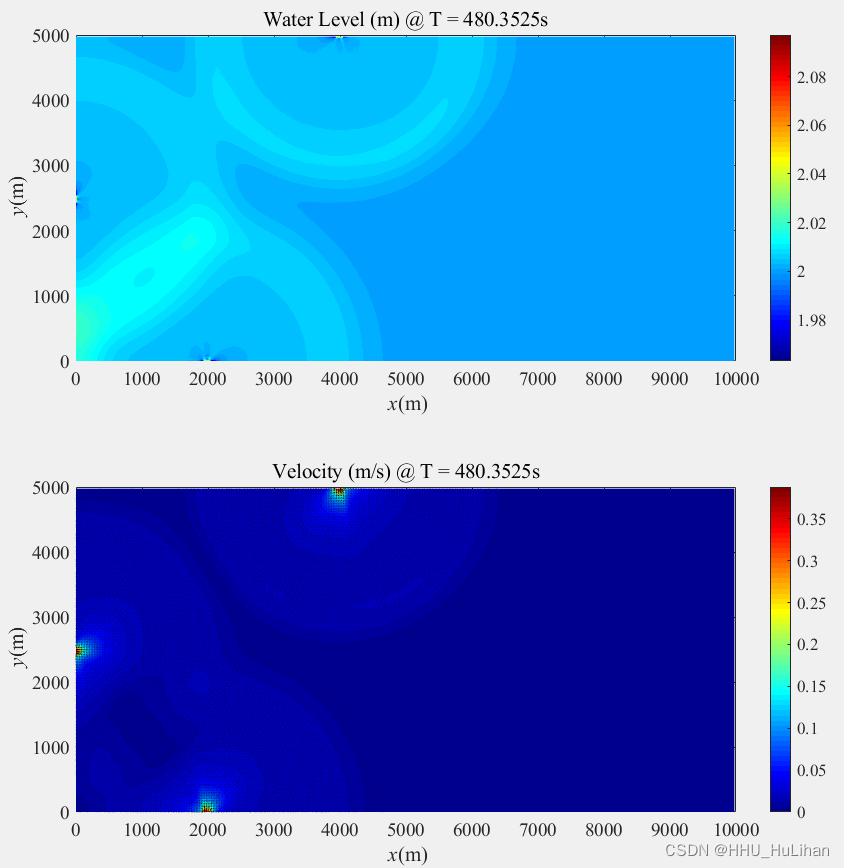
写在最后

1. 这个代码可以运行，但是总体上计算的并不快。我不知道是不是matlab编译器本身的原因。如果有用别的代码进行尝试的朋友，可以留言说说你们的计算速度如何。
2. 实际的入流边界条件远比我考虑的复杂，首先要考虑是临界流还是亚临界流，而本模型默认用亚临界流的入流条件；其次，我将入流边界处的流速设定为均匀分布的，这不一定符合实际，可能用下列公式更好。

流量边界条件：
对于这m条边界上的总流量$Q$，某一网格$i$边上的单宽流量$q_i$是：
$$q_i=\frac{L_i^{\prime }{h}_i^{1.5}{C}_i}{{\sum }_{k=1}^m{L}_k^{\prime }{h}_k^{1.5}{C}_k}Q$$
式中，$L^{\prime }$表示流量边界对应网格边的边长，$h$表示对应网格的水深，$C$表示对应网格的摩阻力项，有$C=\frac{h^{1/6}}{n}$，n为曼宁系数。之后根据求出的单宽流量，依次处理每个边界网格的通量值。

---

1. Liang Q , Marche F .Numerical resolution of well-balanced shallow water equations with complex source terms[J].Advances in Water Resources, 2009, 32(6):873-884.DOI:10.1016/j.advwatres.2009.02.010. ↩︎