依据工况数据计算整车驱动力
任务要求:给一段行驶工况(车速随时间的曲线)和整车参数求解驱动力。分别用matlab脚本语言和simulink实现并绘制曲线。
一、理论介绍
首先学习一下理论部分,以下是汽车在上坡时车辆受力示意图,是空气阻力,是前轮滚动力矩,是后轮滚动力矩。
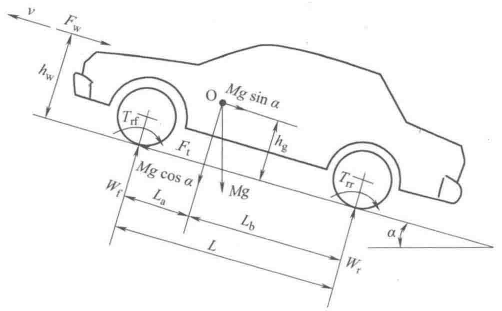
F t = ∑ F F_t=\sum{F} Ft=∑F(1)
驱动力等于阻力之和。
阻力分为滚动阻力、空气阻力、加速阻力和坡道阻力。
滚动阻力是由轮胎材料迟滞作用造成,具体可参考汽车理论内容。计算公式为:
F f = G F f c o s ( α ) F_f=GF_fcos(\alpha) Ff=GFfcos(α)(2)
该公式类似高中摩擦阻力,可以这样记忆,但不可这样理解!
空气阻力计算公式:
F w = C D A u a 2 ( α ) 21.15 F_w=\frac{C_DAu_a^2(\alpha)}{21.15} Fw=21.15CDAua2(α)(3)
C D C_D CD—空气阻力系数;A—迎风面积( m 2 m^2 m2); U a U_a Ua—车速(km/h)。
加速阻力:
F a = δ m d u d t F_a=\delta m\frac{du}{dt} Fa=δmdtdu(4)
δ \delta δ是旋转质量换算系数,1.0-1.5之间。
坡道阻力(重力在坡道上分力):
F t = G s i n ( α ) F_t=G sin(\alpha) Ft=Gsin(α)(5)
驱动力为:
F f = G F f c o s ( α ) + C D A u a 2 ( α ) 21.15 + δ m d u d t + G s i n ( α ) F_f=GF_fcos(\alpha)+\frac{C_DAu_a^2(\alpha)}{21.15}+\delta m\frac{du}{dt}+G sin(\alpha) Ff=GFfcos(α)+21.15CDAua2(α)+δmdtdu+Gsin(α)(6)
二、软件介绍
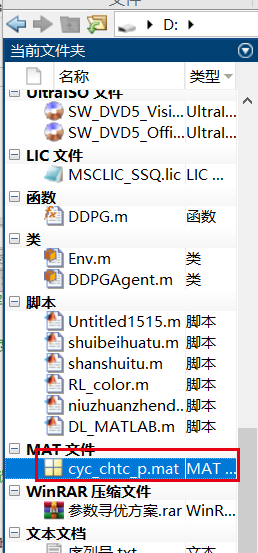
使用matlab2021a进行案例教学。Matlab打开一般有以下几个部分①脚本编辑窗口 ②命令行窗口 ③工作区 ④当前文件夹,其它两个看截图文字吧。工作区相当于内存,程序或者simulink运行时调用参数来自这里。当前文件夹的东西相当于电脑硬盘存储的东西。如果想改变界面布局可点击“主页→布局”进行修改。

什么是脚本:在格式上没有严格输入输出的程序。
什么是Simulink:图形化建模仿真工具。
三、脚本实现
程序要多写注释,方便日后理解与修改。思考程序完成的功能后,把要解决的步骤都写进注释。

Matlab中在=右边是需要定义的,等号左边的量可以不用定义。
在命令行中敲入
a=1;
b=a*2

发现命令行显示b=2,但没显示a
再换一种方式
a=1
b=a*2;

这次显示了b却没有显示a。说明在命令末尾加分号(“;”)可以不在命令行中显示该变量数值。
这个了解后,看公式(2),把滚动阻力公式用代码表示出来。在matlab中cos计算,直接用cos()函数即可。

保存代码,会让你存为文件,存了后点击运行。

在命令行窗口显示的黑色字为保存的文件名,红色字为报错信息,原来是公式中的veh_mass没定义。我们到图中标红的地方定义参数。

当前应该写为下图形式,运行。这里说明下, .*表示点乘,一个数点乘以数组或者矩阵,等价于这个数和数组里的每一个数都相乘。*如果用在矩阵中代表矩阵的乘法,是有严格的维数要求,可以参考线性代数。

运行后没有报错,查看工作区变量。计算的滚动阻力为104.1822N。

滚动阻力和加速阻力都和速度有关,因此需要导入速度。速度是随时间变化的,因此他是一个二维数组,第一列为时间,第二列为速度。

加载的mat文件必须在matlab当前工作文件夹里。
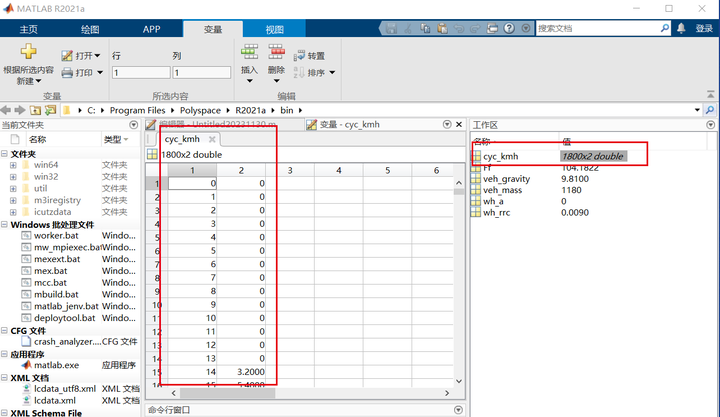
导入后在工作空间找加载出来的变量cyc_kmh,鼠标双击该变量可以看到在编辑窗口显示了变量,是一个2列1800行的数组,第一列为时间,第二列为车速。
现在来计算空气阻力,看公式发现需要定义CD值,迎风面积A,速度就是加载出来的cyc_kmh。


CD和A是系数,速度Ua是随时间变化的量。其中cyc_kmh(:,2)表示取了cyc_kmh中的第二列的数。逗号前表示行,逗号后表示列。“:”表示这一行或者这一列都取。
空气阻力也应该和cyc_kmh一样,第一列为时间,第二列为每一时刻的空气阻力。
定义下,可以直接让控制阻力的值等于cyc_kmh,然后将第二列重新赋值。
到这里我们想看一下空气阻力算的对不对,可以用matlab界面的画图功能将曲线画出来。
双击变量Fw,选中第二列(选的时候点第二列的数字2),点击绘图,点击plot。



这个时候会出现图窗,Figure 1,这样画图默认的横轴是从1、2、3,纵轴对应我们选中的数值。如果横轴数据要严格和第一列对应。用代码会比较好实现。


计算加速阻力,要先求出加速度。求加速度需要对速度进行微分,我们的速度是1s一个数据(采样频率为1Hz)。简单的方法是采用(下一时刻速度-当前时刻速度)/时间间隔(1s)。怎么实现呢?
可以用循环,matlab差分函数diff或者数组实现。为了让大家明白数组计算的好处,我这里用数组的方式实现,这是也是matlab的优势。matlab是矩阵实验室英文单词的缩写
在以后能用循环计算的地方,想一想能否用我这里提到的数组的方法实现。

veh_v_表示下一时刻速度,在cyc_kmh第二列数据,把第一个去掉,后面的往前挪。为了让维数一致,在最后补了个0。可以看到这种做法比循环简单多了。
[ ]里可以是具体的数如[1 2 3],表示一个1行3列的数组。[1;2;3]表示3行1列的数据。cyc_kmh(2:end,2)表示取第二列从第二个数到最后一个,其维数是1799行1列。如果在后面加0,就应该在列的方向上加。所以用分号“;”。
我们暂且取旋转质量换算系数为1。代码为

计算驱动力和绘制曲线在上述步骤中讲述过相关方法直接上最终的代码
`%程序要多写注释,方便日后理解与修改
%%定义参数
clear
veh_gravity=9.81; %重力加速度
veh_mass=1180;%整车最大质量 kg
wh_rrc=0.012;%滚动阻力系统
wh_a=0;%坡道
veh_CD=0.335;%CD值
veh_FA=2;%m^2
%%导入行驶工况
load(‘cyc_chtc_p.mat’)%加载工况数据,中国工况
%第一列为时间,第二列为车速,km/h
%%计算滚动阻力
Ff=cyc_kmh;
Ff(:,2)=veh_mass.*veh_gravity.*wh_rrc.*cos(wh_a);
%%计算空气阻力
Fw=cyc_kmh;%定义Fw
Fw(:,2)=veh_CD.*veh_FA.*cyc_kmh(:,2).^2/21.15;%给Fw赋值
%%计算加速阻力
veh_a=cyc_kmh;%定义veh_a 车辆加速度
veh_v_=[cyc_kmh(2:end,2);0];%
veh_v=cyc_kmh(:,2);
veh_a(:,2)=(veh_v_-veh_v)./1./3.6;%加速度单位为m^2
Fa=cyc_kmh;
Fa(:,2)=veh_mass.*veh_a(:,2);
%%计算坡道阻力
Fg=cyc_kmh;
Fg(:,2)=veh_mass.*veh_gravity.*sin(wh_a);%由于坡度是0,这里计算出来应该是0
%%计算驱动力
Ft=cyc_kmh;
Ft(:,2)=Ff(:,2)+Fw(:,2)+Fa(:,2);
%%绘制结果曲线
figure
plot(Ff(:,1),Ff(:,2))
figure
plot(Fw(:,1),Fw(:,2))
figure
plot(Fa(:,1),Fa(:,2))
figure
plot(Ft(:,1),Ft(:,2))`
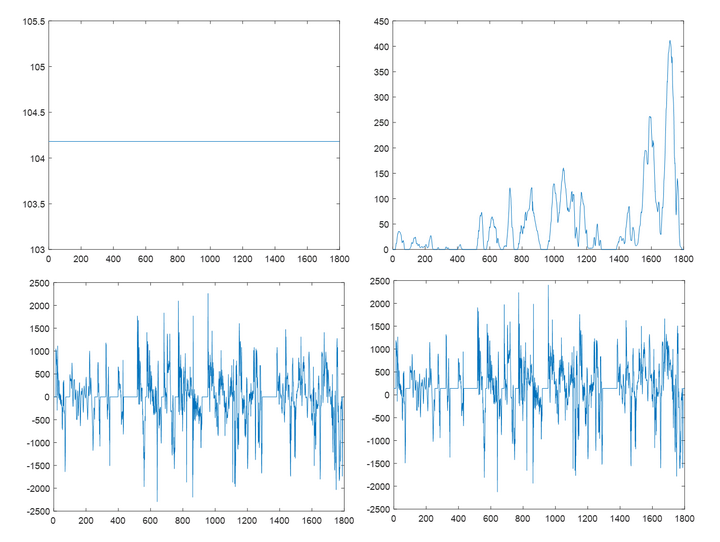
最终结果
计算滚动阻力时有一个bug,不过不影响咱们学matlab。
代码所需的mat文件。mat文件是matlab用来存储数据的。
链接:https://pan.baidu.com/s/1fCvWrzZkLvCh5TK7jZA9BQ
提取码:a61a
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








