GPS 入门 11——GPS C/A码产生与性质

• C/A码产生方法

根据GPS ICD描述，CA码发射发生器使用2个M序列构成，分别被称为G1序列和G2序列。每个卫星测距码信号使用的唯一C/A码序列就是通过将G1序列和一定抽头选择后的G2序列模2和(modulo-2 sum,其实就是异或运算(^,xor())，就是二进制加法)产生的。

每个M序列寄存器都是10Bit，则根据M序列性质，G1序列和G2序列的周期都是2^10-1=1023。两个序列模2和运算得到的Gold码周期也是1023，也就是书上到处说的1023个码片(CA Chip)。

由于Gold码周期是1023个码片，所以在1.023MHz时钟驱动下，一个周期信号长度(1023个码片)为1ms，即每隔1ms产生一个周期的全部1023个码片，每个码片持续时间长度为1ms/1023 ≈1us.

如下图是2个线性移位寄存器组，每个寄存器组是10bit，上本部分产生G1序列，下半部分产生G2序列，受GPS时钟控制。CA码时钟是1.023MHz。

输出的C/A码是G1的最后一级寄存器内容和G2抽头选择寄存器输出，进行模2和运算输出。

GPS CA码通过抽头选择器方式产生

M序列的使用一般都是提供一个多项式，说明抽头控制；

G1和G2生成多项式

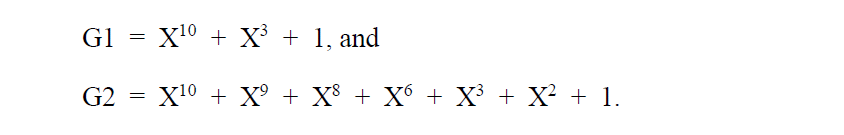
G1和G2的初始相位设置为全1.M寄存器初始值不能全0，否则反馈值即根据以上多项式计算出来的数值永远是0，得到的M序列也是全0.

• M序列多项式如何使用呢？

如G1多项式，到底是如何进行运算的呢？X代表什么呢？其实就是二进制加法运算。X^10就是把第10级寄存器数据位数据取出来，X^3就是把第3级寄存器数据取出来。这个寄存器索引从1开始，1-10进行编号，1是常数，模2运算是必须加入运算的。如下图，从3抽头和10抽头读取数据，运算后，送到输入端。

G1序列发生控制详细图

实际运算是，就是M序列寄存器位的数据与M多项式按位相乘，然后模2累加各个对应位乘法结果，M多项式为表示出来的各个为按0系数处理。M多项式就是对寄存器各个位进行加权累加和而已，只是这个权值是0或者1，累加是按照模2累加。

这个M多项式称为特征多项式。式中x仅指明其系数gi的值（1或0），x本身的取值并无实际意义，也不需要去计算x的值。例如，若特征方程为f(x)=1+x+x4则它仅表示x0,x1和x4的系数c0=c1=c4=1,其余为零。经严格证明：若反馈移位寄存器的特征多项式为本原多项式，则移位寄存器能产生m序列。只要找到本原多项式，就可构成m系列发生器。

MATLAB内实现一般按照如下方法：

% G1 LFSR: x^10+x^3+1

s = [0 0 1 0 0 0 0 0 0 1]; %选择tap3 和tap10

g1 = ones(1,n); %initialization vector for G1

.....

g1 = [ mod( sum(g1.*s) , 2 ) g1(1:n-1) ]; %该语句循环往复即可得到G1序列，

程序内，模2和运算即： mod( sum(g1.*s) , 2 ) ，乘累加 sum(g1.*s)然后模2运算。

一般这样运算出来的结果是0或1，而我们MATLAB内仿真模2乘法时，都是把0转换为-1运算。这样模2和运算直接转换为乘法运算 。

CA码一段波形如下：

• C/A码自相关和互相关

C/A码为周期序列信号，重复周期为1023位或1ms，对于C/A码序列本身，具有良好的自相关性。

即在在同一C/A码序列中任意截取两长度都为1023位的序列，如果两个序列完全一样，则产生最大的相关值，否则，相关值几乎为0。

两个序列分别用一个向量表示，其自相关值即为两个向量对应值乘积的和，假设用C(i)、C(i+i0) ,i=1,...,1023 ,i0为一个整数，　即第二个向量相对与第一个向量有一个偏差i0，超前或朝后，这样他们的自相关函数的值为（序列按1、－1计）

C/A码相关运算公式

以上公式意思就是将C/A码延迟一段时间i0之后，和自身乘积、累加、平均。因为C/A码是周期函数，则Rii也是周期函数，周期是1023，和C/A码周期一致。

当

, 即两个序列码相位不同，

当

, 即两个序列码相位相同，

下图是序列自相关图：

CA码具有周期性，下图是CA码自相关函数周期性显示，可见，周期就是CA码的周期1023.

同样，如果在不同C/A码序列中任意截取两长度都为1023位的序列，则无论两序列码相位是否相同与否，其相关值都很小。分别表示两个不同C/A 码的码序列。其中,i=1,1023 ,i0为一个整数，即第二个向量相对与第一个向量有一个偏差i0，超前或朝后，这样他们的互相关函数的值为（序列按1、－1计），对于所有i0有[1]，

即不同C/A 码之间几乎不存在相关性.

下图是两个CA码互相关图。可见，互相关只有3个数值：{-1,-65,63}

相关函数和功率谱是一对FFT变换对。

下图是CA码相关函数的FFT变换，可见到CA码带宽是2M左右

自相关函数近似一个冲击函数，由于冲击函数的FFT谱近似为一个平坦的噪声频谱。CA码自相关函数和白噪声的自相关函数有点近似，但是CA码自相关函数其它位置数值不为0，与真正的白噪声又不一致：CA码自相关函数之周期函数，而白噪声的自相关函数则不是；延时为0时CA码自相关函数也无法使其它位置数值处处为0。所以CA码是伪随机，与真正的随机码类似但又不知真随机码。

CA码自相关函数两个相关值之间是线性变化，所以可以通过插值计算更加精确的CA码相位差，提高定位精度。

为啥互相关和自相关的FFT变换没啥差别呢？

参考资料：

GPS Acquisition and Tracking – C/A code spectrum (Part 1)​ blog.realspatiallabs.com/2018/05/28/gps-acquisition-and-tracking-c-a-code-spectrum/

GPS Acquisition and Tracking – C/A code spectrum (Part 2)​ blog.realspatiallabs.com/2018/05/28/gps-acquisition-and-tracking-c-a-code-spectrum-part-2/