集合论
主要内容
-
集合基本概念
- 属于、包含
- 幂集、空集
- 文氏图等
-
集合的基本运算
- 并、交、补、差等
-
集合恒等式
- 集合运算的算律,恒等式的证明方法
集合的基本概念
集合的定义
集合没有明确的数学定义
理解:由离散个体构成的整体称为集合,称这些个体为集合的元素
常见的数集:N,Z,Q,R,C等分别表示自然数,整数,有理数,实数,负数集合
集合表示法
枚举法–通过列出全体元素来表示集合
谓词表示法–通过谓词概括集合元素的性质
实例 枚举法自然数集合N={0,1,2,3…}
谓词法 S={x|x是实数 ,x^2-1=0}
元素和集合
- 集合的元素具有的性质
- 无序性:元素列出的顺序无关
- 相异性:集合的每个元素只计数一次
- 确定性:对任何元素和集合都能确定这个元素是否为该集合的元素
- 任意性:集合的元素也可以是集合
- 元素与集合的关系
- 隶属关系
- 集合的树形层次结构A={{a,b},{b},d}


集合与集合
集合与集合之间的关系
⊆
,
=
,
⊊
,
≠
,
⊂
\subseteq ,=,\subsetneq,\neq, \sub
⊆,=,⊊,=,⊂
定义6.1 幂集
实例 计数,如果|A|=n,则 幂集的个数为2^n
全集E:包含了所有集合的集合 全集具有相对性,与问题有关,不存在绝对的全集
以下描述的集合是什么?(U表示论域)
集合的运算
初级运算
集合的基本运算有 并
相对补 A-B ={x|}
对称差 (A-B)∪(B-A)
绝对补集
并和交运算可以推广到有穷个集合上,即

广义运算
集合的广义并与广义交
广义并
文氏图
求1到100之间(包含 1和1000在内)即不能被5 和 6 整除,也不能被8整除的数有多少个?
定义以下集合
1.能够被5整除的数 200个
能够被6整除的数 166个
能够被8整除的数 125个
按照荣次原理,需要将能够被 5和6 ,5和8 6和8 同时整除的数减去,在加上同时能够被5 6 8整除的数,具体计算可参考下面的公式
不被5 6 8整除的数 = 总数-(能够被5整除的数+能够被6整除的数+能够被 8整除的数) -
容斥原理
- 容斥原理是组合数学中的一个重要原理,他在技术问题中占有很重要的地位
- 容斥原理所研究的问题是与若干有限集的交、并、或差有关的计数
- 在实际工作中,有时需要计算某种性质的元素个数

求不超过20的正整数中2或3的倍数的个数
2的倍数
对于求两个有限集合A和B的并集的元素数目
定理1 |A∪B|=|A|+|B|-|A∩B|
即具有性质A或B的元素的个数 等于具有性质A的元素个数和具有兴致B的元素个数的和,减去同时具有性质A和B的元素个数
计算1到700之间能被7整除的整数个数
直接计算相当麻烦,间接计算非常容易
先计算1到700之间能够被7整除的整数个数700/7=100
所以1到700之间不能被7整除的整数个数 700-100=600
逆向思维方式
一个学校只有三门课程:数学、物理、化学。已知修这三门课的学生分别有170、130、120人,同时修数学、物理的学生45人,同时修数学、化学的20人;同时修物理、化学22人,同时修三门课的三人,假设每个学生至少修一门课,问这学校共有多少学生?
令A、B、C分别为修数学、物理、化学的学生集合
|A∪B∪C|
=|A|+|B|+|C|-|A∩B|-|B∩C|-|C∩A|+|A∩B∩C|
=170+130+120-45-22-20+3=336
即学校共有336名学生
对于一般的n个有限集合
错位排列问题
在一个餐厅里,新雇员寄存了N个人的帽子,忘记把寄存号放在帽子上。当顾客取回他们的帽子时,这个雇员从剩下的帽子中随机选择发给他们。问没有一个人收到自己帽子的概率
这本质上就是一个错排问题。
当n=1时,{1}的全排列只有一个(1),他不是错位 所以D1=0
当n=2时,{1,2}的全排列有两个(1,2) 和(2,1)
前者不是错位,后者是错位,所以D2=1
当n=3时,{1,2,3}的全排列有6个
{1,2,3}{1,3,2}{3,2,1}{2,1,3},{3,1,2}{2,3,1}
前4个不是错位,后两个是错位 所以D3=2
全错位排列计数
n 个元素依次给以标号1,2…n N个元素的全排列中,求每个元素都不在自己原来位置上的排列数
设Ai为数i在第i位上的全体排列, i=1,2…n
注:总的排列数为n!
故总的错位排列数为

Ai在原来位置上,则Ai不能动,因而有
|Ai|=(n-1)! ,i=1,2…n
同理
|Ai∩Aj|=(n-2)!,i = 1,2,…,n i!=j
由于是错排,这些排列应排除
但是此时把同时有两个数不错排的排列多排除了一次,在补上时,把同时有三个数不错排的排列多补上了一次,应排除。。继续这一过程,得到错排的排列种数
每个元素都不在原来未知的排列数
例子:在8个字母ABCDEFGH的全排列中,求使得ACEG四个字母不在原来上的错排数目
8个字母的全排列中,令A1 A2 A3 A4 分别在ACEG在原来位置上的排列

二元关系
- 有序对与笛卡尔积
- 二元关系的定义与表示法
- 关系的运算
- 关系的性质
- 关系的闭包
- 等价关系与划分
- 偏序关系
有序对与笛卡尔积
定义7.1由两个元素x和y,按照一定的顺序组成的二元组称为有序对,记作<x,y>
有序对性质
- 有序性<x,y>不等<y,x>(当x不等y)
- <x,y>与<u,v>相等的充分必要条件是
<x,y>=<u,v> <=> x=u并且y=v
7.2
笛卡尔积
设A,B为集合,A与B的笛卡尔积记作AxB,且AxB={<x,y>|x∈A并且y属于B}
例子1
A={1,2,3} B={a,b,c}
AxB
={<1,a>,<1,b>,<1,c>,<2,a>,<2,b>,<2,c><3,a>,❤️,b>,❤️,c>}
BxA
={<a,1>,<b,1>,<c,1>,<a,2>,<b,2>,<c,2>,<a,3>,<b,3>,<c,3>}
A={∅} B={∅}
P(A)xA={<∅,∅>,<{∅},∅}
P(A)xB=∅
笛卡尔积的性质
不适合交换律
不适合结合律
对于并或交与运算满足分配律
若A或B有一个为空集,则AXB就是空集
二元关系
如果一个集合满足以下条件之一
集合非空,且他的元素都是有序对
集合是空集
则称该集合为一个二元关系,简称为关系,记作R
如果<x,y>∈R,可记作xRy,如果<x,y>不属于R,则记作 x y
实例 R={<1,2>,<a,b>}
S={<1,2>,a,b}
R是二元关系,当a,b不是有序对时,S不是二元关系
根据上面的写法,可以写1R2 aRb a c等
A到B的关系与A上的关系
定义7.4
设AB为集合,AXB的任何自己所定义的二元关系叫做A到B 的二元关系当A=B的时候叫做A上的二元关系
例三
A={0,1} B={1,2,3}那么
R1={0,2}R2=AXB R3=∅ R4={<0,1>}
R1,R2,R3,R4是从A到B的二元关系
R3和R4也是A上的二元关系
计数:|A|
|AxA|=n^2 AxA的自己有多少个 所以A上有2n2
例如A=3,则A上有 512个不同的二元关系
A上重要关系的实例
定义7.5设A为集合
空集 A上的关系,称为空关系
全域关系Ea={<x,y>|x∈A并且y∈A}=AXA
恒等关系Ia={<x,x>|x∈A}
小于等于关系Ia={<x,y>|x,y∈A并且x≤y}A为实数子集
整除关系 Da={<x,y>|x,y∈A并且x整除y}A为非0的整数子集
包含关系R属 ={<x,y>∈A并且x}A是集合族
例如A={1,2}则
EA={<1,1>,<1,2>,<2,1>,<2,2>}
IA={<1,1><2,2>}
例如A={1,2,3}B={a,b}
则lA={<1,1>,<1,2>,<1,3>,<2,2>,<2,3>,❤️,3>}
DA={<1,1>,<1,2>,<1,3>,<2,2>,❤️,3>}
A=P(B)={∅,{a},{b},{a,b}}则A上的包含关系
<∅,∅>,<∅,{a}>,<∅,{b}> <∅,{a,b}>,<{a},{a}>,<{a},{a,b}>
<{b},{b}>,<{b},{a,b}>,<{a,b}{a,b}>
关系的运算
关系的基本运算
关系的定义域、值域与域分别定义为
dom={x|存在y(<x,y>∈R)}
ranR={y|存在x(<x,y>∈R)}
fldR=domR∪ranR
例如R={<1,2>,<1,3>,<2,4>,<4,3>}
domR={1,2,4}
ranR={2,3,4}
fldR={1,2,3,4}
关系运算(逆与合成 )
关系的逆运算
R-1={<y,x>|<x,y>∈R}
关系的合成运算
FOG={<x,y>|存在t(<x,t>∈F∩<t,y>∈G)}
R={<1,2>,<2,3>,<1,4>,<2,2>}
S={<1,1>,<1,3>,<2,3>,❤️,2>,❤️,3>}
R-1={<2,1>,❤️,2>,<4,1>,<2,2>}
ROS={<1,3>,<2,2>,<2,3>}
SOR={<1,2>,<1,4>,❤️,3>,❤️,2>}
关系运算(限制与像)
设R是二元关系,A是集合
R在A上的限制记作R↾A 其中
R↾A={<x,y>|xRy并且x∈A}
A在R上的像记作R[A]其中,R[A]=ran(R↾A)
说明
R在A上的限制R↾A是R的子关系,及R↾A∈R
A在R上的像R[A]是ranR的子集,即R[A]属于ranR
例子R={<1,2>,<1,3>,<2,2>,<2,4>,❤️,2>}则
R={<1,2>,<1,3>,<2,2>,<2,4>,❤️,2>}则
R↾{1}={<1,2>,<1,3>}
R↾∅=∅
R↾{2,3}={<2,2>,<2,4>,❤️,2>}
R[{1}]={2,3}
R[∅]=∅
R[{3}]={2}
关系运算的性质
设F是任意的关系,则(F-1)-1=F
domF-1=ranF,ranF-1=domF
设F,G,H是任意的关系,则
(FoG)oH=Fo(GoH)
(FoG)-1=G-1 o F -1
关系的幂运算
设R为A上的关系,n为自然数,则R的n次幂定义为:
R0={<x,x>|x∈A}=IA
Rn+1=RnoR
注意
对于A上的任何关系R1和R2都有R10=R20=IA
对于A上的任何关系R都有R1=R
幂的求法
设A={a,b,c,d}R={<a,b>,<b,a>,<b,c>,<c,d>}
求R的各次幂,分别用矩阵和关系图表示
R与R^2的关系矩阵分别是
关系的性质
设R为A上的关系
若Vx(x∈A-><x,x>∈R),则称R在A上是自反的
若Vx(x∈A-><x,x>∉R),则称关系R在A上是反自反的
实例
自反:全域关系Ea 恒等关系Ia 小于等于关系LA,整除关系DA
反自反:实数集上的小于关系,幂集上的真包含关系‘
A={1,2,3} R1,R2,R3是A上的关系,其中
R1={<1,1>,<2,2>}
R2={<1,1><2,2>,❤️,3>,<1,2>}
R3={<1,3>}
R2自反 R3反自反 R1既不是自反的也不是反自反的
对称性与反对称
定义7.12设R为A上的关系
1.若VxVy(x,y∈A^<x,y>∈R-><y,x>∈R)则称R为A上对称的关系
若若VxVy(x,y∈A^<x,y>∈R-><y,x>∈R->x=y)则称R为A上的反对称关系
实例:对称关系A上的全域关系Ea 恒等关系IA 和空关系
反对称关系 恒等关系IA和空关系也是A上的反对称关系
设A={1,2,3} R1,R2,R3,R4都是A上的关系,其中
R1={<1,1>,<2,2>}
R2={<1,1><1,2>,<2,1>}
R3={<1,2>,<1,3>}
R4={<1,2>,<2,1>,<1,3>}
R1:对称和反对称
R2只有对称
R3:只有反对称
R4:不对称,不反对称
传递性
定义7.13设R为A上的关系,若
任意x任意y任意z(x,y,z属于A并且<x,y>属于R并且<y,z>∈R-><x,z>∈R)
则称R是A上的传递关系
实例:A上的全域关系EA,恒等关系IA和空关系∅,小于等于关系,整除关系,包含与真包含关系
设A={1,2,3}R1,R2,R3是A上的关系,其中
R1={<1,1>,<2,2>}
R2={<1,2>,<2,3>}
R3={<1,3>}
R1和R3是A上的传递关系,R2不是A上的传递关系
关系性质成立的充要条件
设R为A上的关系,则
- R在A上自反当且仅当IA是R的子集
- R在A上反自反当且仅当R∩IA=∅
- R在A上对称当且仅当R=R-1
- R在A上反对恒当且仅当R∩R-1是IA的子集
- R在A上传递当且仅当ROR是R的子集
关系性质的三种等价条件
| 自反性 | 反自反性 | 对称性 | 反对称性 | 传递性 | |
|---|---|---|---|---|---|
| 集合 | Ia是R的子集 | R∩IA=∅ | R=R-1 | R∩R-1是IA的子集 | ROR是MR的子集 |
| 关系矩阵 | 主对角线元素全是1 | 主对角元素全是0 | 矩阵是对称矩阵 | rij=1 **且i≠j*,** 则rji=0 | |
| 关系图 | 每个顶点都有环 | 每个顶点都没有环 | 两点之间有边,是一对方向相反的边 | 两点之间有边,是一条有向边 | 点xi到xj有边,到有边,则xi到也有到边j |
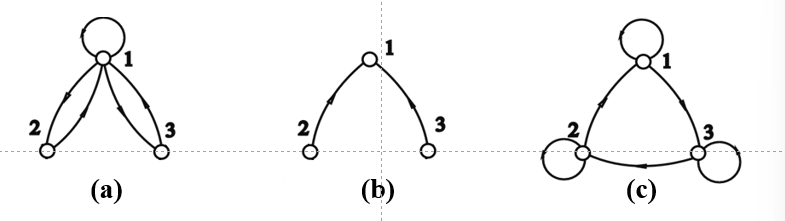
对称(两点之间有边,是一对方向相反的边)
反自反(每个顶点都没有环)、反对称(两点之间有边,是一条有向边)、传递
c自反, 反对称
关系的闭包
主要内容
- 闭包定义
- 闭包的构造方法
- 集合表示
- 矩阵表示
- 图表示
- 闭包的性质

一个对象

对象的圆闭包,橘黄色圈,满足
1,是圆的(性质)
2,包含所给对象
3,如果有个绿色圆也能包含该对象,就一定也能够包含这个橘黄圈
对象的正方形闭包,蓝色框,满足

1.是正方形的
2.包含所给对象
3.如果有个红色正方形也能包含该对象,就一定也能包含这个 青涩狂
闭包定义
定义7.4设R是非空集合A上的关系,R的自反(对称或传递)闭包是A上的关系R’,使得R’满足以下条件
- R‘是自反的(对称的或传递的)
- R是R’的子集
- 对A上任何包含R的自反(对称或传递)关系R’’ 有R’是R’’ R的自反闭包记作r®,对称闭包记作s®,传递闭包记作t®
定理7.10 设R为A上的关系,则有
- r®=R∪R0=R∪IA
- s®=R∪R-1
- t®=R∪R2∪R3…并RN
说明对有穷集A(|A|=n)上的关系,(3)中的并最多不超过Rn
**例子9 **
设A={a,b,c,d},R={<a,b>,<b,a>,<b,c>,<c,d>,<d,b>}
R和r®,s®,t®的关系图如下图所示

求传递闭包的算法
算法warshall
输入:M(R的关系矩阵)
输出:MT(t®的关系矩阵)
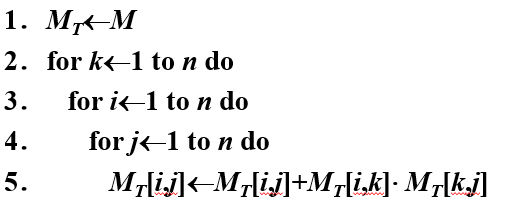
实例
设A={a,b,c,d}R={<a,b>,<b,a>,<b,c>,<c,d>,<d,b>}
R 的传递闭包的矩阵如下
M0
闭包的性质
定理7.11 设R是非空集合A上的关系则
(1)R是自反的当且仅当r®=R
(2)R是对称的当且仅当s®=R
(3)R是传递的,当且仅当t®=R
7.12设R1和R2是非空集合A上的关系,且R1是R2的子集,
则r(R1)是r(R2)子集,同理对于对称闭包与传递比表也是类似的
定理7.13设R是非空集合A上的关系
- 若R 是自反的,则s®与t®也是自反的
- 设R是对称的,r®与t®也是对称的
- 若R是传递的,则r®是传递的
证明,如果需要进行多个闭包运算,比如求R的自反,对称,传递的闭包tsr®运算顺序如下
tsr®=rts®=trs®
7.6等价关系与划分
- 等价关系的定义与实例
- 等价类及其性质
- 商集与集合的划分
- 等级关系与划分的一一对应
定义7.15设R是非空集合A上的关系,如果R是自反的,对称的和传递的,则称R为A上的等价关系,设R是一个等价关系,若<x,y>∈R,则称x等价于y。记作x~y
实例 A={1,2…8}如下定义A上的关系R
R={<x,y>|x,y∈A并且x与y模3 相等,即x除以3的余数与y除以3的余数相等,不难验证R为A上的等价关系,因为}
- 任意x∈A,有x=x(mod3)
- 任意x,y∈A,若x=y(mod3)则有y=x(mod3)
- 任意x,y,z∈A,若x=u(mod3),y=z(mod3),则有x=z(mod3)
模3等价关系的关系图

等价关系的关系矩阵与关系图
关系矩阵
- 主对角线元素等于1
- 对称矩阵
- MR=MRn
关系图
- 每一节点都有一自划线
- 如果有从a到b的弧,那么也有从b到a的弧
- 如果有从a到c有一条路径,则从a到c有一条弧
等价类定义
定义7.16设R 为非空集合A上的等价滚西,任意x∈A,令[x]R={y|y∈A交xRy}
称[x]R为x关于R的等价类,简称为x的等价类,简称为[x]
实例 A={1,2,,8}上模3等价关系的 等价类
[1]=[4]=[7]={1,4,7}
[2]=[5]=[8]={2,5,8}
[3]=[6]={3,6}
定理7.14设R是非空集合A上的等价关系,则
- 任意x∈A,[x]是A上的非空子集
- 任意x,y属于A,如果xRy,则[x]=[y]
- 任意x,y∈A,如果x
 y,则[x]与[y]不交
y,则[x]与[y]不交 - ∪{|x|x∈A}=A
商集与划分
定义7.14设R为非空集合A上的等价关系,以R的所有等价类作为元素的集合称为A关于R上的商集,记作A/R
A/R={[x]R|x∈A}
实例 设A={1,2,…8}A关于模3等价关系的 商集为
A/R={{1,4,7},{2,5,8},{3,6}}
A关于恒扥关系和全域关系的商集为
A/IA={{1},{2}…,{8}}
A/EA={{1,2,…,8}}
定义7.18设A为非空集合,若A的子集组π(π是P(A)的子集)满足
1.∅∉π
2.任意x任意y(x,y∈π交x≠y->x∩y=∅)
∪π=A
则称π是A的一个划分,称π中的元素为A的划分快
划分实例
设A={a,b,c,d}给定π1={{a,b,c},{d}}
π2={{a,b},{c},{d}}
π3={{a},{a,b,c,d}}
π4={{a,b},{c}}
π5={∅{,a,b},{c,d}}
π6={{a,{a}},{b,c,d}}
π1和π2是A的划分,其他都不是A的划分
实例
给出A={1,2,3}上所有的等价关系
解:先做出A的划分,从左到右分别记作π1,π2,π3,π4,π5

π1对应EA,π5对应IA,π2,π3和π4分别对应R2,R3,R4
R2={<2,3>,❤️,2>}∪IA
R3={<1,3>,❤️,1>}∪IA
R4={<1,2>,<2,1>}∪IA
偏序关系
主要内容
偏序关系
- 偏序关系的定义
- 偏序关系的实例
偏序集与哈斯图
偏序集中特殊元素及其性质
极大元、极小元、最大元、最小元、上界、下界、最小上届,最小下界
7.19偏序关系非空集合A上的自反,反对称和传递的关系
记作≤,设≤为偏序关系,如果<x,y>∈≤,则记作x≤y,读作x小于或等于 y
实例
集合A上的恒扥关系IA也是A上的偏序关系
小于或等于关系,整除关系和包含关系也是相应集合上的偏序关系
定义7.20设R为非空集合A上的偏序关系
- x,y∈A,x与y可比等价x≤y或y≤x
- 任取元素x和y,可能有以下几种情况发生 x<y 或 y<x x=y,x与y是不可比的
定义7.21R为非空集合的偏序关系
任意x,y∈A,x与y都是可比的,则称R为全序
实例:数集上的小于等于关系是全序关系,整除关系不是正整数集合上的全序关系
定义7.22x,y∈A,如果x<y且不存在z∈A使得x<z<y则称y覆盖x
例如{1,2,4,6}集合上整除关系,2覆盖1,4,和6,覆盖2,4不覆盖1
定义7.23集合A和A上的偏序关系≤一起叫做偏序集,记作<A,≤>
实例<Z,≤>,<P(A),R属于>
哈斯图:利用偏序关系的自反、反对称、传递性进行简化的关系图
特点
每个节点没有环
两个连通的节点之间的序关系通过节点位置的高低表示,位置低的元素的顺序在前
且 有覆盖关系的两个节点之间连边
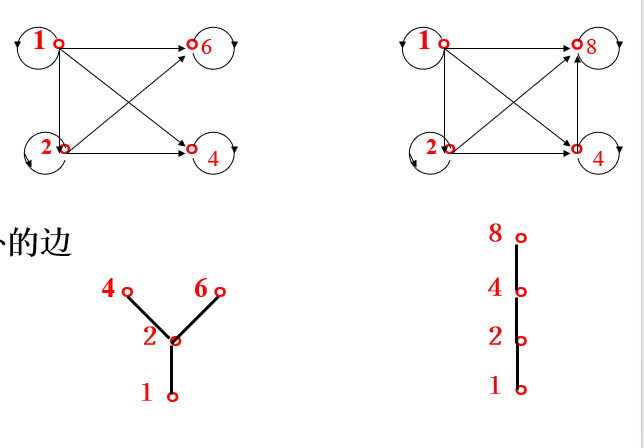
- 去环
- 去覆盖以外的边
- 重新排列
- 去剪头
例子
偏序集<{2,3,6,12,24,36},R整除>和<P({a,b,c}),R属于>的哈斯图
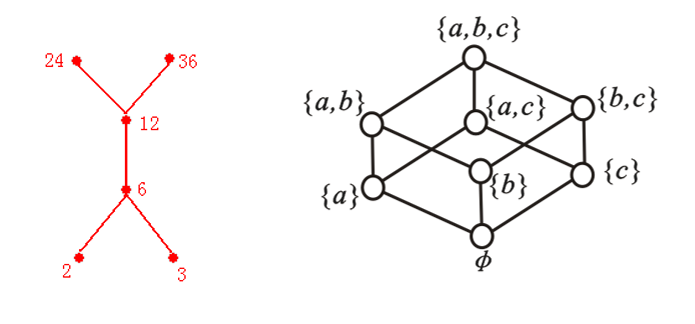
例子:已知偏序集<A,R>的哈斯图如下图所示,试求出集合A和关系R的表达式

偏序集中的特殊关系
定义7.24设<A,≤>为偏序集,B是A的子集,y∈B
- 若任意x(x∈B->y<=x)成立,则称y为B的最小元
- 若任意x(x∈B->y>=x)成立,则称y为B的最大元
- 若任意x(x∈B并且x<=y->x=y)成立,则称y为B的极小元
- 若任意x(x∈B并且y<=x->x=y)成立,则称y为B的极大元
性质
- 对于有穷集,极小元和极大元一定存在,可能存在多个
- 最小元和最大元不一定存在,如果存在一定唯一
- 最小元一定是极小元,最大元一定是极大元
- 孤立点即是极小元,也是极大元
偏序集中的特殊元素
- 若任意x(x∈B->x<=y)成立,则称y为B的上界
- 若任意x(x∈B->y<=x)成立,则称y为B 的下界
- 令C={y|y为B的上界},C的最小元为B的最小上界偶上确界
- 令D={y|y为B的下界},D的最大元为B的最大下界或下确界
性质
- 下界、上界、下确界、上确界不一定存在
- 下界、上界存在不一定唯一
- 下确界、上确界如果存在,则唯一
- 集合的最小元是其下确界,最大元是其上确界,反之不对
实例
设偏序集<A,≤>求A的极小元、最小元、极大元,最大元,设B={b,c,d}求B的下界,上界,下确界,上确界

解:
极小元:a,b,c,g
极大元:a,f,h
没有最小元和最大元
B的下界和最大下界都不存在
上界 d和f
最小上界为d
实例
某偏序关系的哈斯图如右图所示,讨论当B 取相应集合时,其最大元,最小元,极大元,极小元,上/下界,上/下确界

| B | 极小元 | 极大元 | 最小元 | 最大元 |
|---|---|---|---|---|
| {a,b} | a,b | a,b | 无 | 无 |
| {a,b,c} | a,b | c | 无 | c |
| {a,b,c,d} | a,b | c,d | 无 | 无 |
| {b,c,d,f} | b | f | b | f |
| {a,c,f,i} | a | i | a | i |
| B | 上界 | 下界 | 上确界 | 下确界 |
|---|---|---|---|---|
| {a,b} | c,d,e,f,g,h,i | 无 | 无 | 无 |
| {a,b,c} | c,e,f,h,i | 无 | c | 无 |
| {a,b,c,d} | f,h,i | 无 | f | 无 |
| {b,c,d,f} | f,h,i | b | f | n |
| {a,c,f,i} | i | a | i | a |
习题
设A={1,2,3}R={<x,y>|x,y∈A且x+2y<=6},S={<1,2>,<1,3>,<2,2>}
求R 的集合表达式
R-1
domR,ranR,fldR
ROS,R^3
r®,s®,t®
- R={<1,1>,<1,2>,<2,1>,<2,2>,❤️,1>}
- R-1={<1,1>,<2,1>,<1,2>,<2,2>,<1,3>}
- domR={1,2,3}ranR={1,2},fldR={1,2,3}
- RoS={<1,2>,<1,3>,<2,2>,<2,3>,❤️,2>,❤️,3>}
- R^3={<1,1>,<1,2>,<2,1>,<2,2>,❤️,1>,❤️,2>}
r®={<1,1>,<1,2>,<2,1>,<2,2>,❤️,1>,❤️,3>}
s®={<1,1>,<1,2>,<2,1>,<2,2>,❤️,1>,<1,3>}
t®={<1,1>,<1,2>,<2,1>,<2,2>,❤️,1>,❤️,2>}
设偏序集<A,R>的哈斯图如下所示
写出A和Rd的集合表达式
求该偏序集中的极大元,极小元,最大元,最小元

A={a,b,c,d,e}
R={<d,b>,<d,a>,<d,c>,<e,c>,<e,a>,<b,a>,<c,a>}并Ia
极大元和最大元是a
没有最小元

| B | 极小元 | 极大元 | 最小元 | 最大元 | 上界 | 上确界 | 下界 | 下确界 |
|---|---|---|---|---|---|---|---|---|
| {2,3} | 2,3 | 2,3 | 无 | 无 | 6,12,24,36 | 6 | 1 | 1 |
| {1,2,3} | 1 | 2,3 | 1 | 无 | 6,12,24,36 | 6 | 1 | 1 |
| {6,12,4} | 6 | 24 | 6 | 24 | 24 | 24 | 1,2,3,6 | 6 |
| A | 1 | 24,36 | 1 | 无 | 无 | 无 | 1 | 1 |
例题4
设R是Z上的模n等价关系,即x~y<=>x=y(modn)试给出由R确定的Z的划分π
设除以n余数为r的整数构成等价类[r],则[r]={kn+r|k∈z},r=0,1,…,n-1
π={[r]|r=0,1,…,n-1}
例题5
设R是A上的二元关系,设S={<a,b>|存在c(<a,c>∈R交<c,b>∈R)}证明如果RE是等价关系,则S也是等价关系
证:R是A上的等加固韩系







 文章介绍了集合论的基本概念,包括集合的定义、表示法和性质,如并、交、补等运算,以及集合间的包含关系。接着讨论了关系的类型,如自反、对称、传递性,并介绍了二元关系、幂运算、闭包以及等价关系和偏序关系的概念。此外,还提到了如何通过哈斯图来表示和分析偏序集。
文章介绍了集合论的基本概念,包括集合的定义、表示法和性质,如并、交、补等运算,以及集合间的包含关系。接着讨论了关系的类型,如自反、对称、传递性,并介绍了二元关系、幂运算、闭包以及等价关系和偏序关系的概念。此外,还提到了如何通过哈斯图来表示和分析偏序集。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








