1.引言
本文主要介绍以下三个方面的内容:
(1)Logistic Regression的基本原理,分布在第二章中;
(2)Logistic Regression的具体过程,包括:选取预测函数,求解Cost函数和J(θ),梯度下降法求J(θ)的最小值,以及递归下降过程的向量化(vectorization),分布在第三章中;
(3)对《机器学习实战》中给出的实现代码进行了分析,对阅读该书LogisticRegression部分遇到的疑惑进行了解释。没有基础的朋友在阅读该书的Logistic Regression部分时可能会觉得一头雾水,书中给出的代码很简单,但是怎么也跟书中介绍的理论联系不起来。也会有很多的疑问,比如:一般都是用梯度下降法求损失函数的最小值,为何这里用梯度上升法呢?书中说用梯度上升发,为何代码实现时没见到求梯度的代码呢?这些问题在第三章和第四章中都会得到解答。
(4)正则化项以及逻辑回归与别的模型的关系。
文中参考或引用内容的出处列在最后的“参考文献”中。文中所阐述的内容仅仅是我个人的理解,如有错误或疏漏,欢迎大家批评指正。下面进入正题。
2. 基本原理
Logistic Regression和Linear Regression的原理是相似的,按照我自己的理解,可以简单的描述为这样的过程:
(1)找一个合适的预测函数(Andrew Ng的公开课中称为hypothesis),一般表示为h函数,该函数就是我们需要找的分类函数,它用来预测输入数据的判断结果。这个过程时非常关键的,需要对数据有一定的了解或分析,知道或者猜测预测函数的“大概”形式,比如是线性函数还是非线性函数。
(2)构造一个Cost函数(损失函数),该函数表示预测的输出(h)与训练数据类别(y)之间的偏差,可以是二者之间的差(h-y)或者是其他的形式。综合考虑所有训练数据的“损失”,将Cost求和或者求平均,记为J(θ)函数,表示所有训练数据预测值与实际类别的偏差。
(3)显然,J(θ)函数的值越小表示预测函数越准确(即h函数越准确),所以这一步需要做的是找到J(θ)函数的最小值。找函数的最小值有不同的方法,Logistic Regression实现时有的是梯度下降法(Gradient Descent)。
3. 具体过程
3.1 构造预测函数
Logistic Regression虽然名字里带“回归”,但是它实际上是一种分类方法,用于两分类问题(即输出只有两种)。根据第二章中的步骤,需要先找到一个预测函数(h),显然,该函数的输出必须是两个值(分别代表两个类别),所以利用了Logistic函数(或称为Sigmoid函数),函数形式为:
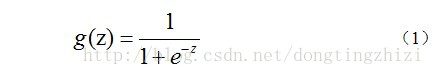
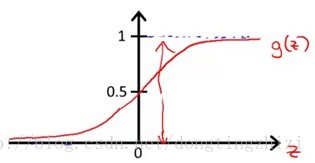
对应的函数图像是一个取值在0和1之间的S型曲线(图1)。
图1
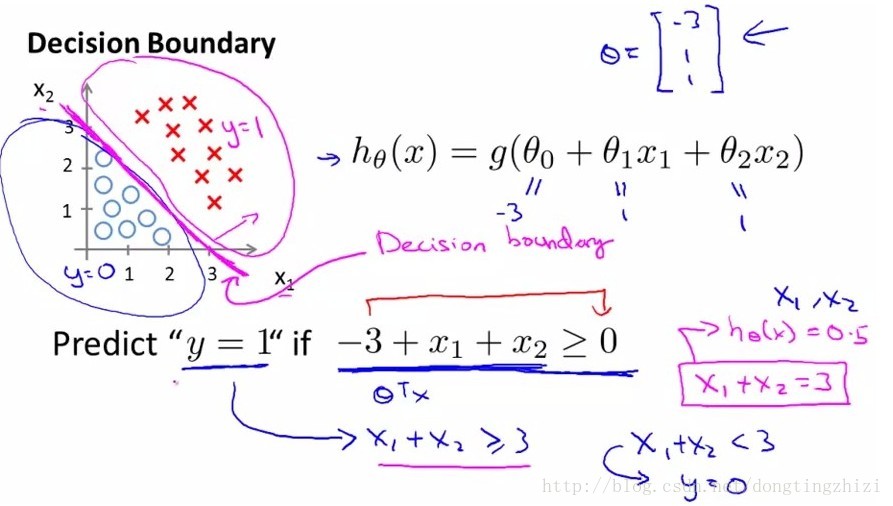
接下来需要确定数据划分的边界类型,对于图2和图3中的两种数据分布,显然图2需要一个线性的边界,而图3需要一个非线性的边界。接下来我们只讨论线性边界的情况。
图2
图3
对于线性边界的情况,边界形式如下:
构造预测函数为:
hθ(x)函数的值有特殊的含义,它表示结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为:
3.2 构造Cost函数
Andrew Ng在课程中直接给出了Cost函数及J(θ)函数如式(5)和(6),但是并没有给出具体的解释,只是说明了这个函数来衡量h函数预测的好坏是合理的。
实际上这里的Cost函数和J(θ)函数是基于最大似然估计推导得到的。下面详细说明推导的过程。(4)式综合起来可以写成:
取似然函数为:
对数似然函数为:
最大似然估计就是要求得使l(θ)取最大值时的θ,其实这里可以使用梯度上升法求解,求得的θ就是要求的最佳参数。但是,在Andrew Ng的课程中将J(θ)取为(6)式,即:
因为乘了一个负的系数-1/m,所以J(θ)取最小值时的θ为要求的最佳参数。
3.3 梯度下降法求J(θ)的最小值
求J(θ)的最小值可以使用梯度下降法,根据梯度下降法可得θ的更新过程:
式中为α学习步长,下面来求偏导:
上式求解过程中用到如下的公式:
因此,(11)式的更新过程可以写成:
因为式中α本来为一常量,所以1/m一般将省略,所以最终的θ更新过程为:
另外,补充一下,3.2节中提到求得l(θ)取最大值时的θ也是一样的,用梯度上升法求(9)式的最大值,可得:
观察上式发现跟(14)是一样的,所以,采用梯度上升发和梯度下降法是完全一样的,这也是《机器学习实战》中采用梯度上升法的原因。
3.4 梯度下降过程向量化
关于θ更新过程的vectorization,Andrew Ng的课程中只是一带而过,没有具体的讲解。
《机器学习实战》连Cost函数及求梯度等都没有说明,所以更不可能说明vectorization了。但是,其中给出的实现代码确是实现了vectorization的,图4所示代码的32行中weights(也就是θ)的更新只用了一行代码,直接通过矩阵或者向量计算更新,没有用for循环,说明确实实现了vectorization,具体代码下一章分析。
文献[3]中也提到了vectorization,但是也是比较粗略,很简单的给出vectorization的结果为:
且不论该更新公式正确与否,这里的Σ(...)是一个求和的过程,显然需要一个for语句循环m次,所以根本没有完全的实现vectorization,不像《机器学习实战》的代码中一条语句就可以完成θ的更新。
下面说明一下我理解《机器学习实战》中代码实现的vectorization过程。
约定训练数据的矩阵形式如下,x的每一行为一条训练样本,而每一列为不同的特称取值:
约定待求的参数θ的矩阵形式为:
先求x.θ并记为A:
求hθ(x)-y并记为E:
g(A)的参数A为一列向量,所以实现g函数时要支持列向量作为参数,并返回列向量。由上式可知hθ(x)-y可以由g(A)-y一次计算求得。
再来看一下(15)式的θ更新过程,当j=0时:
同样的可以写出θj,
综合起来就是:
综上所述,vectorization后θ更新的步骤如下:
(1)求A=x.θ;
(2)求E=g(A)-y;
(3)求θ:=θ-α.x'.E,x'表示矩阵x的转置。
也可以综合起来写成:
前面已经提到过:1/m是可以省略的。
4. 代码分析
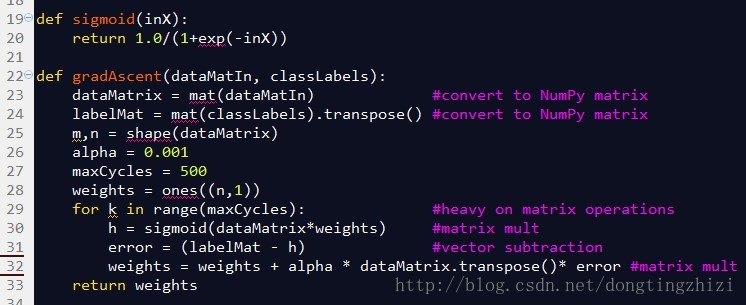
图4中是《机器学习实战》中给出的部分实现代码。
图4
sigmoid函数就是前文中的g(z)函数,参数inX可以是向量,因为程序中使用了Python的numpy。
gradAscent函数是梯度上升的实现函数,参数dataMatin和classLabels为训练数据,23和24行对训练数据做了处理,转换成numpy的矩阵类型,同时将横向量的classlabels转换成列向量labelMat,此时的dataMatrix和labelMat就是(18)式中的x和y。alpha为学习步长,maxCycles为迭代次数。weights为n维(等于x的列数)列向量,就是(19)式中的θ。
29行的for循环将更新θ的过程迭代maxCycles次,每循环一次更新一次。对比3.4节最后总结的向量化的θ更新步骤,30行相当于求了A=x.θ和g(A),31行相当于求了E=g(A)-y,32行相当于求θ:=θ-α.x'.E。所以这三行代码实际上与向量化的θ更新步骤是完全一致的。
总结一下,从上面代码分析可以看出,虽然只有十多行的代码,但是里面却隐含了太多的细节,如果没有相关基础确实是非常难以理解的。相信完整的阅读了本文,就应该没有问题了!^_^。
5.正则化
正则化不是只有逻辑回归存在,它是一个通用的算法和思想,所以会产生过拟合现象的算法都可以使用正则化来避免过拟合,在谈正则化之前先聊聊什么是过拟合。
5.1 过拟合
之前的模型介绍和算法求解可以通过训练数据集(图2中的三角形和星形)将分类模型训练好,从而可以预测一个新数据(例如图2中的粉色圆圈)的分类,这种对新数据进行预测的能力称为泛化能力。而对新数据预测的结果不好就是泛化能力差,一般来说泛化能力差都是由于发生了过拟合现象。过拟合现象是指对训练数据预测很好但是对未知数据预测不行的现象,通常都是因为模型过于复杂,或者训练数据太少。即当比值太大的情况下会发生过拟合。模型复杂体现在两个方面,一是参数过多,二是参数值过大。参数值过大会导致导数非常大,那么拟合的函数波动就会非常大,即下图所示,从左到右分别是欠拟合、拟合和过拟合。
在模型过于复杂的情况下,模型会学习到很多特征,从而导致可能把所有训练样本都拟合到,就像上图中一样,拟合的曲线将每一个点都正确的分类了。举个例子,假如要预测一个房子是贵还是便宜,房子的面积和所属的地区是有用的特征,但假如训练集中刚好所有贵的房子都是开发商A开发,便宜的都是开发商B开发,那么当模型变复杂能学习到的特征变多之后,房子是哪个开发商的会被模型认为是个有用特征,但是实际上这点不能成为判断的标准,这个现象就是过拟合。因此在这个例子中可以看到,解决的方法有两个,一个是减少学习的特征不让模型学到开发商的特征,一是增加训练集,让训练集有贵房子是B开发的样本。
从而,解决过拟合可以从两个方面入手,一是减少模型复杂度,一是增加训练集个数。而正则化就是减少模型复杂度的一个方法。
5.2 正则化的两种方法
由于模型的参数个数一般是由人为指定和调节的,所以正则化常常是用来限制模型参数值不要过大,也被称为惩罚项。一般是在目标函数(经验风险)中加上一个正则化项即
而这个正则化项一般会采用L1范数或者L2范数。其形式分别为。
首先针对L1范数,当采用梯度下降方式来优化目标函数时,对目标函数进行求导,正则化项导致的梯度变化当
时取1,当
时取-1.
从而导致的参数减去了学习率与(13)式的乘积,因此当
大于0的时候,
会减去一个正数,导致
减小,而当
小于0的时候,
会减去一个负数,导致
又变大,因此这个正则项会导致参数
取值趋近于0,也就是为什么L1正则能够使权重稀疏,这样参数值就受到控制会趋近于0。L1正则还被称为 Lasso regularization。
然后针对L2范数,同样对它求导,得到梯度变化为
(一般会用
来把这个系数2给消掉)。同样的更新之后使得
的值不会变得特别大。在机器学习中也将L2正则称为weight decay,在回归问题中,关于L2正则的回归还被称为Ridge Regression岭回归。weight decay还有一个好处,它使得目标函数变为凸函数,梯度下降法和L-BFGS都能收敛到全局最优解。
需要注意的是,L1正则化会导致参数值变为0,但是L2却只会使得参数值减小,这是因为L1的导数是固定的,参数值每次的改变量是固定的,而L2会由于自己变小改变量也变小。而(12)式中的也有着很重要的作用,它在权衡拟合能力和泛化能力对整个模型的影响,越大,对参数值惩罚越大,泛化能力越好。
此外,从贝叶斯的角度而言,正则化项实际上是给了模型一个先验知识,L2正则相当于添加了一个均值为0协方差为的高斯分布先验(将L2正则表示为
),当为0,即不添加正则项,那么可以看成协方差是无穷大,
可以不受控制变成任意大。当
越大,即协方差越小,那么参数值的取值方差会变小,模型会趋向于稳定(参考[10]最高票答案)。
6. 逻辑回归与其他模型的关系
6.1 逻辑回归与线性回归
在谈两者关系之前,需要讨论的是,逻辑回归中使用到的sigmoid函数到底起到了什么作用。下图的例子中,需要判断肿瘤是恶性还是良性,其中横轴是肿瘤大小,纵轴是线性函数的取值,因此在左图中可以根据训练集(图中的红叉)找到一条决策边界,并且以0.5作为阈值,将
情况预测为恶性肿瘤,这种方式在这种数据比较集中的情况下好用,但是一旦出现如右图中的离群点,它会导致学习到的线性函数偏离(它产生的权重改变量会比较大),从而原先设定的0.5阈值就不好用了,此时要么调整阈值要么调整线性函数。如果我们调节阈值,在这个图里线性函数取值看起来是0~1,但是在其他情况下可能就是从
,所以阈值的大小很难确定,假如能够把
的值变换到一个能控制的范围那么阈值就好确定了,所以找到了sigmoid函数,将
值映射到了(0,1),并且解释成概率。而如果调节线性函数,那么最需要的是减少离群点的影响,离群点往往会导致比较大的
值,通过sigmoid函数刚好能够削弱这种类型值的影响,这种值经过sigmoid之后接近0或者1,从而对
的偏导数为
,无论接近0还是1这个导数都是非常小的。因此可以说sigmoid在逻辑回归中起到了两个作用,一是将线性函数的结果映射到了(0,1),一是减少了离群点的影响
图5 良性恶性肿瘤分类(图来源[12])
有了上面的分析基础,再来看看逻辑回归和线性回归的关系,有的人觉得逻辑回归本质上就是线性回归,它们俩都要学习一个线性函数,逻辑回归无非是多加了一层函数映射,但是我对线性回归的理解是在拟合输入向量x的分布,而逻辑回归中的线性函数是在拟合决策边界,它们的目标是不一样的。所以我不觉得逻辑回归比线性回归好,它们俩要解决的问题不一样。但它们都可以用一个东西来概括,那就是广义线性模型GLM(Generalized linear models)。先介绍何为指数簇(exponential family),当某个随机变量的概率分布可以表示为时就可以说它属于指数簇,通过调整
可以获得不同的分布。对应于线性回归与逻辑回归的高斯分布与伯努利分布就是属于指数簇的,例如取
以及
代入上式得到
。
GLM需要满足下面三个条件。
- 在给定观测值x和参数w情况下,输出y服从参数为的指数簇分布
- 预测的值
因此,选择合适的参数就能分析出线性回归和逻辑回归都是GLM的一种特例,有时会看到有的人会从GLM出发将逻辑回归的公式给推导出来。总之,线性回归和逻辑回归是属于同一种模型,但是它们要解决的问题不一样,前者解决的是regression问题,后者解决的是classification问题,前者的输出是连续值,后者的输出是离散值,而且前者的损失函数是输出y的高斯分布,后者损失函数是输出的伯努利分布。
6.2 逻辑回归与最大熵
最大熵在解决二分类问题时就是逻辑回归,在解决多分类问题时就是多项逻辑回归。为了证明最大熵模型跟逻辑回归的关系,那么就要证明两者求出来的模型是一样的,即求出来的h(x)的形式应该是一致的。由于最大熵是通过将有约束条件的条件极值问题转变成拉格朗日对偶问题来求解,模型的熵为
并假设约束条件如下,其中v,u是输出类别的index,是对应输入向量的index,是指示函数,两个值相等输出1,其他输出0。而第三个约束是通过令公式
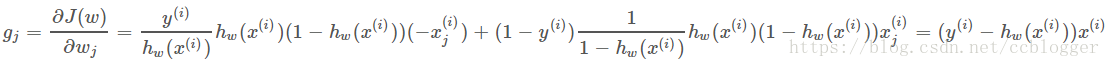
最好的取值是让每一个样本i对应
的行为接近指示函数
。
通过约束条件(15)可以直接推导出softmax的公式。基于这一点,再回过头来看《统计学习方法》上的约束条件,如果假设,公式左边的
实际上取值一直为1,那么这两个约束条件实际上是一样的。
因此,可以这样说,最大熵在解决二分类问题时就是逻辑回归,在解决多分类问题时就是多项逻辑回归。此外,最大熵与逻辑回归都称为对数线性模型(log linear model)。
6.3 逻辑回归与svm
逻辑回归和svm作为经典的分类算法,被放在一起讨论的次数特别多,这里只讨论一些我赞同的观点。
相同点:
- 都是分类算法
- 都是监督学习算法
- 都是判别模型
- 都能通过核函数方法针对非线性情况分类
- 目标都是找一个分类超平面
- 都能减少离群点的影响
不同点:
- 损失函数不同,逻辑回归是cross entropy loss,svm是hinge loss
- 逻辑回归在优化参数时所有样本点都参与了贡献,svm则只取离分离超平面最近的支持向量样本。这也是为什么逻辑回归不用核函数,它需要计算的样本太多。并且由于逻辑回归受所有样本的影响,当样本不均衡时需要平衡一下每一类的样本个数。
- 逻辑回归对概率建模,svm对分类超平面建模
- 逻辑回归是处理经验风险最小化,svm是结构风险最小化。这点体现在svm自带L2正则化项,逻辑回归并没有
- 逻辑回归通过非线性变换减弱分离平面较远的点的影响,svm则只取支持向量从而消去较远点的影响
- 逻辑回归是统计方法,svm是几何方法
6.4 逻辑回归与朴素贝叶斯
这两个算法有一些相似之处,并且在对比判别模型和生成模型,它们作为典型的分类算法经常被提及,因此这里也做一个小小的总结。
相同点是,它们都能解决分类问题和都是监督学习算法。此外,有意思的是,当假设朴素贝叶斯的条件概率服从高斯分布时Gaussian Naive Bayes,它计算出来的
形式跟逻辑回归是一样的。
不同的地方在于,逻辑回归为判别模型求的是,朴素贝叶斯为生成模型求的是
。前者需要迭代优化,后者不需要。在数据量少的情况下后者比前者好,数据量足够的情况下前者比后者好。由于朴素贝叶斯假设了条件概率
是条件独立的,也就是每个特征权重是独立的,如果数据不符合这个情况,朴素贝叶斯的分类表现就没有逻辑回归好。
6.5 逻辑回归与能量模型
基于能量的模型不是一个具体的算法,而是一种框架思想,它认为输入输出变量之间的依赖关系用一个值表示,这个值称为能量,对关系建模的这个函数叫能量函数 。如果在保持输入变量不变的情况下,对应正确输出时能量低,对应错误输出时能量高,那么这个模型就是有用的。
因此当给定了训练集S,能量模型的构造和训练由四部分组成[19]:
- 有合适的能量函数
- inference算法,针对一个给定的输入变量X和能量函数形式,找到一个Y值使得能量最小,即
- 有loss函数
,用来衡量在训练集S下能量函数的好坏
- learning算法,用来找合适的参数W,在一系列能量函数中选择让损失函数最小化的能量函数。
可以看出13步通过选择不同的能量函数和损失函数来构造不同的模型,24步是如何训练这样的一个模型。
因此当我们假设要解决二分类问题时,y取值为-1和1,如果假设能量函数为,损失函数采用negative log-likelihood loss,那么可以求得损失函数具体形式为
,这个形式与把(1)(2)代入公式(3)后得到的损失函数公式是一致的,说明这种组合下,产生的算法就是逻辑回归。因此逻辑回归是能量模型的一种特例。
而此处,同样针对二分类问题,假如能量函数保持不变,损失函数采用hinge loss,并加上一个正则化项,那么就能够推导出SVM的损失函数表达式(SVM的核函数体现在能量函数中,这里为了方便解释没有具体展开说)。这也是为什么说逻辑回归与svm最本质的区别就是损失函数不同。
【参考文献】
[1]《机器学习实战》——【美】Peter Harington
[2] Stanford机器学习公开课(https://www.coursera.org/course/ml)
[3] http://blog.csdn.net/abcjennifer/article/details/7716281
[4] http://www.cnblogs.com/tornadomeet/p/3395593.html
[5] http://blog.csdn.net/moodytong/article/details/9731283
[6] http://blog.csdn.net/jackie_zhu/article/details/8895270
[7]https://chenrudan.github.io/blog/2016/01/09/logisticregression.html









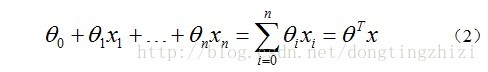
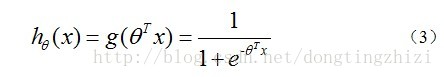
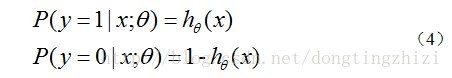
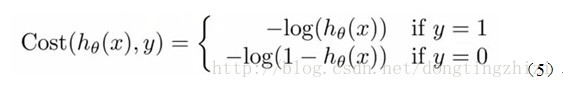
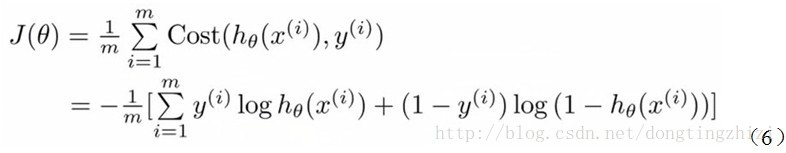
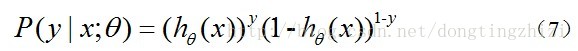
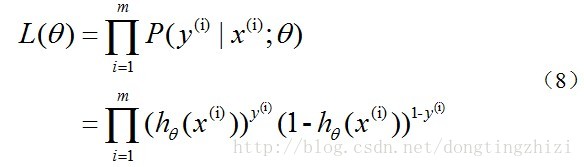
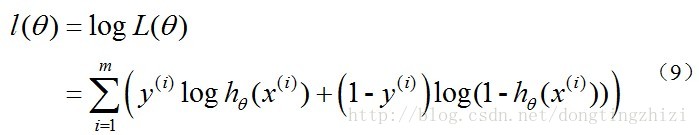

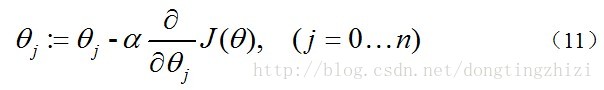
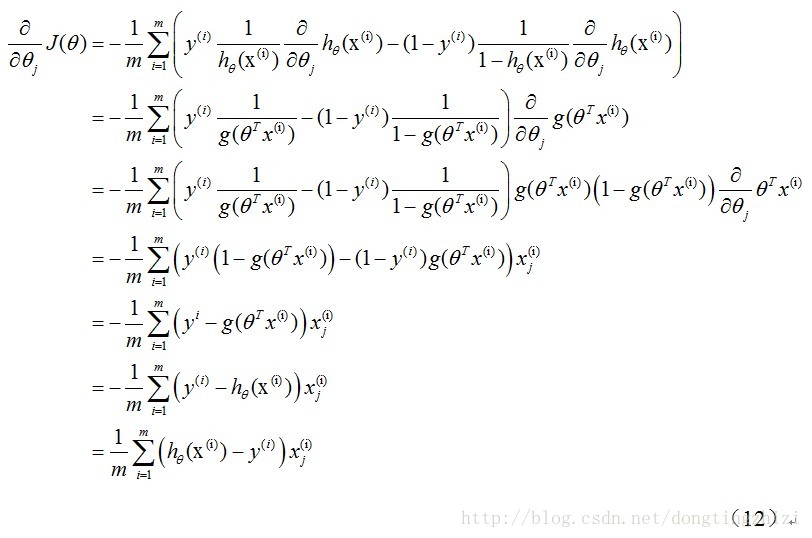
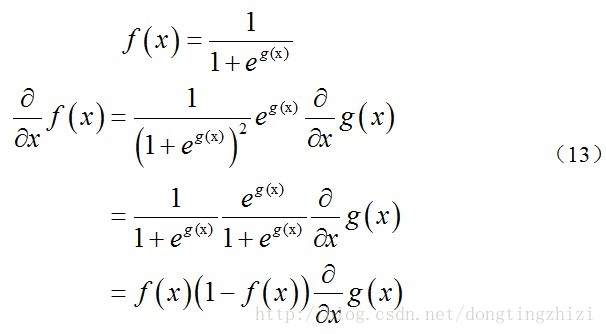
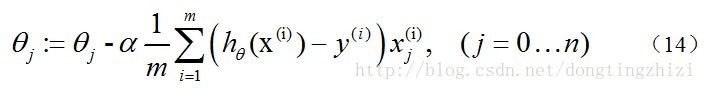
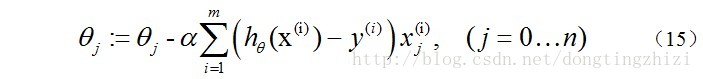
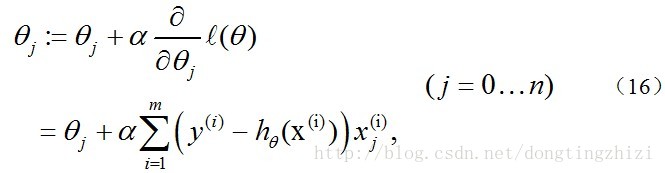
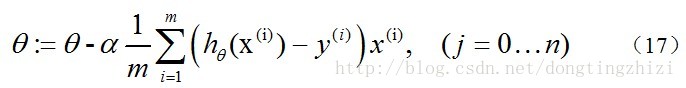
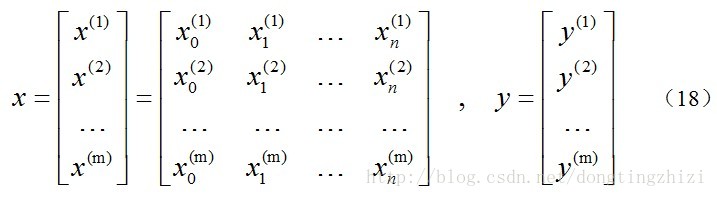
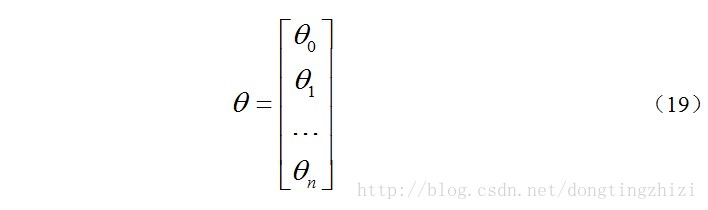

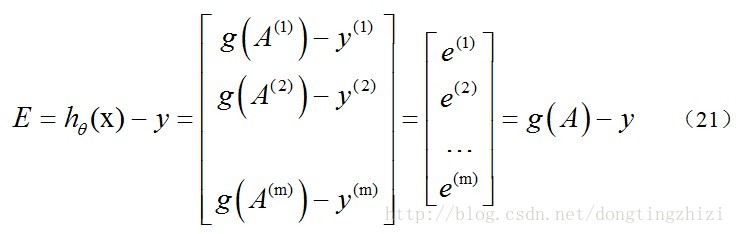
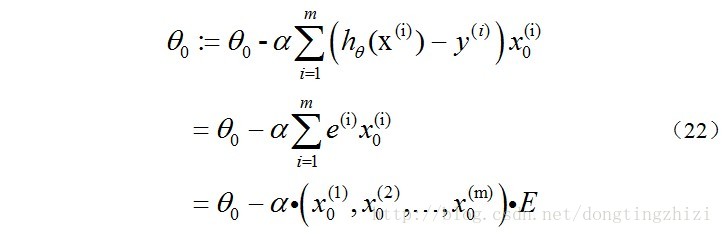
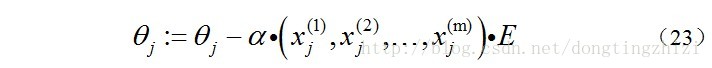
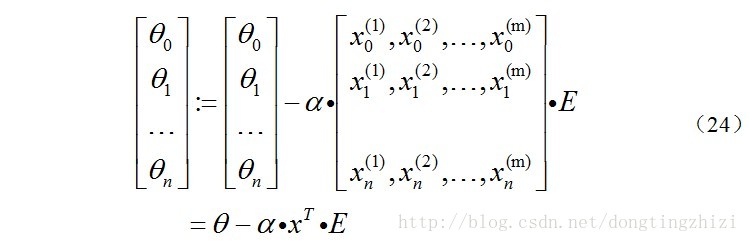
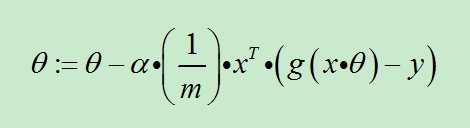
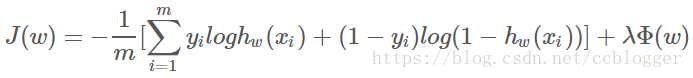
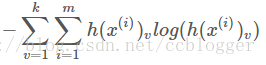
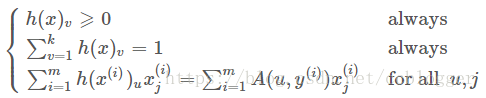
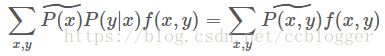













 1582
1582











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








