LeetCode_动态规划_中等_931.下降路径最小和

原创已于 2023-08-10 09:02:17 修改 · 422 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #动态规划

于 2022-03-11 21:07:17 首次发布

LeetCode 算法刷题专栏收录该内容

488 篇文章

订阅专栏

本文解析了如何使用Java实现LeetCode上的第126题“最小下降路径和”，介绍了动态规划的方法，展示了从矩阵中找到通过选择相邻元素形成下降路径的最小和的过程。

1.题目

给你一个 n x n 的方形整数数组 matrix ，请你找出并返回通过 matrix 的下降路径的最小和 。

下降路径可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

示例 1：
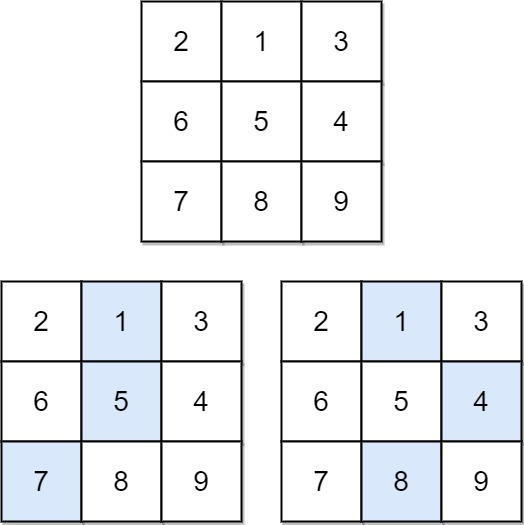
在这里插入图片描述

输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13
解释：如图所示，为和最小的两条下降路径

示例 2：
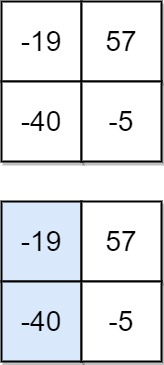
在这里插入图片描述

输入：matrix = [[-19,57],[-40,-5]]
输出：-59
解释：如图所示，为和最小的下降路径

提示：
n == matrix.length == matrix[i].length
1 <= n <= 100
-100 <= matrix[i][j] <= 100

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-falling-path-sum

2.思路

（1）动态规划

3.代码实现（Java）

//思路1————动态规划
class Solution {
	public int minFallingPathSum(int[][] matrix) {
	    int n = matrix.length;
	    // res 保存下降路径最小和，初始值为 Integer.MAX_VALUE
	    int res = Integer.MAX_VALUE;
	    // dp[i] 存储每一层对应元素的最小值
	    int[] dp = new int[n + 2];
	    //初始化 dp
	    dp[0] = dp[n + 1] = Integer.MAX_VALUE;
	    for (int j = 1; j <= n; j++) {
	        dp[j] = matrix[0][j - 1];
	    }
	    //处理每一行
	    for (int i = 1; i < n; i++) {
	        int temp = 0, last = Integer.MAX_VALUE;
	        //处理每一列
	        for (int j = 1; j <= n; j++) {
	            temp = dp[j];
	            dp[j] = Math.min(Math.min(last, dp[j]), dp[j + 1]) + matrix[i][j - 1];
	            last = temp;
	        }
	    }
	    for (int i = 1; i <= n; i++) {
	        res = Math.min(res, dp[i]);
	    }
	    return res;
	}
}