有限元学习心得（一）

自学了长达一个月的有限元，我这榆木脑瓜终于开窍了！怀着喜悦的心情分享一下学习心得：
我是按照有限元初级入门书 A First Course in Finite Elements 进行的学习。因此下面的总结中，用的图与公式都是书中的。
本次总结一下有限元一维问题：
就我看来，有限元方法就是为了求解微分方程的，因为微分方程的解太多了，用有限元方法就能找出符合微分方程的解，注意，是符合微分方程的解哦。
首先对一维的问题进行描述：

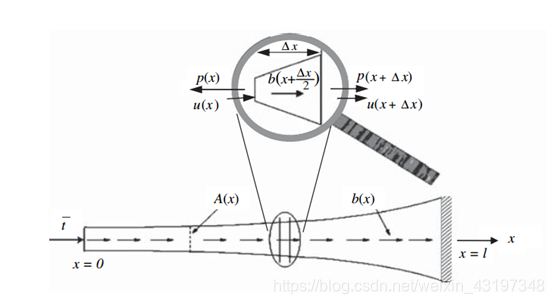
上图为一受力的杆状物，根据力的平衡得到其微分方程表达式(a)，(b)与©分别为natural boundary conditions 与essential boundary conditions，至于为何叫这个名字之后再解释。

其实上式只能代表这一种问题的描述，因为边界条件不可能只是这么固定，还有可能做一下交换，所以更为广泛的问题描述与边界条件施加为：

仔细观察上式，解u(x)是非常复杂的，因为它在式中求了两次导数，因此对于要求这种复杂解的方程，称之为强形式（strong form）。起初我也被这样硬核的叫法吓到了。
既然这样的形式不好求解，那么就想，能不能有一种很简单的solution，使他满足强形式呢？
书中给出了找出这种解的方法，即对解的要求弱一些，即求出weak form，弱形式首先第一步，给强形式换一种表达形式，

给强形式乘一个权重函数（weight function）w,再进行积分等于零。因为w的任意性（且w(l）=0)，保证了内部强形式也满足等于0的条件。上面给出了natural boundary condition, 一开始我很奇怪，essential boundary condition 去哪里了。原来这里假设，求出来的u(x)都满足essential boundary condition。这我还能说什么呢。
第二部，分部积分，为什么要分部积分呢，一开始强形式是因为要求二阶可导，也就是一阶导连续，这对solution的要求太高了，应用分部积分，使得方程中的solution解的形式弱一些。
由此得到以下方程式，这就是要求得的弱形式。

仔细观察，在弱形式中我们通过提高对权重函数w的要求来提高对solution解的要求。由强形式中要求解一阶导连续降为在弱形式中解有一阶导就可以了，注意，在弱形式得出的解中仍旧有一个非常重要的条件
u(l) = u（上面有一横）
这是为了满足essential boundary condition的，w(l）=0与natural boundary condition已经用在了弱形式中。

求得弱形式是有限元求解微分方程中非常重要的一步。可是到这里着实看不出弱形式与有限元有什么关系。

下面另起一个头，说一下有限元是怎么回事。
假设我们要分析一个杆的受力状态，如果要准确的分析，那就是求出杆上每个点的位移咯。（在力学中的求解就是求解位移，根据位移方程求解应力）但是求解每个点谈何同意，因为不论什么物体，它都有无数个点啊，要把每个点都求出来只是活在梦里罢了。所以我们现实一些，只求关键的几个点就好，整个区域上的位移根据这几个点进行插值。这就是有限元的思想。
可以看到，有限元最关键的步骤就是把求解无穷多个点降为有限个点，这个过程就叫做离散。

接下来，我们把有限元的离散与弱形式联系起来，来看一下这二者结合产生得到巨大效用。
首先对空间进行离散，因为我们举的是一维的例子，因此只需要将一个一维domain分成几个部分

用一个图像直观感受一下有限元（一维）：
如果要求解精确的solution u(x)，假设已经求出来了哦，下面就是有限元的其中一个解，注意是其中一个哦，这个强形式出来会有无穷个解的。

现在我把空间离散为3部分，再用弱形式进行求解，下面红色的线就是弱形式求出来的其中一个解。画这个粗糙的图举这个例子的原因是：有限元在离散点求出的点是准确的，而且可以简化解的形式。

下面正式开始求解：
首先求得弱形式，并将空间进行离散，得到下式：

可以看出，对空间进行离散之后，弱形式的方程就等价为在每个单元列弱形式方程，再进行累加。
其中，

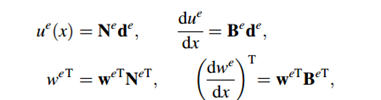
这里的de是每个单元上节点的值，N是形函数；we是每个单元的上各节点的weight 值。至于为何要让u 和w 的形函数一样，这是因为要形成稀疏矩阵，方便计算机计算，这一部分我就不说感受了，主要说有限元。
将各参数代入得到

并简化为：

这就基本完成了有限元计算的构架，书中用一个简单的例子向我们展示了计算机对上式的计算方法：

因为w1比较特殊，它因为要essential boundary ,所以w1=0
所以说只能保证r2=r3=0
用矩阵来表示

变换为：

这个方程计算机就会解了，它有三个未知数 u2 u3 与 r1,这三个未知数可以由计算机计算得出。

以上为我学习有限元的第一篇心得，很简单，有限元的思想就是离散，离散使得计算机得以计算，弱形式使得我们求解得到差不多形式的solution即可。只是一维的，虽然已经学过多维，但我对其没有太过深刻的理解，也没有编程序进行过实践，在实践过后我再写心得叭。