LeetCode Python - 70. 爬楼梯

---

题目描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。

1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

提示：

• 1 <= n <= 45

---

解法

方法一：递推

我们定义 f[i] 表示爬到第 i 阶楼梯的方法数，那么 f[i] 可以由 f[i−1] 和 f[i−2] 转移而来，即：f[i]=f[i−1]+f[i−2]

初始条件为 f[0]=1，f[1]=1，即爬到第 0 阶楼梯的方法数为 1，爬到第 1 阶楼梯的方法数也为 1。

答案即为 f[n]。

由于 f[i] 只与 f[i−1] 和 f[i−2] 有关，因此我们可以只用两个变量 a 和 b 来维护当前的方法数，空间复杂度降低为 O(1)。

时间复杂度 O(n)，空间复杂度 O(1)。

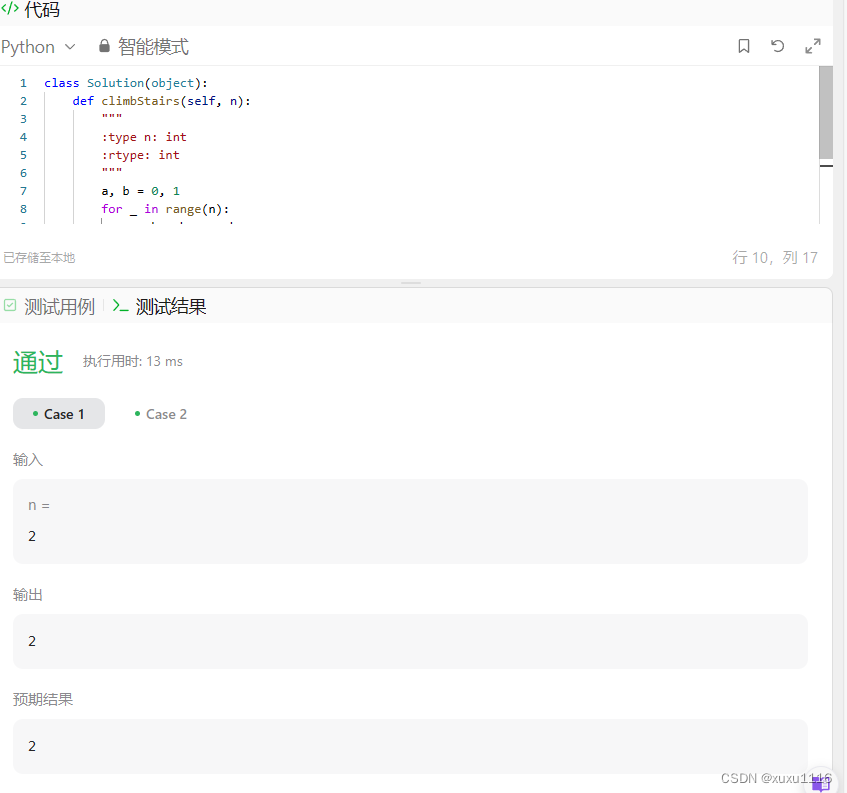
class Solution(object):
    def climbStairs(self, n):
        """
        :type n: int
        :rtype: int
        """
        a, b = 0, 1
        for _ in range(n):
            a, b = b, a + b
        return b

方法二：矩阵快速幂加速递推

我们设 Fib(n) 表示一个 1×2 的矩阵 [ F_n F_n−1 ]，其中 F_n 和 F_n−1 分别是第 n 个和第 n−1 个斐波那契数。

我们希望根据 Fib(n−1)= [ F_n-1 F_n−2 ] 推出 Fib(n)。也即是说，我们需要一个矩阵 base，使得 Fib(n−1)×base=Fib(n)，即：[ F_n-1 F_n−2 ] × base = [ F_n F_n−1 ]
​
由于 F_n = F_n-1 + F_n−2 ，所以矩阵 base 的第一列为：[ 1 1 ]

第二列为：[ 1 0 ]

因此有：[ F_n-1 F_n−2 ] × [ 1 1 1 0 ] = [ F_n F_n−1 ]

我们定义初始矩阵 res=[ 1 1 ]，那么 F_n 等于 res 乘以 base ⁿ⁻¹ 的结果矩阵中第一行的第一个元素。使用矩阵快速幂求解即可。

时间复杂度 O(logn)，空间复杂度 O(1)。

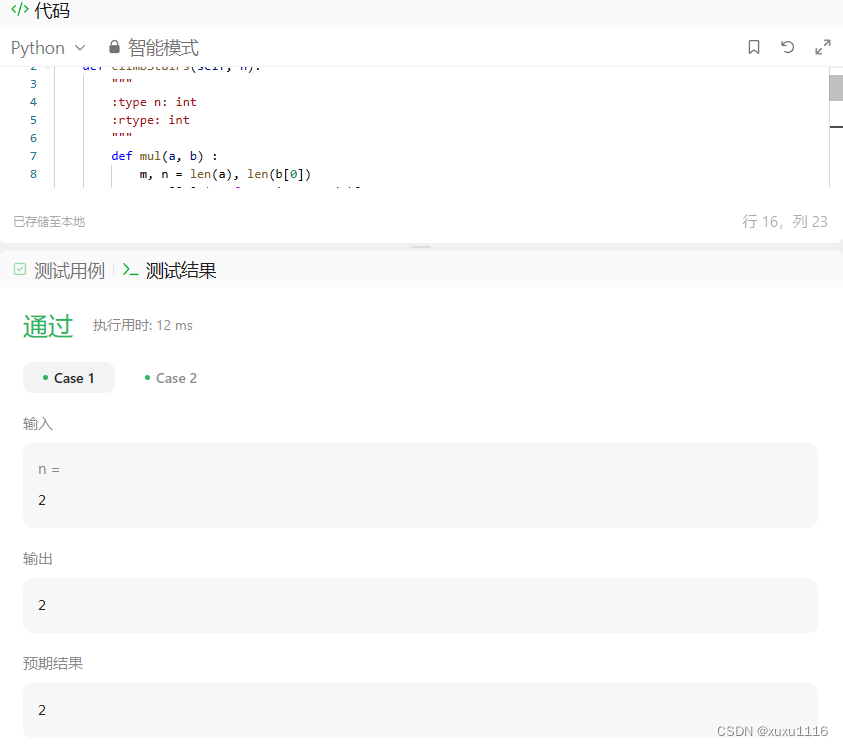
class Solution(object):
    def climbStairs(self, n):
        """
        :type n: int
        :rtype: int
        """
        def mul(a, b) :
            m, n = len(a), len(b[0])
            c = [[0] * n for _ in range(m)]
            for i in range(m):
                for j in range(n):
                    for k in range(len(a[0])):
                        c[i][j] = c[i][j] + a[i][k] * b[k][j]
            return c

        def pow(a, n) :
            res = [[1, 1]]
            while n:
                if n & 1:
                    res = mul(res, a)
                n >>= 1
                a = mul(a, a)
            return res

        a = [[1, 1], [1, 0]]
        return pow(a, n - 1)[0][0]

方法三

import numpy as np


class Solution(object):
    def climbStairs(self, n):
        """
        :type n: int
        :rtype: int
        """
        res = np.mat([(1, 1)], np.dtype("O"))
        factor = np.mat([(1, 1), (1, 0)], np.dtype("O"))
        n -= 1
        while n:
            if n & 1:
                res *= factor
            factor *= factor
            n >>= 1
        return res[0, 0]

---

运行结果

方法一

方法二

方法三