差分

一．差分攻击的背景
差分攻击是由Biham和Shamir于1991年提出的选择明文攻击方法，它的提出时间甚至比DES的设计要早十年。它是针对分组密码攻击最有效的方法之一。差分攻击通过分析特定明文差分对相对应密文差分的影响来提取密钥。差分分析现在被广泛应用于各种分组密码的攻击。
分组加密的轮数对差分分析的影响比较大。如果DES只是使用8轮的话，则在个人计算机上只需要几分钟就可以破译。但要是在完全的16轮情况下，差分分析仅比穷尽密钥搜索稍微有效。然而如果增加到17或者18轮，则差分分析和穷尽密钥搜索攻击花费同样的时间。如果再把轮数增加到19轮的话，则用穷尽搜索攻击比差分分析更容易了。差分攻击是针对对称分组加密算法提出的攻击方法，看起来是最有效的攻击DES的方法（之所以说看起来，是因为差分攻击需要很大的空间复杂度，实际上可能不如野蛮攻击具有可操作性）。2000年以前，差分攻击就被证明对MD5的一次循环是有效的，但对全部4次循环似乎难以奏效。但是随着对MD5研究的进展，情况有了变化。

二．差分攻击的描述
（1）简单的例子
一个简单的异或加密算法：

其中，c是密文，m是明文，k是密钥。可以通过密文差分来算出一对明文的差分：

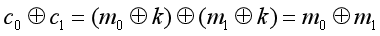
通过这种方式，我们可以从一对密文中直接得到一对明文的异或，经过一次异或运算消除了密钥。这体现了差分攻击的思想，我们可以不从单个明文和密文中考虑信息的获取，而是从一对密文和一对明文的差分入手，进行破解。实际上的密码并没有那么简单，但是依然延续了这种思想。

（2）ChiperOne
加密过程图解：

加密过程及中间状态：

此时

而由于S盒是公开的，我们可以求得S盒的逆。

此时我们可以知道：

我们可以通过猜测的值来计算出：

举例：

（3）ChiperTwo
加密流程图解：

加密过程及中间状态：

此时我们运用破解ChiperOne的方法，发现不太可行了，因为我们可以通过猜测的值算出其对应的的值，但是此时我们不能得到的值。我们可以通过

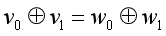
求出

的值。
同ChiperOne，我们可以得出：

但实际上：

S盒是非线性的，我们完全套用ChiperOne的方法是不可行的。
但这个S盒存在一定的输入输出差分统计规律：当输入i,j的差分为f时，结果如下表所示：

从上表可以看出，10/16的输出都是d。
所以我们可以取
，
此时正确的应当使

的概率为10/16，错误的会使其概率为1/16。

（4）ChiperThree
加密过程图解

S盒的差分分布表：

此时可以引入一个多轮的差分特征值概念，根据差分分布表，可知

的概率为10/16，

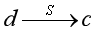
的概率为6/16。所以两轮差分特征值

的概率为10/16*6/16=15/64。此时我们可以通过和ChiperTwo类似的方法求得的值。

（5）ChiperFour
r轮，分组长度为16bit的ChiperFour加密过程：

五轮ChiperFour加密的图解：

如果可以找到一个高概率的差分特征值，理论上我们可以得到轮密钥。如果将四个S盒的输入差分都取为0，可以得到差分特征值的最高概率为16/16=1。但这对于差分分析没有意义，于是我们把其中的三个输入差分取为0，另一个输入差分取为f。
此时有

其概率为10/16。

两轮差分特征的概率为(10/16)(6/16)^3=135/4096。但由于第二轮中有三个S盒的输入差分不为0（活跃S盒），此时得到的不是最高概率的差分特征值。
我们可以找到更好的差分特征值：

概率为6/16，两轮的概率为(6/16)^2>135/4096
我们可以重复四轮这个过程。得到概率为(6/16)^4<1/16，需要改进。
此时可以发现以下几组差分轨迹都可以满足该条件：
此时概率为4(6/16)^4=81/1024>1/16。

三、差分分析的步骤

（2）差分分析的关键步骤
由r-轮迭代密码差分分析的基本过程可以发现，差分分析首先需要寻找一条高概率的差分特征，这里的高概率是指远远大于穷搜概率。
自从AES的设计者提出宽轨迹策略以来，所有新发表的分组密码在证明其关于差分分析的安全性时都用到了一个相似的原理，那就是：密码的设计者通过连续r轮加密活跃S盒个数的下界，给出了关于最优差分路径的一个非常小的上界。因此，如何找到活跃S盒个数的下界，是差分分析的关键。

四、自动化差分分析
现有文献中，混合整数线性规划（MILP）方法是求解最少活跃S盒个数最自动化的方法，通过建立模型、编写程序生成关于差分传播模式的MILP实例，即可实现最少活跃S盒个数的自动化求解。与其它方法相比，该方法需要更少的工作量。
4.1 MILP问题
MILP问题是指一类从线性规划发展来的优化问题，旨在找出一个线性的目标函数在某些线性限制下的最优解。尽管MILP问题和许多离散优化问题有密切的联系，诸如集合覆盖问题，0-1背包问题和推销员旅行问题，但是它直到近几年才被应用于密码学的研究上。
MILP问题可描述如下：

4.2 Mouha等人提出的框架及其扩展
4.2.1 Mouha等人基于字级（word-oriented）分组密码提出的框架
Mouha等人通过建立MILP模型，自动确定字级分组密码算法中活跃S盒个数的下界。下面给出该方法的简要描述。

Mouha等人提出的框架中，用0-1变量表示字级差分在密码算法中的扩散，变量取值为1表示非零差分，取值为0表示零差分，这些0-1变量满足上述三种运算所对应的限制条件。
1.异或运算的约束表达式

2.线性变换的约束表达式

3.MILP模型目标函数的表示

4.2.2 Mouha等人提出的框架在比特级分组密码上的扩展
比特级的SPN结构的分组密码算法，主要包括异或运算、S盒代换层及P置换扩散层三种运算。其中，扩散层不产生新的约束条件，只是将上一层约束条件中的变量进行了置换。因此，我们只需总结出两类约束表达式：一类是异或运算应满足的约束条件，另一类则是S盒代换应满足的约束条件。此外，为使最少活跃S盒个数不为0，需增加一些新的约束。
1.异或运算的约束表达式
将前面所描述的字级约束表达式转化到比特级后，异或操作的约束表达式是一致的，见表达式（4-3）。
2.S盒代换的约束表达式


3.其他约束

4.0-1约束
目前为止，所有引入的变量都是0-1变量，因此前面提到的MILP模型实际上是一种纯整数线性规划问题。但在实际应用中，为节省求解时间，我们只要求表示明文差分的变量及所有的哑变量为0-1变量，其他变量的取值为实数，这就成了一般的MILP问题，在很大程度上节省了问题的求解时间。
5.MILP模型目标函数的表示
将前面所描述的字级约束表达式转化到比特级后，目标函数的表达式是一致的，见表达式（4-5）。

研究步骤：
1.建立寻找PRESENT算法高概率差分特征的MILP模型
Step 1. 建立MILP模型的变量：利用若干0-1变量表示PRESENT算法加密过程中每一个比特级的差分，当该处有差分时变量取值为1，反之为0。依据的原则是使得引入变量的个数最少。
Step 2. 建立MILP模型的约束：将差分比特经过异或、S盒代换层（非线性层）和P置换层产生的约束分别用线性不等式表示出，即为变量应满足的约束。
Step 3. 对约束不等式进行自动化筛选，筛选的目标是：能够剔除的不可能差分对最多的那n个不等式
Step 4. 建立MILP模型的目标函数：将加密过程中涉及到的S盒用0-1变量Aj表示，当S盒活跃时，Aj取值为1；反之，取值为零。目标函数为：

，即使得活跃S盒个数最少。

2.对PRESENT算法进行自动化差分分析
根据1中的步骤，建立PRESENT算法低轮加密的MILP模型，通过Python编程生成Gurobi求解软件可识别的文件，并对该文件进行求解，得到PRESENT的一条高概率差分特征；逐渐增加轮数，分别求得相应轮数的一条高概率差分特征。
分别计算各差分特征的概率并与穷搜结果进行对比，给出对PRESENT算法进行自动化差分分析的结论。 以PRESENT算法举例PRESENT加密过程图解：

PRESENT的轮函数

表4-1 PRESENT算法S盒的差分分布表

表格的第i行第j列表示当S盒的输入差分为时输出差分为的频数，频数除以16即为相应差分的概率。从表格中可看出，当输入差分不为0时，输出差分的最大频数为4，即输出差分的概率不超过1/4，这是PRESENT算法S盒的一个重要的性质。

表4-2 PRESENT-80单密钥差分分析结果


从表4-2可看出，PRESENT-80单密钥模型的全轮MILP实例包含1056个0-1变量，1984个连续变量，7937个约束。这个实例可以在222秒内求解，解得的最少活跃S盒个数为62。由于PRESENT算法S盒差分的最大概率为1/4，因此，全轮PRESENT-80的单密钥差分特征的最大概率不超过2^-2*62，其小于穷搜概率2^-80，因此我们认为PRESENT-80在抵抗单密钥差分分析时是安全的.