前言：
根据《2025年张宇30讲》，整理的重点的，需要加强记忆的知识点。
目录
第1讲 函数极限
1.1 奇偶和周期
1.1.1 函数的奇偶性
1.1.2 函数的周期性
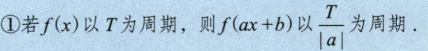
下面例题：函数可导，导函数有界，怎么证明其函数有界？
1.2 函数图像
头脑闪现下列图像
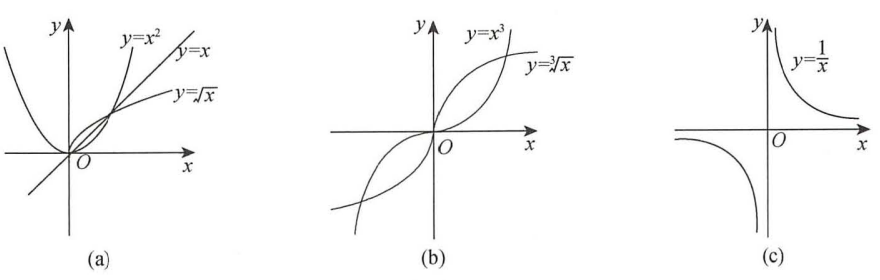
求下面的值并几何理解：
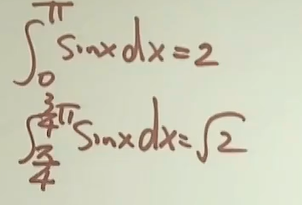
1.3 三角函数
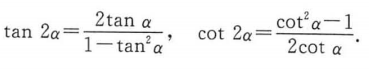
1.4 常用不等式
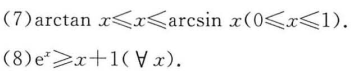
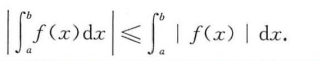
例题1：
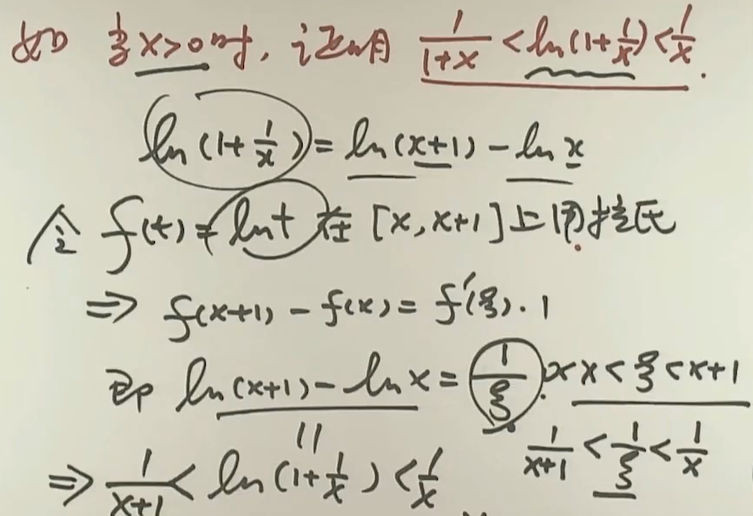
例题2：求下列的界限
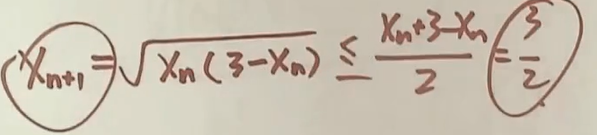
1.5 函数极限的定义
函数极限存在的充要条件：
1.6 泰勒公式
1.7 无穷小运算规则
来个例题：
1.8 无穷小的比阶
1.9 等价无穷小替换
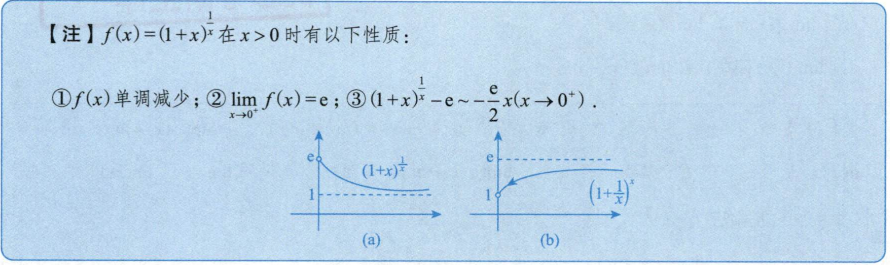
1.10 函数的连续和间断
10.1 函数连续的定义
10.2 间断点的定义与分类
10.3 重点记忆
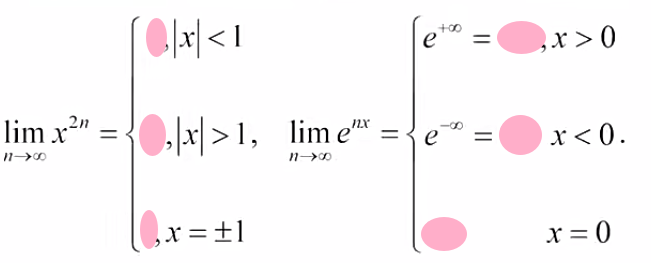
抓大头的事项：
1.11 函数极限的保号性
第2讲 数列极限
2.1 求数列
2.2 数列极限定义
2.3 单调有界准则
2.4 重点记忆
2.4.1 重点1
2.4.2 重点2
2.4.3 重点3
2.3.4 重点4
2.4.5 重点5
2.4.6 重点6
第3讲 一元微分学的概念
3.1 导数的定义式
3.2 导数的提法
3.3 可导的充要条件
3.4 函数和导数关于有界
若f(x)的导数是有界，函数f(x)是否有界。
不一定：举反例：f(x)的导数为y=1，则f(x)=x无界。
若f(x)的导数在有限区间有界，函数f(x)一定有界。（拉格朗日证明）
3.5 判别可微
通常首要看是否可导，如果可导必可微，可微也必可导。
或者：
第4讲 一元微分学的计算
4.1 求导基本公式
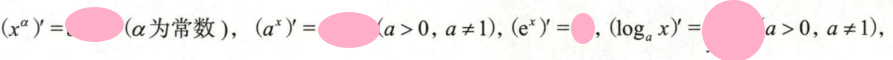
4.2 反函数的求导
4.2.1 一阶反函数求导
4.2.2 二阶反函数求导
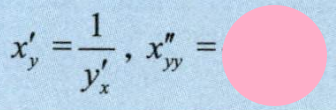
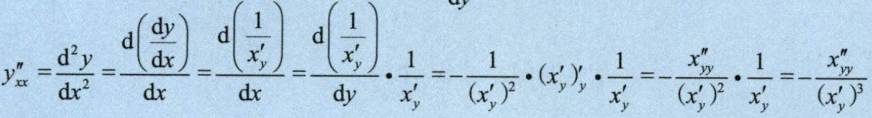
4.3 求高阶导数
4.4 泰勒展开式
4.5 莱布尼茨公式
第5讲 一元微分学几何应用
5.1 极值的定义
注意下列情况也存在极值：
存在极值的两种情况： 
5.2 单调和极值的判别
5.3 图像凹凸性
5.4 图像拐点
5.5 极值点和拐点的结论
5.6 函数的渐近线
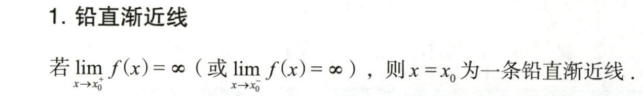
5.7 函数的图像
关于对称
5.8 曲率和曲率半径
第6讲 中值定义和微分不等式
6.1 涉及函数的中值定义
6.2 涉及导数的中值定理
6.2.1 费马定理
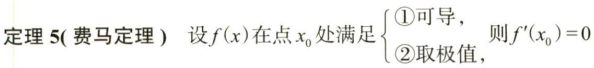
6.2.2 罗尔定理
罗尔定理的使用 
6.2.3 拉格朗日定理
6.2.4 柯西定理
6.2.5 泰勒公式
6.3 微分等式
6.4 微分不等式
第7讲 一元微分物理应用
7.1 物理应用
7.2 相关变化率
第8讲 一元函数积分学的概念和性质
8.1 不定积分存在定理
8.2 定积分存在定理
8.3 变限积分的性质
8.4 反常积分的敛散性
重要的推广
重要的不等式
第9讲 一元函数积分学的计算
9.1 基本积分公式
9.2 点火公式
第10讲 一元积分学的几何应用
10.1 平面图像的面接
10.2 旋转体的体积
10.3 平面曲线的弧长
10.4 旋转曲面的面积
10.5 形心坐标公式
第11 讲 积分等式和积分不等式
11.1 推广的积分中值定义
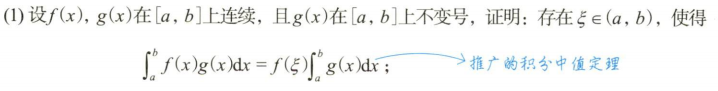
第 12 讲 积分的物理应用
12.1 变力直线做功
12.2 抽水做功
12.3 静水压力
第13讲 多元函数微分学
13.1 多元函数求极限
- 一般的分子的次数大于分母为0
- 一般的分子的次数不大于分母无穷或不存在
- 利用不同路线去求极限
下面的都为0；
下面为不存在：
13.2 多元函数可微的几何意义
13.3 二元函数可微及两种表达形式
13.4 可微的判别
13.5 可微与极限的关系
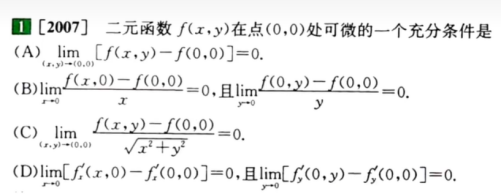
- A：连续不一定可微
- B：偏导存在也不一定可微
- C：正确，先求出偏导数都是0，然后根据定义可知可微
- D：偏导连续是x->0,y->0
第14讲 二重积分
二重积分是多元微积分中的一个重要概念，用于计算二维区域上的函数积分。它通常用于计算平面区域上的面积、质量、重心等问题。二重积分的基本思想是将一个二维区域分割成无数个小区域，然后在每个小区域上计算函数值的积分。
14.1 二重积分的定义
设 f(x,y)f(x,y)是定义在平面区域 D 上的函数，二重积分记作：,其中 dA表示面积元素。
14.2 二重积分的几何意义
如果 f(x,y)是非负函数，二重积分 表示以 D 为底、以 f(x,y)为顶的曲顶柱体的体积。
14.3 二重积分的计算步骤
直角坐标系
极坐标系
最后：考前记忆
16.1 点到直线的距离公式
16.2 下列积分的值
扫一扫
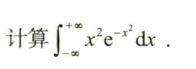
2万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
