动态规划-----矩阵连乘(java)

（写在前面）哦豁，一天搞一个算法。(￣ω￣;)

一、问题

设有6个矩阵A1A2A3A4A5A6相乘，即n=6，然后它的维数可组成矩阵p[ ]（p的长度为n+1）。问题为矩阵数乘最小次数为多少？

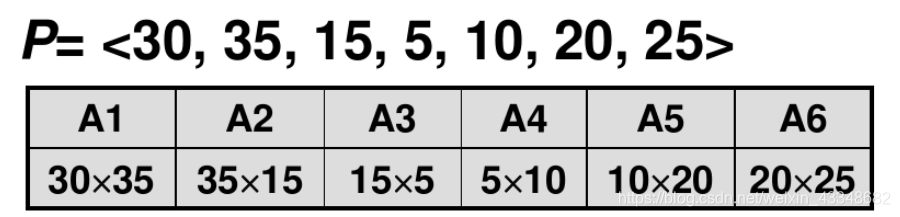
二、图示

下面的图反应了不能使用递归的原因，因为大问题包含小问题，递归算法许多子问题会被重复计算，递归算法的时间复杂度为O(2^n)，灾难级别的复杂度。

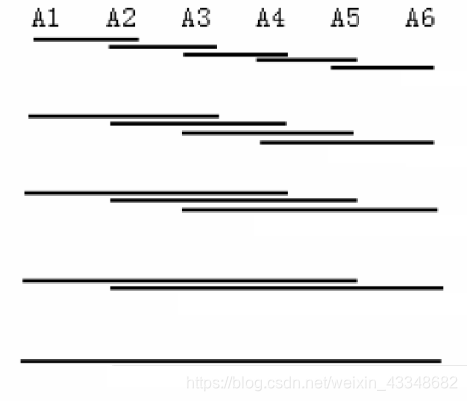
三、

引出动态规划，每个子问题只计算一次，计算后存起来，用到时再调用。动态规划算法的时间复杂度为O(n^3)。

四、java代码

 
代码有详细解释!！
 

public class MatrixChain {
   
   
    public static void MatrixChain(int[] p, int n, int[][] m, int[][] s) {
   
   
        /*①p为矩阵的行与列数，注意若矩阵的个数为n个，则p.length=n+1,两两相乘，中间有n-1个，加上两边2个，共n+1个，
        即数组p的长度为n+1。这里p[]存储p[0]、p[1]、p[2]......p[n]。
        ②n为矩阵的个数。
        ③m[i][j]为A[i:j]的最少数乘次数，即AiAi+1......Aj连乘的最少次数。
        ④s[][]为存放插入点位置的*/
        for (int i = 1; i <= n; i++) {
   
   //把对角线的都设为0，因为单个矩阵与自己无法相乘。
            m[i][i] = 0;
        }
        for (int r = 2; r <= n; r++) {
   
   //① r为矩阵连乘的长度，从2开始，好戏开始了。② r的引入也改变了i与j的下标。
            for (int i = 1; i <= n - r + 1; i++) {
   
   //确定i的下标，这里减一是因为r=2。
                int j