【Leetcode刷题】【动态规划】

动态规划

在此之前，先复习一下递归和分治，直接看代码模板：
递归：

分治：

而动态规划实际上就是分治加上最优子结构，动态规划和递归与分治没有根本上的区别（关键是看有无最优子结构），下面结合一个例子来理解：

62不同路径

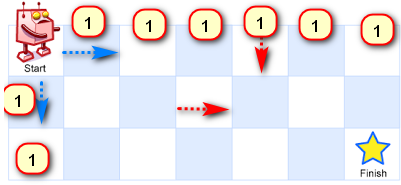
我们可以看一下这个问题，需要找到从左上角到右下角有多少种可能路径，首先看一下能否找出最优子结构，

到图中（i,j）这个点有多少种走法，实际上相当于start到左边点的走法加上start到上边点的走法，所以可以写出状态转移方程：

dp[i,j]=dp[i-1,j]+dp[i,j-1](i>=1,j>=1)

第二个看边界条件，我们可以发现最左列和最上边都是只有一种走法

dp[0][j] = 1，dp[i][0] = 1

因为题目要求只能往右走一步或往下走一步，最下边和最右列如下

class Solution {
    public int uniquePaths(int m, int n) {
           int [][]dp=new int [m][n];

           for(int i=0;i<m;i++){
               dp[i][0]=1;
           }

           for(int j=0;j<n;j++){
               dp[0][j]=1;
           }
           for(int i=1;i<m;i++){
               for(int j=1;j<n;j++){
                   dp[i][j]=dp[i-1][j]+dp[i][j-1];
               }
           }

           return dp[m-1][n-1];
    }
}

63不同路径II

这里添加了障碍物，我们在初始化边界的时候要注意判断边界上的格子是否有障碍物，如果有障碍物就不需要初始化跳过，同样在状态方差时也要保证当前位置不是障碍物。

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        //dp表记录的是到i,j最多有几条路径
        int[][] dp = new int[m][n];
        int i = 0;
        //左边界在不遇到障碍物时只有唯一路径
        while (i < m && obstacleGrid[i][0] != 1) {
            dp[i][0] = 1;
            i++;
        }
        int j = 0;
        //上边界在不遇到障碍物时只有唯一路径
        while (j < n && obstacleGrid[0][j] != 1) {
            dp[0][j] = 1;
            j++;
        }
        for (int p = 1; p < m; p++) {
            for (int q = 1; q < n; q++) {
                //保证当前位置不是障碍物
                if (obstacleGrid[p][q] != 1) {
                    //动态方程
                    dp[p][q] = dp[p - 1][q] + dp[p][q - 1];
                }
            }
        }
        return dp[m - 1][n - 1];
    }
}

1143最长公共子序列

我们可以从两个字符串的最后一个字符开始往前判断，若最后字符相同，则两个字符串都减去最后一个，求他们的公共子序列，再加1；若不相同，则第一个字符串减去一，或者第二个字符串减去一，再求他们的最长公共子序列中的最大值，所以DP方程为：

如果A[i]==B[j]，那么dp[i][j]=1+dp[i-1][j-1]
如果 A[i] != B[j]，那么 dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1])

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
           int m=text1.length();
           int n=text2.length();
           int [][]dp=new int [m+1][n+1];
           for(int i=1;i<m+1;i++){
               for(int j=1;j<n+1;j++){
                   if(text1.charAt(i-1)==text2.charAt(j-1)){
                       dp[i][j]=1+dp[i-1][j-1];//如果两个子串最后一个字符相同，则返回1+前一个子串的最长公共子长度
                   }
                   else{
                       dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);//不相同则要不第一个字符串减去一个，要不第二个字符串减去一个，求他们的最长公共子序列加1
                   }
               }
           }
           return dp[m][n];
    }
}

120三角形最小路径和

DP方程的三步确定法：
1.找重复性
2.定义状态数组
3.写出dp方程
我们可以看到，每一个元素都等于当前元素值加上下一行元素的当前位置和后一个位置最小值之和，可以写成：

f(i,j)=min[f(i+1,j),f(i+1,j+1)]+a[i,j]

进行状态定义：
dp[i] [j]表示包含第i行第j列元素的最小路径和
状态分析
初始化：
dp最后一行=triangle最后一行
常规：
triangle[i][j]一定会到达triangle[i+1][j]或者triangle[i+1][j+1],
所以状态dp[i][j]一定等于dp[i+1][j]或者dp[i+1][j+1]的最小值+triangle[i][j]
转移方程：

dp[i][j]=min(dp[i+1][j],dp[i+1][j+1])+triangle[i][j]

自底向上递归比较容易找到最优解

    public int minimumTotal(List<List<Integer>> triangle) {
        // 特判
        if (triangle == null || triangle.size() == 0) {
            return 0;
        }
        // dp中记录了求第i行时，第i+1的最小路径和，加一可以不用初始化最后一行
        int[] dp = new int[triangle.size() + 1];

        for (int i = triangle.size() - 1; i >= 0; i--) {
            List<Integer> rows = triangle.get(i);
            for (int j = 0; j < rows.size(); j++) {
                dp[j] = Math.min(dp[j], dp[j + 1]) + rows.get(j);
            }
        }
        return dp[0];
    }

53最大子序和

1.定义DP函数
猜测是为以nums[i]结尾的最大子序和
2.数学归纳法可以得到

dp[i] = Math.max(dp[i-1], 0)+nums[i];

也就是判断当前位置之前的最大子序和是否大于0，大于0则加上当前位置元素，小于0就前面最大子序和为0；
3.最后返回dp数组中值最大的

class Solution {
  public int maxSubArray(int[] nums) {
        int m=nums.length;
        //定义dp  为 以nums[i]结尾的最大子序和
        int[] dp = new int[m];
        dp=nums;
        for (int i = 1; i < dp.length; i++) {
            dp[i] = Math.max(0,dp[i-1])+nums[i];
        }

        //所以最后的值就是在dp所有的值中选最大的
        int res = nums[0];
        for (int i = 0; i < dp.length; i++) {
            res = Math.max(res , dp[i]);
        }
        return res;
    }
}

198打家劫舍

//1.重复子问题
//2.状态定义 a[i]从0到第i号位置能偷到的最大金额
//3.DP方程 a[i][0]=Math.max(a[i-1][0],a[i-1][1]);
//a[i][1]=a[i-1][0]+nums[i];


class Solution {
    public int rob(int[] nums){
        if(nums==null||nums.length==0){
            return 0;
        }
        int n=nums.length;
        int[][]a=new int [n][2];

        a[0][0]=0;//0代表不偷
        a[0][1]=nums[0];//1代表偷；

        for(int i=1;i<n;i++){
            a[i][0]=Math.max(a[i-1][0],a[i-1][1]);//0表示不偷，则其值为前一个位置偷或者不偷两者的最大值
            a[i][1]=a[i-1][0]+nums[i];//1表示偷，则为前面一个位置不偷的值加上当前位置的值
        }
        return Math.max(a[n-1][0],a[n-1][1]);
    }
}

将二维转变为一维

//1.重复子问题
//2.状态定义 a[i]从0到第i号位置能偷到的最大金额,
//3.DP方程


class Solution {
    public int rob(int[] nums){
        if(nums==null||nums.length==0){
            return 0;
        }
        if(nums.length==1){
            return nums[0];
        }
        int n=nums.length;
        int[]a=new int [n];

        a[0]=nums[0];//初始化
        a[1]=Math.max(nums[0],nums[1]);//初始化
        int res=Math.max(a[0],a[1]);//初始化
        for(int i=2;i<n;i++){
            a[i]=Math.max(a[i-1],a[i-2]+nums[i]);//前一个位置偷，则当前位置不偷，所以前一个位置偷的最大金额等于当前位置偷的最大金额，若前一个位置不偷，则当前位置偷的金额加上前两个位置偷的金额之和
            res=Math.max(a[i],res);
        }
        return res;
    }
}