剑指offer(C语言)3-10

3-1 数组中重复的数字

题目：在一个长度为n的数组里的所有数字都在0~n-1的范围内。数组中某些数字是重复的，但不知道几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。例如，如果输入长度为7的数组｛2，3，1，0，2，5，3｝那么对应输出是1或者3

思路：方法有很多，比如说先排序。但是完全可以在时间复杂度为O(N),空间复杂度是O(1)的条件下实现。
如果没有重复的 说明0-N中的每一个数都有，可以把每个数放在下标为该数的位置，比如0放在number[0],1放在number[1].而且每个数所以可以从第一个开始，把每个数和这个数该在的位置替换位置，如果发现那个位置的数和自己相等，则返回。

#include <stdio.h>
#define bool unsigned int
#define true 1
#define false 0
#define none 2
 bool Duplicate(int numbers[],int length,int *duplicate)
{
	int i = 0;
	int swap =0;
	if(numbers == NULL || length<=0)
	{
		return false;
	}
	for (i = 0;i < length; i++)
	{
		if(numbers[i]<0 || numbers[i]>=length)
			return false;
	}
	for(i = 0;i<length ; i++)
	{
		while(numbers[i]!=i)
		{
			if(numbers[i] == numbers[numbers[i]])
			{
				*duplicate = numbers[i];
				return true;
			}
			swap = numbers[i];
			numbers[i] = numbers[numbers[i]];
			numbers[numbers[i]] = swap;
		}
	}
	return none;
}
int main()
{
	int numbers[6] = {1,0,2,3,4,4};
	int length = sizeof(numbers)/4;
	int duplicate = -1;
	bool state = Duplicate(numbers,length, &duplicate);
	printf("%d,%d",state,duplicate);
}

3-2 数组中重复的数字（不能修改数组)

题目：在一个长度为N+1的数组里的所有数字都在1~n范围内，所以数组中至少有一个数字是重复的。请找出数组中任意一个复杂的数字，但不能修改输入的数组。
思路：这道题很简单，因为有很多种解法。但是不同的解法对应不同的时间复杂度和空间复杂度，要根据面试官要求写出他想要的程序。
1.新建一个数组，对该数组进行排序。比如插入排序，时间复杂度是O(N2).排完序找重复的数就很简单了，空间复杂度是O(N)
2.第一种方法时间复杂度可以通过改善排序算法降低，但是空间复杂度无法降低。书中提出了一种可以不额外开辟空间的算法，思路如下：由于数组是有规律的，所有数都在1~n内，有n+1个数。把数字分为两部分（根据数值大小），1 ~ m, m+1 ~ n.一定有一个范围内的数比该区间的大小大1（1 ~m应该有m个数，m+1就有问题 ）。一直折半，最后当区间范围的头和尾部相等时，就找到了。
最开始不太好想，可以想象一个盒子里全是红球，有一个黑球，然后把盒子不断分成一半，而你又能判断黑球在哪一半。一直分到最后，自然就出来了。
这种方法有个问题：就是不能找到所有重复的数，｛1，1，3，4，5，5｝这种只能找到4，因为第一次分半时就和把重复的1当做2的情况一样了，让他安全了。
空间复杂度是O(1),看一下时间复杂度怎么算，最开始范围是n,最后范围大小是1，每次一半，所以2的x次方等于n，x = log2(n),范围二分过程的时间复杂度是log2(n).每次分完要判断整个数组中所有数是否在该范围内，O(n).所以最后总时间复杂度为O(nlog(n)）

#include <stdio.h>
#define bool unsigned int
#define true 1
#define false 0
#define none 2

int GetCount(int start,int end,int length,const int *numbers)
{
	int i = 0;
	int count = 0;
	for(i = 0;i<length ; i++)
	{
		if(numbers[i]>=start && numbers[i]<=end)
			count ++ ;
	}
	return count;
}
bool Duplicate(const int* numbers,int length,int *deplicate)
{
	int start = 1;
	int end = length - 1;
	int middle;
	int count;
	int i;
	if(numbers ==0 || length == 0)
		return false;
	for(i=0;i<length;i++)
	{
		if(numbers[i]>length-1 || numbers[i]<=0 )
			return false;
	}
	while(1)
	{
		middle = (start + end)/2;
		count = GetCount(start,middle,length,numbers);
		/*
		if(count>(middle - start + 1))
			end = middle;
		else
			start = middle+1;*/
		if(end <= start)
		{
			if(count>1)
			{
				*deplicate = start;
				return true;
			}
			else
				return false;
		}
		
		if(count>(middle - start + 1))
			end = middle;
		else
			start = middle+1;
	}
}
int main()
{
	int numbers[] = { 3, 2, 1, 4, 4, 5, 6, 7 };
	int length = sizeof(numbers)/4;
	int duplicate = 0;
	bool state = Duplicate(numbers,length, &duplicate);
	printf("%d,%d",state,duplicate);
}

代码有一个地方要注意：GetCount函数之后必须直接判断end<=start。
{ 3, 2, 1, 4, 4, 5, 6, 7 }为例：
循环几次之后，start = 3,end = 4,middle = 3.GetCount得到1，start变成4，这时候end<=start条件满足，进入判断，但是count=1;出错。
也就是说，在判断之前必须得到的是最新的GetCount。这个BUG很难发现,大多数情况是不会出问题的。

4 二维数组中的查找

题目：在一个二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序，请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。
思路：将数组看成一个矩阵，从左下角或者右上角开始，以左上角为例，若小于该数则行 ++，如果大于该数则列–。终止条件为找到等于该数或者到了右下角。
注意：
1.二维数组在定义时不能省略列数（后面那个）
2.二维数组传递到子函数中，常用的有两种方法。
一种是直接传入二维数组（本身是二维指针）
int matrix[][4]；
bool result = Find(matrix, 4, 4, number);
bool Find(int matrix[][4], int rows, int columns, int number)；
这种方法的缺点是子函数必须知道传入的二维数组的列数是多少，如果把4改成5编译会通过，但是实际上的内容就错了。
第二种方法是将二维数据降级为一级指针，然后将二维数组看成一维数组int matrix[][4]；
bool result = Find((int*)matrix, 4, 4, number);
bool Find(int* matrix, int rows, int columns, int number)；
这种方法的缺点是无法用a[i][j]这种方式查询数组了，要用a[i*colums+j]来查询。

#include <stdio.h>
#define bool unsigned int
#define true 1
#define false 0
#define none 2

bool Find(int* matrix, int rows, int columns, int number)
{
	int i = 0;
	int j = columns-1;
	while(i<rows && j>=0)
	{
		if(matrix[i*columns+j] == number)
		{
			return true;
		}
		else if(matrix[i*columns+j]>number)
			j--;
		else
			i++;
	}
	return false;
	
}
int main()
{
	int matrix[][4] = {{1, 2, 8, 9}, {2, 4, 9, 12}, {4, 7, 10, 13}, {6, 8, 11, 15}};
	int number = 4;
	bool  result = Find((int*)matrix, 4, 4, number);
	printf("%d",result);
}

5 字符串替换空格

题目：请实现一个函数，把字符串中的每个空格替换成%20.
基本思路：这道题的问题在于要把一个字符的空格变成三个字符的%20，所以要改变字符串。常规思路就是从头开始查找，找到空格后把后面的字符向后移动两位然后把这三个位置替换为%20.
时间复杂度为O（n2）.
优化思路：上面思路的时间主要浪费在每次找到空格都要移动后面的字符串。可以先一次性找出空格的数量，这样字符串的新长度就能确定了，由于字符串的后面是空的，所以可以从后向前复制，两个指针，p1指向新长度的最后，p2指向老字符串的最后。然后不断判断老字符串，如果不是空格就复制过去，是空格就把%20写过去。
停止条件：p2 = p1(p2=p1说明前面已经没空格了)
时间复杂度为O(n)
注意：
1.字符串的两种定义，char * str = “csh”;char str[] = “csh”.两种方法是不一样的。C语言会把字符串放到只读存储区，第一种方式会指向该位置，第二种方式会在数据区分配一段区域，然后把字符串复制过去。因为程序要改变字符串，所以必须用char str[]="csh"的方式，否则程序会崩溃。
2.字符串结束的标志是‘\0’，不要忘记。否则会出现乱码。

#include <stdio.h>
#include <stdlib.h>
#define bool unsigned int
#define true 1
#define false 0
#define none 2


bool ReplaceSpace(char* str,int length)
{
	char* p1,*p2;
	int originalLength = 0;
	int newLength = 0;
	int spaceNum = 0;
	int i = 0;

	if(str == 0)
		return false;
	while(str[i]!= '\0')
	{
		originalLength ++;
		if(str[i] == ' ')
			spaceNum++;
		i++;
	}
	newLength = originalLength + spaceNum*2 ;
	
	if(newLength > length)
		return false;

	p1 = &str[originalLength];
	p2 = &str[newLength ];

	//while(p1>=&str[0] && p2>p1)
	while (p2>p1)
	{
		if(*p1 == ' ')
		{
			*p2-- = '0';
			*p2-- = '2';
			*p2-- = '%';
		}
		else
			*p2-- = *p1;

		p1 --;
	}
	return true;
}
int main()
{
	const int length = 100;
    char str[100] = " We are happy ";
	//char *str = " We are happy ";
    bool state = ReplaceSpace(str, length);
	if(state)
	{
		printf("%s",str);
	}
}

6 链表反向打印

题目：输入一个链表的头结点，从未到头打印出每个节点的值
思路 1.放到栈里 打印栈。2.递归
（C语言需要自己写链表，锻炼以下功底吧）

#include <stdio.h>
#include <stdlib.h>
#define bool unsigned int
#define true 1
#define false 0
#define none 2

typedef struct ListNode
{
	int data;
	struct ListNode* next;
}listNode;

bool NodePush(listNode* L,int data)
{
	listNode* p;
	listNode* node = (listNode*)malloc(sizeof(listNode));
	if(!node)return false;
	node->data = data;
	node->next = NULL;
	p = L;
	while(p->next!=NULL)
		p = p->next;
	p->next = node;
	return true;
}

listNode HeadCreat(int data)
{
	listNode head ;
	head.data = data;
	head.next = NULL;
	return head;
}
void PrintListReverse(listNode* head)
{
	int stack[40];
	int i = 0;
	listNode* p = head;
	if(head == NULL)return;
	while(p->next!=NULL)
	{
		stack[i++] = p->data;
		p = p->next;
	}
	stack[i] = p->data;
	for(;i>=0;i--)
	{
		printf("%d ",stack[i]);
	}
	printf("\n");

}

void PrintListReverse1(listNode* head)
{
	if(head == NULL)return;
	if(head->next!=NULL)
		PrintListReverse1(head->next);
	printf("%d ",head->data);
}
int main()
{
	int i;
	listNode node = HeadCreat(4);
	listNode* head = &node;
	for(i=5;i<20;i++)
	{
		NodePush(head ,i);
	}
	PrintListReverse(head);
	PrintListReverse1(head);
}

7 重建二叉树

题目：输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如，输入前序遍历序列｛1，2，4，7，3，5，6，8｝和中序遍历序列｛4，7，2，1，5，3，8，6｝，则重建二叉树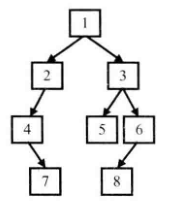
思路：二叉树的前序遍历和中序遍历就不讲了，自己看一下。其实编程就是把自己的思路用计算机去实现。所以先用语言把思路写出来：根是前序遍历的第一个，左子树是中序遍历中根的左边，右子树是中序遍历中根的右边。不断递归就好了。
结束条件：没有左子树也没有右子树。

程序写的有点蠢了，非要用指针加来加去搞复杂了，其实看成数组，用数组标会简单点。写了一般的时候发现的也就懒得改了，大家可以试试传入首地址和长度，用下标去做。

#include <stdio.h>
#include <stdlib.h>
#define bool unsigned int
#define true 1
#define false 0
#define none 2

typedef struct binaryTreeNode
{
	int value;
	struct binaryTreeNode* left;
	struct binaryTreeNode* right;
}binaryTree;

binaryTree* ConstructCore(int *inorderStart,int* inorderEnd,int *preorderStart,int* preorderEnd)
{

	int *p;
	int *preorderEndLeft;
	binaryTree* root = (binaryTree*)malloc(sizeof(binaryTree));
	if(inorderStart == inorderEnd)//结束条件
	{
		 if(*inorderEnd != *preorderEnd)return false;
		 else
		 {
			 root->left = NULL;
			 root->right = NULL;
			 root->value = *preorderStart;
			 return root;
		 }
	}
	root->value = *preorderStart++;
	for(p = inorderStart;p<=inorderEnd && *p!=root->value;p++);
	if(p>inorderEnd)return false;//中序遍历中没找到根节点
	preorderEndLeft = preorderStart+(p-1-inorderStart);
	root->left = ConstructCore(inorderStart,p-1,preorderStart,preorderEndLeft);
	root->right = ConstructCore(p+1,inorderEnd,preorderEndLeft+1,preorderEnd);
	return root;
}
binaryTree* Construct(int preorder[],int inorder[],int length1,int length2)
{
	if(length1!=length2 || !length1)
		return false;
	return ConstructCore(inorder,inorder+length1-1,preorder,preorder+length2-1);
	

}
int main()
{
	int preorder[] = {1,2,4,7,3,5,6,8};
	int inorder[] = {4,7,2,1,5,3,8,6};
	binaryTree* root = Construct(preorder,inorder,sizeof(preorder)/sizeof(int),sizeof(inorder)/sizeof(int));
}

8 二叉树的下一个节点

题目：给定一棵二叉树和其中的一个节点，如何找出中序遍历的下一个节点？树中的节点除了有两个分别指向左右子节点的指针，还有一个指向父节点的指针。

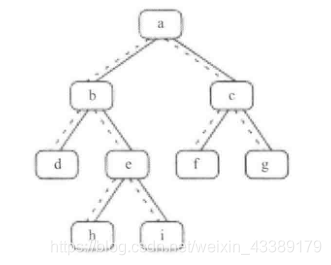
思路：先用文字理清思路：二叉树中序遍历找下一个节点。上图的中序遍历为dbheiafcg,有三种情况：
1.有右子树，那就去找右子树中最左的子树。b的下一个是h
2.没有右子树，但是是双亲的左子树。那说明它是双亲左子树里面最后一个，所以下一个就是双亲。比如d的下一个是b
3.没有右子树 ，还是双亲的右子树。那说明双亲在他前面，需要一直向上找，找到是双亲的左子树的。这个双亲就是下一个。比如i，找到e,再找到b,再找到a，满足条件了，就是a.
(写完之后发现2和3其实有相关性，都是找有左子树的双亲，2是3的特殊情况)

#include <stdio.h>
#include <stdlib.h>
#define bool unsigned int
#define true 1
#define false 0
#define none 2

typedef struct binaryTreeNode
{
	int value;
	struct binaryTreeNode* left;
	struct binaryTreeNode* right;
	struct binaryTreeNode* parent;
}binaryTree;


binaryTree* GetNext(binaryTree* node)
{
	binaryTree* parent;
	binaryTree* current;
	if(node==NULL)return NULL;
	if(node->right!=NULL)
	{
		node = node->right;
		while(node->left!=NULL)
			node = node->left;
		return node;
	}
	else if(node->parent!=NULL)
	{
		parent = node->parent;
		current = node;
		while( parent!=NULL && current!=parent->left)//反过来会出BUG，因为parent是NULL是就访问不到left了
		{
			current = parent;
			parent = parent->parent;
		}
		if(parent!=NULL)
			return parent;
		else 
			return NULL;
	}

}
/*构建二叉树*/
binaryTree* ContructBinaryTree(int value)
{
	binaryTree* node = (binaryTree*)malloc(sizeof(binaryTree));
	node->left = NULL;
	node->right = NULL;
	node->parent = NULL;
	node->value = value;
	return node;
}
void ConnectTreeNodes(binaryTree* parent, binaryTree* left, binaryTree* right)
{
    if(parent != NULL)
    {
        parent->left = left;
        parent->right = right;

        if(left != NULL)
            left->parent = parent;
        if(right != NULL)
            right->parent = parent;
    }
}

/*打印二叉树*/
void PrintTree(binaryTree* root)
{
	if(root->left!=NULL)
		PrintTree(root->left);
	printf("%d ",root->value);
	if(root->right!=NULL)
		PrintTree(root->right);
}
int main()
{
	binaryTree *node;
	binaryTree* pNode8 = ContructBinaryTree(8);
	binaryTree* pNode6 = ContructBinaryTree(6);
	binaryTree* pNode10 = ContructBinaryTree(10);
	binaryTree* pNode5 = ContructBinaryTree(5);
	binaryTree* pNode7 = ContructBinaryTree(7);
	binaryTree* pNode9 = ContructBinaryTree(9);
	binaryTree* pNode11 = ContructBinaryTree(11);

	ConnectTreeNodes(pNode8, pNode6, pNode10);
	ConnectTreeNodes(pNode6, pNode5, pNode7);
	ConnectTreeNodes(pNode10, pNode9, pNode11);

	PrintTree(pNode8);
	node = GetNext(pNode5);
	if(node)printf("\n%d",node->value);
	node = GetNext(pNode6);
	if(node)printf("\n%d",node->value);
	node = GetNext(pNode7);
	if(node)printf("\n%d",node->value);
	node = GetNext(pNode8);
	if(node)printf("\n%d",node->value);
	node = GetNext(pNode9);
	if(node)printf("\n%d",node->value);
	node = GetNext(pNode10);
	if(node)printf("\n%d",node->value);
	node = GetNext(pNode11);
	if(node)printf("\n%d",node->value);
}

9 用两个栈实现队列

题目：用两个栈实现一个队列。
思路：很简单一道题，栈是先进先出，队列是先进后出，要想让栈有队列的效果，只需要在出栈的时候再建立一个辅助栈，然后：1.先把原始栈出栈到辅助栈里面。2.从辅助栈中出栈。3.将辅助栈的东西再出栈回原栈。4.释放辅助栈
这道题如果放在C++里面分分钟就写完了，因为C++自带栈函数，但是用C语言就要自己写进栈函数、出栈函数了，代码量还有点大。还有一点就是虽然在子函数中构建栈，子函数返回后会把子函数的栈都释放的，但是栈是要单独申请空间的，不是存在子函数栈中。所以在用完的时候一定要把辅助栈给释放掉。
注意：指针相减得到的是指向类型的个数，不是地址差

#include <stdio.h>
#include <stdlib.h>
#define bool unsigned int
#define true 1
#define false 0
#define none 2
#define STACK_ININ_SIZE 20//栈初始化长度
#define STACK_INCREMENT 10//每次增长长度
typedef struct Stack
{
    int *base;
    int *top;
    int stackSize;//栈长度
}Stack;

Stack* InitStack()
{
	Stack* stack = (Stack*)malloc(sizeof(Stack));
	stack->base = (int*)malloc(sizeof(int)*STACK_ININ_SIZE);
	if(stack->base)
		stack->stackSize = STACK_ININ_SIZE;
	else
		return false;
	stack->top = stack->base;
	return stack;
}
bool DestroyStack(Stack* stack)
{
	free(stack->top);
	free(stack);
}

bool PopStack(Stack *stack,int elem)
{
	int *a;
	//if((stack->top - stack->base)/sizeof(int)==stack->stackSize)
	if((stack->top - stack->base)==stack->stackSize)//等于的时候说明已经存满 指针相减就是指针指向类型的数目
	{
		a = (int*)realloc(stack->base,(stack->stackSize+STACK_INCREMENT)*sizeof(int));
		if(!a)
			return false;
		else
		{
			stack->base = a;
			stack->top = stack->base + stack->stackSize;
			stack->stackSize += STACK_INCREMENT;
		}
	}
	*stack->top++ = elem;
	return true;
}

int PushStack(Stack* stack)
{
	if(stack->top == stack->base)
		return false;
	return *--stack->top;
}

bool AppendTail(Stack* stack,int elem)
{
	if(PopStack(stack,elem))
		return true;
	else
		return false;
}

int DeleteHead(Stack* stack1)
{
	int head;
	Stack *stack2 = InitStack();
	while(stack1->top>stack1->base)
	{
		PopStack(stack2,PushStack(stack1));
	}
	head = PushStack(stack2);
	while(stack2->top>stack2->base)
	{
		PopStack(stack1,PushStack(stack2));
	}
	DestroyStack(stack2);
	return head;
}
int main()
{
	int i=0;
	int *p;
	Stack *stack1 = InitStack();
	/*构建栈*/
	for(i=1;i<31;i++)
	{
		AppendTail(stack1,i);
	}
	for(i=0;i<30;i++)
	{
		printf("%d ",DeleteHead(stack1));
	}
}

10 斐波那契数列

题目：写一个函数，输入n,求斐波那契数列的第n项。斐波那契数列的定义如下：

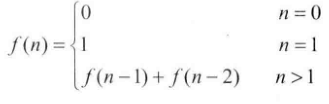
思路：
1.斐波那契是最经典的递归题目，可以用递归的方法来做。但是递归的时间复杂度和空间复杂度都很低，随着n的增大，计算量是很恐怖的。
2.用递归可以做的题目都可以用循环来做，先根据第0和1项算出第2项，再根据1和2算出第3项。需要三个变量，用来存储前两个斐波那契数。比较简单。

#include <stdio.h>
#include <stdlib.h>
#define bool unsigned int
#define true 1
#define false 0
#define none 2

int Fibonacci(unsigned int n)
{
	if(n==0)
		return 0;
	if(n==1)
		return 1;
	return Fibonacci(n-2)+Fibonacci(n-1);
	
}

int Fibonacci1(unsigned int n)
{
	int i;
	unsigned int fib1,fib2,fibN = 0;
	if(n==0)return 0;
	if(n==1)return 1;
	fib1 = 0;
	fib2 = 1;
	for(i=2;i<=n;i++)
	{
		fibN = fib1+fib2;
		fib1 = fib2;
		fib2 = fibN;
	}
	return fibN;
}
int main()
{
	int i;
	for(i=0;i<10;i++)
		printf("%d ",Fibonacci(i));
	printf("\n");
	for(i=0;i<10;i++)
		printf("%d ",Fibonacci1(i));
}

延伸题目：青蛙上楼梯问题，青蛙一次可以上一个台阶或者上两个台阶，那么问有n个台阶时，青蛙 有多少种上法。
思路：函数f(n),因为青蛙只有两个台阶选择，所以我们可以假定已经跳了一个，那么还有f(n-1)个选择；假定已经跳了两个，那么还有f(n-2)种选择。所以f(n) = f(n-1)+f(n-2).这还是斐波那契数列，只不过f(1) =1,f(2)=2.