代码随想录算法训练营day40

题目：343. 整数拆分、96.不同的二叉搜索树

参考链接：代码随想录

343. 整数拆分

思路：五部曲来走。dp数组，dp[i]用于记录拆i得到的最大乘积和，我们要求的也就是dp[n]；递推公式，我们想拆分i，可以拆成i-1和1，这样dp[i]就是dp[i-1]或者就是i-1，也可以拆成i-2和2，这样就是2dp[i-2]和2(i-2)取最大值，综合讨论一下就是拆成i-j和j，然后比较dp[i-j]*j和(i-j)*j的最大值，这里因为dp[i-j]必须要进行至少拆成两个数，所以没有包含i-j，故我们还需要比较i-j，递推公式就是dp[i]=max(dp[i-j]*j,(i-j)*j)；初始化，这里0和1根据题目无法拆分，也就无需初始化这两个，直接初始化dp[2]=1；遍历顺序和举例略。时间复杂度O(n^2)。

class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n+1);//其实这里也不用初始化为0
        dp[2]=1;
        for(int i=3;i<=n;i++){
            for(int j=1;j<=i-2;j++){//最多只能拆i-2个，这样剩下2，如果再拆得只剩1，dp[1]就没有意义了
                dp[i]=max(dp[i],max(dp[i-j]*j,(i-j)*j));//注意C++的max只能有两个参数
            }//更新dp[i]需要一个循环遍历
        }
        return dp[n];
    }
};

看标答发现可以优化，即拆分的时候拆到一半就可以了，根据数学推导，拆分成相同的子数乘积比较大，故拆得超过一半必定不可能是最大值，当然我们写代码的时候上面其实就可以了：

class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n + 1);
        dp[2] = 1;
        for (int i = 3; i <= n ; i++) {
            for (int j = 1; j <= i / 2; j++) {
                dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
            }
        }
        return dp[n];
    }
};

贪心方法需要数学证明略。

96.不同的二叉搜索树

思路：本题一看根本没有思路，主要要了解BST，就是左子树都小于头，右子树都大于头，而且每一个子树都是BST。使用dp五部曲。首先是dp[i]表示i个节点组成的不同BST个数；然后是递推公式，我们可以举例考虑3的情况和2来组合，首先是1为头结点，3可以插到1和2中间，也可以插到2右边，两种，然后是2为头节点，这时只有一种，最后是3为头结点，也是两种，共有5种。仔细对比可以发现规律，1为头时，两个节点的布局和n为2的时候一样，因为左右都是两个节点，3为头也是如此，2为头的时候，左右各一个节点，布局同n=1的情况。dp[3]就是将1,2,3分别为头结点的BST数量相加。1为头，左子树节点个数为0，右子数节点个数为2，即dp[0]*dp[2]，2为头，dp[1]*dp[1]，3为头dp[2]*dp[0]。


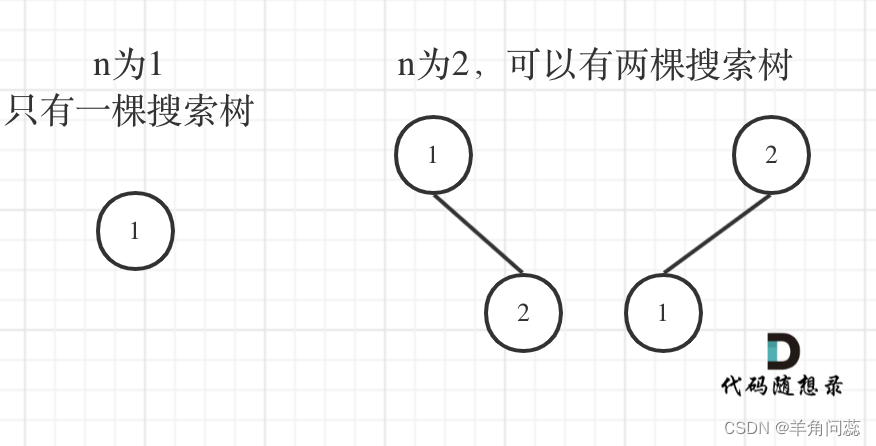
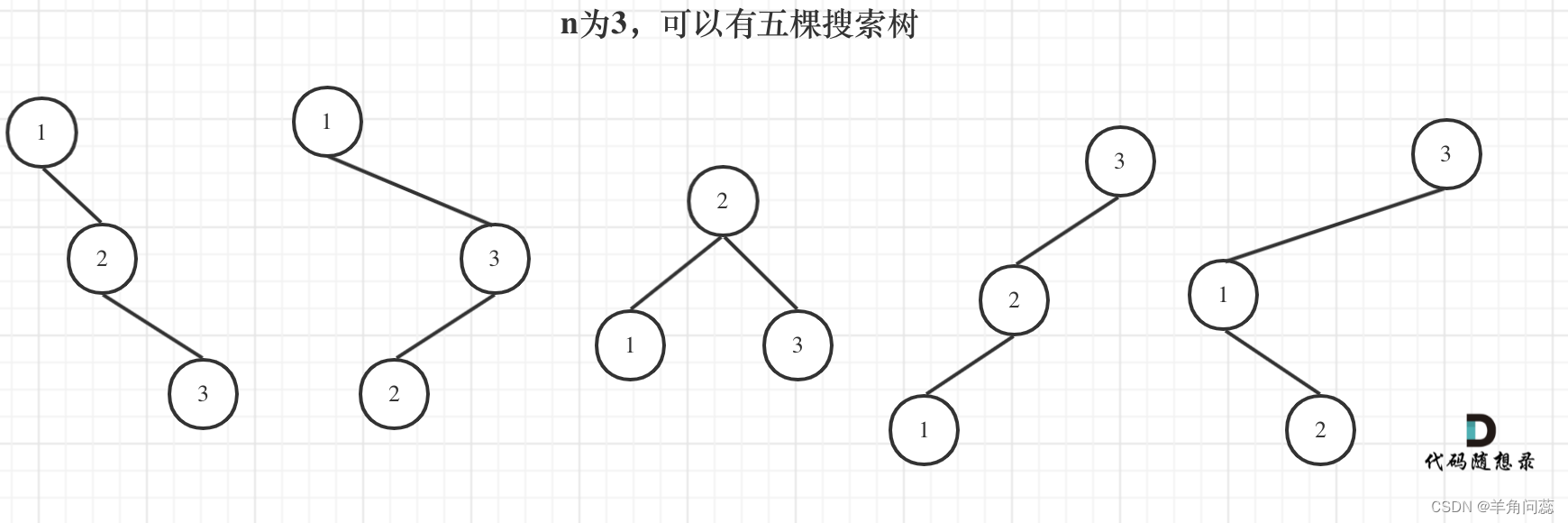
故对dp[i]，我们也考虑1到i为头节点的数量相加，dp[i]=dp[0]*dp[i-1]+dp[1]*dp[i-2]+…+dp[i-1]*dp[i]，这是重新回顾dp[i]的定义，可以定义为i个不同元素组成BST的数量；初始化，dp[0]=1，dp[1]=1，其他都可以推出来；遍历顺序从前往后；举例略。时间复杂度O(n^2)。

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n+1,0);
        dp[0]=1;
        dp[1]=1;
        for(int i=2;i<=n;i++){
            for(int j=0;j<=i-1;j++){
                dp[i]+=dp[j]*dp[i-1-j];
            }
        }
        return dp[n];
    }
};