求最短路径的3种基本方法
求最短路径的3种基本方法
情景简述：n个城市，m条道路，已知每条道路的长度。
总体思路就是：借助中间中间城市 来使得该城市相连的两个城市的路径变短。（就好比A要找C办事，但A不认识C，处理事情就相对麻烦。但A认识B， B认识C，A通过B可以轻易做成想要C做成的事情，从而减少麻烦）。
if (e[i][j] > e[i][k] + e[k][j])
{// A-i B-k C-j
e[i][j] = e[i][k] + e[k][j];
}
1.多源最短路：Floyd-Warshall
算法1.多源最短路：n个城市，m条道路，已知每条道路的长度， 求每两个个城市的最短路程。
思路：每次只允许通过 城市k（中间城市）来获得任意两城市之间的 更短路程-----最开始只允许经过1号城市进行中转，接下来允许1号和2号城市中转………允许1号-n号所有城市进行中转，从而求得任意两个城市之间的最短路程。
例如k = 1 : 即仅允许通过城市1 来缩短其他城市之间的路程。
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
{
if (e[i][j] > e[i][1] + e[1][j])
{// A-i B-1 C-j
e[i][j] = e[i][1] + e[1][j];
}
}
}
完整代码实现为：
#define _CRT_SECURE_NO_WARNINGS
#include <cstdio>
const int maxn = 1024;
const int inf = 0x3f3f3f3f;
int e[maxn][maxn];
void Init(int n)
{
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
{
e[i][j] = inf;
}
}
}
void Floyd(int n)
{
for (int k = 1; k <= n; ++k)
{
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
{
if (e[i][j] > e[i][k]+e[k][j])
{
e[i][j] = e[i][k] + e[k][j];
}
}
}
}
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
{
if (i == j) printf(j == 1 ? "0" : " 0");
else printf(j == 1 ? "%d" : " %d", e[i][j]);
}
putchar('\n');
}
}
int main()
{
int n, m;
scanf("%d %d", &n, &m); // n个结点，m条边
Init(n); // 初始化e数组
for (int i = 1; i <= m; ++i)
{
int x, y, d;
scanf("%d %d %d", &x, &y, &d);
e[x][y] = d;
}
Floyd(n); //floyd算法
return 0;
}
给出一组测试数据：
4 8
1 2 2
1 3 6
1 4 4
2 3 3
3 1 7
3 4 1
4 1 5
4 3 12
测试结果：
0 2 5 4
9 0 3 4
6 8 0 1
5 7 10 0
2.单源最短路：Dijkstra算法
2.单源最短路：n个城市，m条道路，已知每条道路的长度， 求所给城市到其他多有城市的最短路程。
思路：每次找距离源点(A)最近的城市(B)，以该城市作为中间城市进行扩展，用distance数组存储路程，book数组标记此次的中间城市是否被扩展了，该次的城市扩展完后标记，下次只在未标记的城市中找距离源点(A)最近的城市(B’, B’’, B’’’……)进行扩展，最终得到源点城市到所有城市的最短路径。
查找距离源点(A)最近的城市(B)：时间复杂度O(n);
需要进行n次查找(B) : O(n);
时间复杂度：O（n^2）;
完整代码实现为
#define _CRT_SECURE_NO_WARNINGS
#include <cstdio>
const int maxn = 1024;
const int inf = 0x3f3f3f3f;
int source, e[maxn][maxn], dis[maxn];
bool book[maxn];
void Init(int n)
{
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
{
e[i][j] = inf;
}
}
}
void Distance(int n)
{
for (int i = 1; i <= n; ++i)
{
dis[i] = e[source][i];
}
}
void Dijkstra(int n)
{
for (int i = 1; i <= n; ++i)
{// dijkstra
int mi = inf, t = -1;
for (int j = 1; j <= n; ++j)
{// 找距离源点 最小的 t
if (e[source][j] < mi && !book[j])
{
mi = e[source][j];
t = j;
}
}
if (t != -1) book[t] = 1;
for (int j = 1; j <= n; ++j)
{// 更新所有的点
if ( e[t][j] != inf && e[source][j] > e[source][t] + e[t][j])
{
e[source][j] = mi + e[t][j];
}
}
}
for (int i = 1; i <= n; ++i)
{
if (i == source) printf(i == 1 ? "0" : " 0");
else printf(i == 1 ? "%d" : " %d", e[source][i]);
}
}
int main()
{
int n, m;
scanf("%d %d", &n, &m);
scanf("%d",&source);
book[source] = 1;
Init(n); //初始化e
for (int i = 0; i < m; ++i)
{
int x, y, d;
scanf("%d %d %d", &x, &y, &d);
e[x][y] = d; //有向图
}
Distance(n); //初始化dis
Dijkstra(n); //dijkstra算法
return 0;
}
注: 若源点已经确定，可把 scanf("%d",&source); 该行代码注释掉， 在全局声明source为已知源点。
3.1解决负权边：Bellman-Ford算法
3.1带负权-单源最短路：n个城市，m条道路，已知每条道路的长度， 求源点到其他所有城市的最短路程。（计算从1号节点出发到其他任意一个节点的最短距离）
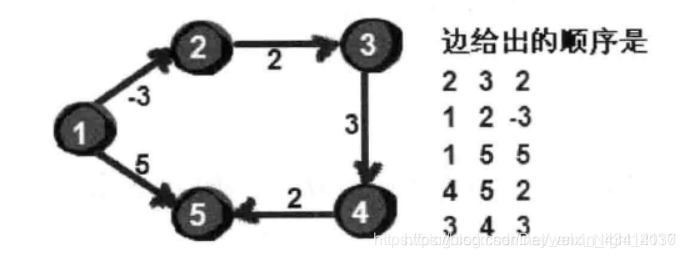
思路：用数组u，v来存储结点，对应的权值为w，每次按边进行松弛
即：
for (int i = 1; i <= m; ++i)
{
if (dis[v[i]] > dis[u[i]] + w[i])
{
dis[v[i]] = dis[u[i]] + w[i];
}
}
第一轮就是节点1 只能经过一条边 可以到达其他结点的最短路径(接着就是2-3…n-1条边) ，第二轮dis[u[i]] 就存在不是inf的距离了，依次进行（n-1）轮，即可以得到最短路径。（注：进行n-1轮松弛->若还有正权的节点,不是最短路径。->若还有负权节点,无最短路径 ）。
图片来源：https://blog.csdn.net/day_and_night_2017/article/details/96317791
完整代码实现为：
#define _CRT_SECURE_NO_WARNINGS
#include <cstdio>
const int maxn = 1024;
const int inf = 0x3f3f3f3f;
int dis[maxn], u[maxn], v[maxn], w[maxn];
// 结点存在u、v中， 对应的权值为w[i]
int main()
{
int n, m;
scanf("%d %d", &n, &m); // n个顶点，m条边
for (int i = 0; i < m; ++i)
{
scanf("%d %d %d", u+i, v+i, w+i);
}
for (int i = 1; i <= n; ++i)
{ // 初始化dis数组
dis[i] = inf;
}
dis[1] = 0; // 从结点1开始
// Bellman_Ford算法
bool check = 1; // 标记本轮数组dis是否变化
for (int k = 1; k < n && check; ++k)
{// 进行n-1轮松弛->若还有正权的节点,不是最短路径。->若还有负权节点,无最短路径
check = 0;
for (int i = 0; i < m; ++i)
{// 枚举对m条边 和输入对应 下面为v(是可能到达) -> u(已经到达)
if (dis[v[i]] > dis[u[i]] + w[i])
{
dis[v[i]] = dis[u[i]] + w[i];
check = 1;
}
}
// 第一轮就是节点1 只能经过一条边 可以到达其他结点的最短路径(接着就是2-3...n-1条边)
}
bool flag = 0; //检验是否有负权回路
for (int i = 1; i <= m; ++i)
{
if (dis[v[i]] > dis[u[i]] + w[i])
{
flag = 1;
printf("存在负权回路\n");
}
}
for (int i = 1; i <= n; ++i)
{
printf(i == 1 ? "%d" : " %d", dis[i]);
}
return 0;
}
测试数据：
5 5
2 3 2
1 2 -3
1 5 5
4 5 2
3 4 3
测试结果：
0 -3 -1 2 4
3.2Bellman-Ford的队列优化
3.2Bellman-Ford的队列优化 -实质是一个广度优先搜索：在实施每一次的松弛操作后， 会有一些顶点已经求得其最短路，此后这些顶点的dis会保持不变，不受后续松弛操作的影响，但是方法3.1还是每次都判断是否需要松弛，耗费了时间。所以每次仅对dis值发生变化的顶点进行松弛操作即可。
该小节会用到邻接表的知识： first数组存储的就是 每个顶点i (u[i]) 的按输入顺序的最后u-v边
eg：
4 5
1 4 9
4 3 8
1 2 5
2 4 6
1 3 7
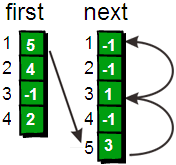
for (int i = 1; i <= m; ++i)
{// 创建邻接表
scanf("%d %d %d", u+i, v+i, w+i);
next[i] = first[u[i]];
first[u[i]] = i;
}
// 使用邻接表时：就看k = next[k], k 是否为-1来确定是否结束 eg:5->3->1->-1;
图片来源：https://blog.csdn.net/zbq_tt5/article/details/89681404（不是很清楚的可以在学习一下邻接表存储）
思路：有些结点在实施若干松弛之后，这些点的最短路的估计值就不会再变，每次判断浪费时间，所以每次仅对dis值发生变化的顶点进行松弛操作即可。
#define _CRT_SECURE_NO_WARNINGS
#include <cstdio>
#include <queue>
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 1024;
int dis[maxn],u[maxn], v[maxn], w[maxn];
int first[maxn], next[maxn];
bool book[maxn];
queue<int>que;
int main()
{
int n, m, q, p;
scanf("%d %d", &n, &m);
// 初始化dis数组 // 初始化first数组
for (int i = 1; i <= n; ++i) dis[i] = inf; dis[1] = 0;
for (int i = 1; i <= n; ++i) first[i] = -1;
for (int i = 1; i <= m; ++i)
{//first数组存储的就是 每个顶点i (u[i]) 的按输入顺序的最后u-v边
scanf("%d %d %d", u+i, v+i, w+i);
next[i] = first[u[i]];// 创建的时候先放next再放first
first[u[i]] = i;// 使用的时候先看first在用next循环
}
// Bellman-Ford的队列优化
q = 1; book[q] = true; que.push(q);//入队
while (!que.empty())
{
p = que.front(); que.pop();
int k = first[p];
while (k != -1)
{// 扫描当前结点p 所有的边
if (dis[v[k]] > dis[u[k]] + w[k])
{// 结点p 相连的所有结点 v[k]
dis[v[k]] = dis[u[k]] + w[k];
if (!book[v[k]])
{// 结点Vk未出现在队列中入队
q = v[k]; book[q] = true; que.push(q);
}
}
k = next[k];
}
book[p] = false;//可能多次入队
}
for (int i = 1; i <= n; ++i)
{
printf(i == 1 ? "%d" : " %d", dis[i]);
}
return 0;
}
测试数据同3.1一样：
5 5
2 3 2
1 2 -3
1 5 5
4 5 2
3 4 3
测试结果：
0 -3 -1 2 4
Bellman-Ford算法还有SPFA算法优化，若比较感兴趣，可自行学习。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
