模型评估指标

混淆矩阵

召回率

召回率适用于以下情况：

当我们关注的是模型能够正确找出所有真实正例的能力时，即关注模型的查全率。
在一些应用场景中，如风险预警、欺诈检测等，假阴性（FN）的代价较高，我们希望尽量减少未能正确预测为正例的情况。

精确率

精确率适用于以下情况：

当我们关注的是模型预测为正例的样本中有多少是真正的正例时，即关注模型的预测准确性。
在一些应用场景中，如量化交易预测任务，假正例（FP）的代价较高，我们希望最大限度地减少错误预测为正例的情况。

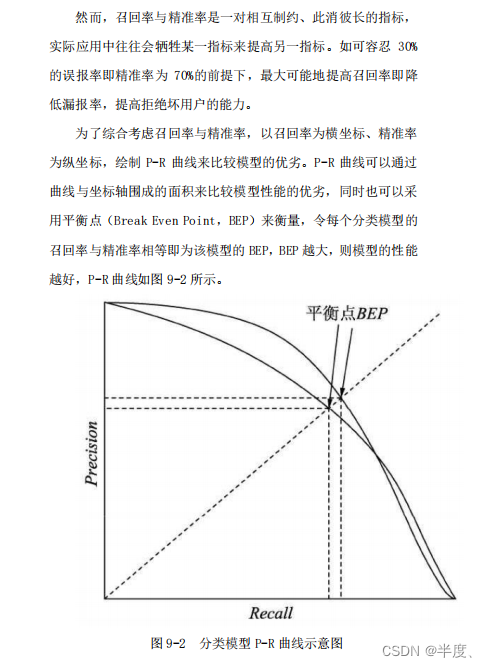
P-R曲线

F1指标

ROC曲线和AUC

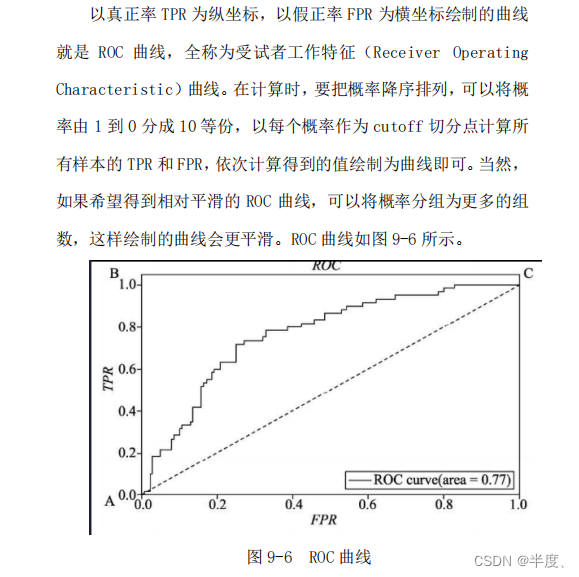
TPR（True Positive Rate）和FPR（False Positive Rate）是在二分类问题中用来衡量分类模型性能的指标。它们在业务上具有以下意义：

TPR（真正例率）也称为召回率（Recall），衡量了模型能够正确预测为正例的样本数占所有真实正例样本数的比例。在业务上，TPR可以用来评估模型的查全率，即模型能够正确找出所有真实正例的能力。例如，在医学领域中，TPR可以用来衡量模型在疾病诊断中能够正确识别出患者的能力。较高的TPR意味着模型能够更准确地找出真实正例，从而减少漏诊的风险。

FPR（假正例率）衡量了模型错误预测为正例的样本数占所有真实负例样本数的比例。在业务上，FPR可以用来评估模型的误报率，即模型将负例错误预测为正例的情况。例如，在金融领域中，FPR可以用来衡量模型在欺诈检测中将正常交易错误标记为欺诈的风险。较低的FPR意味着模型能够更准确地避免将负例错误预测为正例，从而减少误报的风险。

在实际应用中，业务场景和需求决定了对于TPR和FPR的重视程度。在一些场景中，如疾病诊断、安全检测等，较高的TPR可能更为重要，因为漏诊的代价较高。而在其他场景中，如信用评分、垃圾邮件过滤等，较低的FPR可能更为重要，因为误报的代价较高。

因此，根据具体业务需求，需要权衡和平衡TPR和FPR，选择适合的分类模型和阈值设置，以达到业务上的最优性能。

AUC优点：

• 不受类别不平衡问题影响：AUC对于类别不平衡问题具有较好的鲁棒性。它将分类模型的性能综合考虑了不同阈值下的真正例率（True Positive Rate）和假正例率（False Positive Rate），因此可以有效地评估模型在不同类别分布下的性能。
• 不受阈值选择的影响：AUC不依赖于具体的分类阈值选择，只关注正负样本的排序关系。这意味着即使在不同的阈值下，AUC也能够保持一致性。
• 直观易懂：AUC的取值范围在0到1之间，越接近1表示模型性能越好，越接近0.5表示模型性能越差。这使得AUC在解释和比较模型性能时非常直观和易懂。

缺点：

• 不适用于多类别问题：AUC通常被用于二分类问题，对于多类别问题则需要进行扩展或其他处理。在多类别问题中，AUC的解释和使用变得更加复杂。

• 对分类概率敏感：AUC是基于分类概率的排序关系来计算的，因此对于分类概率预测准确性要求较高。如果模型的概率预测不准确，AUC可能无法准确反映模型的性能。

• 无法提供具体的误差度量：AUC只是对模型整体性能的衡量，无法提供具体的误差度量。如果需要更详细的误差度量信息，可能需要使用其他指标，如准确率、召回率等。

参考书籍：金融风大数据风控建模实战