双栈排序

http://icpc.upc.edu.cn/problem.php?cid=1675&pid=3

注：此题有多种解题版本，但网上代码质量参差不齐，有待检验，对于初学者很难分辨正误，容易误入歧途，况且有些方法较为复杂，没有必要学习。因此，本文以一个初学者角度，对双栈排序进行详细解析。在此声明：本文代码已通过sicily评测, 文章内容相关引用已用带有底色方框标记。

1.Introduction
双栈排序，顾名思义，就是利用两个栈，对一串数字进行排序。但是，这种排序方式与其他排序方式有一定的差别，它并不能满足所有数串的排序。因此，对于能进行双栈排序的数串，我们称之为“可双栈排序序列”，反之，称之为“不可双栈排序序列”。

读者可以先根据“a b a a b b a b”自行尝试一下1 3 2 4的双栈排序，了解它的大致过程。 

对于本题，我采用的方法是二分图染色法。那么什么是二分图？什么是染色法？怎么构造二分图？怎么染色？这是完成这道题之前必须回答的问题，同时也是网上教程欠缺的重要内容。

2.Bipartite graph(二分图)
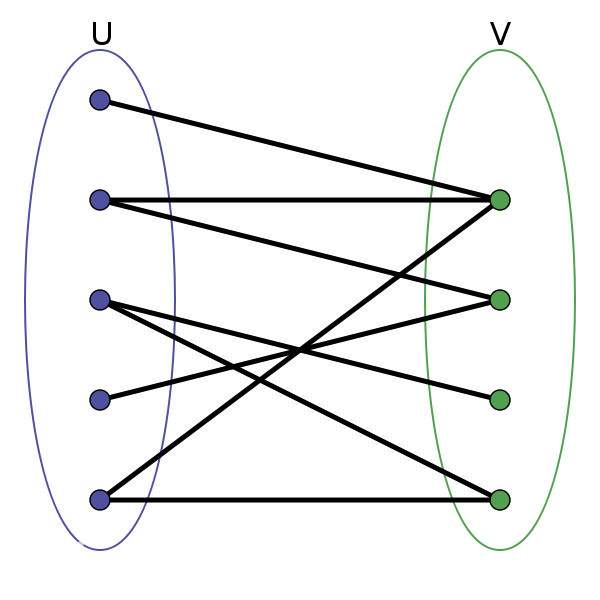
二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

对于学过离散数学的同学，就很容易理解上面这段定义了。 
G=(V, E)，其中G代表图，V代表这个图的所有顶点的集合，E代表这个图所有连线的集合，即是边集。现如今如果能将V这个顶点集分成两个互不相交的子集A、B，E这个边集内所有边的两个顶点分别属于*A、B两个子集的话，我们就称这个图为二分图*。

没有学过的同学看一下下面的这张图，再参照上面的定义，应该也能了解得差不多吧。 

了解了二分图是什么东西后，接下来我们需要了解染色这一概念。

什么是染色？就是给对象标记一种“颜色”(这里的颜色其实可以用数字定义)，其主要作用是便于分类、记，而不是实现真正意义上的染色。 
故我们可以创建一个数组，每个数组的下标对应一个元素，数组的每个元素的值代表该对象标记的颜色。如此，就完成了染色这一步骤。

而且，染色还可以用于判别一个图是否是二分图。下文会提到。

在数据结构中，我们可以通过建立二维数组(布尔矩阵) picture[MAX][MAX]来实现二分图。二维数组的横向index代表A顶点子集，纵向index代表B顶点子集(当然也可以倒过来)。如若两个顶点i, j有连接，则在对应的picture[i][j] 与 picture[j][i]处赋值为1或true。

虽然二维数组可以代表图，但并不代表每一个二维数组都是二分图。那么如何检验呢？那就要通过深度优先搜索dfs进行染色验证了。

对于深度优先搜索，我只提供相关链接，就不详细阐述了：Depth-first_search 
如果上面链接看完后还是不懂，可以自行查书或者百度相关博客进行学习。

二分图的条件：通过深度优先搜索对每个顶点进行染色，如果相邻顶点颜色相同或者是同一顶点出现染不同颜色的情况，则说明该图不是二分图。

3.Solution
（注：引用部分来自博文sicily双栈排序）

双栈排序的方法便是二分图染色法。即对数字串进行两个两个逐次遍历，如果符合规则A的便将二者连接起来，则当遍历结束后完成构图。然后通过dfs染色，确立真正的二分图。然后借助染色表(记录每个元素颜色的数组)，进行相应的push(), pop()操作，最终便能完成排序。

而这一规则A便是：

考虑对于任意两个数q[i]和q[j],它们不能压入同一个栈中的充要条件: 存在一个k,使得i<j<k且q[k]<q[i]<q[j]。

其证明过程如下：

定理：考虑对于任意两个数q[i]和q[j],它们不能压入同一个栈中的充要条件: 存在一个k,使得i<j<k且q[k]<q[i]<q[j]。

证明： 
充分性：即如果满足上述条件，那么q[i]和q[j]一定不能压入同一个栈。

证明(反证法)假设这两个数压入了同一个栈,那么压入q[k]，因为q[k]比q[i]和q[j]都小，所以很显然,当q[k]没有被弹出的时候，另两个数也都不能被弹出(否则输出序列的数字顺序就不是1,2,3,…,n了)。而之后,无论其它的数字在什么时候被弹出,q[j]总是会在q[i]之前弹出，而q[j]>q[i],这显然是不正确的.

必要性：如果两个数不可以压入同一个栈，那么它们一定满足上述条件。

证明逆否命题：也就是”如果不满足上述条件，那么这两个数一定可以压入同一个栈。”不满足上述条件有两种情况： 
情况1：对于任意i<j<k且q[i]<q[j]，q[k]>q[i]；（即对任意三个数，最小的总是在最前面） 
情况2：对于任意i<j，q[i]>q[j]。 
第一种情况：在q[k]被压入栈的时候，q[i]已经被弹出栈。那么,q[k]不会对q[j]产生任何影响(这里可能有点乱，因为看起来,q[j]<q[k]的时候是会有影响的，但实际上，这还需要另一个数r，满足j<k<r且 q[r]<q[j]<q[k],也就是证明充分性的时候所说的情况。而事实上我们现在并不考虑这个r，所以说q[k]对q[j]没有影响)。 
第二种情况：可以发现这其实就是一个降序序列，所以所有数字都可以压入同一个栈。这样，原命题的逆否命题得证，所以原命题得证。

解题步骤

(1) 检查数列中的数字是否满足进入同一个栈的条件，如果不满足则将边连上，构造二分图。 
(2) 用dfs染色，把二分图染成1和2两种颜色，使得染色为1的结点被压入s1栈，染色为2结点被压入s2栈。具体：每次选取一个未染色的编号最小的结点，将它染色为1，并从它开始dfs染色，直到所有结点都被染色为止。这样，我们就得到了每个结点应该压入哪个栈中。注意dfs结束之后未被染色的数字是可以被放入同一个栈的，所以优先染色为1。如果发现某一个数字两次要染不同的颜色，则为不能输出。

我个人的代码：

# include <iostream>
# include <stack>
// The MAX is suitable for 1001(at least), but I set it to 1003 for safe.
# define MAX 1003
using namespace std;

bool picture[MAX][MAX];   // bipartite graph
int color[MAX];  // The color of elements
int temp[MAX];  // The storage of elements that we want to sort
int small[MAX];  // An array use for judge whether the two numbers obey the rule
int num; // The number of elements we want to enter
bool flag; // Make up whether the string of number can fit into  two－stack sort

/* set_color: use dfs to set the color */
void set_color(int i, int c) {
    color[i] = c;
    for (int j = 0; j < num; j++) {
        if (picture[i][j]) {  // Find the adjacent point
            if (color[j] == c) {    // adjacent points have the same color it will be wrong
                flag = false;
            }
            if (!color[j]) {  // if the point has never be drawn, set the color of it
                set_color(j, 3-c);  // 3-c only have two result: 1, 2, represent stack1 and stack2
            }
        }
    }
}
/* Creat_Picture: create the bipartite graph with regard to the rule */
void Creat_Picture() {
    small[num] = 0x7FFFFFFF;  // INT_MAX, you can set the number that bigger than the elements you put
    for (int i = num-1; i >= 0; i--) {
        small[i] = temp[i];
        if (small[i+1] < small[i]) {   // create the array for the rule
            small[i] = small[i+1];
        }
    }
    for (int i = 0; i < num-1; i++) {
        for (int j = i+1; j < num; j++) {
            if (temp[i] < temp[j] && small[j+1] < temp[i]) {
                picture[i][j] = picture[j][i] = 1;    // create the gragh according to the rule
            }
        }
    }
    for (int i = 0; i < num; i++) {
        if (!color[i]) {       // set the default color to 1 for the unsigned one
            set_color(i, 1);
        }
    }
}

void Calculate() {
    if (flag == false) {
        cout << "0" << endl;
        return;
    }
    stack<int> stack1;  // store the element that has color one
    stack<int> stack2; // store the element that has color two
    int count = 0; // Use for judging whether we should add the space
    int aim = 1; // Use for judging whether we should pop the element
    for (int i = 0; i < num; i++) {
        if (color[i] == 1) {
            stack1.push(temp[i]);
            count++;
            cout << "a";
            if (count < num*2) {
                cout << " ";
            }
        } else {
            stack2.push(temp[i]);
            count++;
            cout << "c";
            if (count < num*2) {
                cout << " ";
            }
        }
        // while-loop is important, we should pop the element after we push the element
        while ((!stack1.empty() && stack1.top() == aim) ||
               (!stack2.empty() && stack2.top() == aim)) {
            if (!stack1.empty() && stack1.top() == aim) {
                stack1.pop();
                count++;
                aim++;
                cout << "b";
                if (count < num*2) {
                    cout << " ";
                }
            } else {
                stack2.pop();
                count++;
                aim++;
                cout << "d";
                if (count < num*2) {
                    cout << " ";
                }
            }
        }
    }
    cout << endl;
}

int main(void) {
    while(cin >> num) {
        flag = true;
        for (int i = 0; i < MAX; i++) {
            color[i] = 0;
            temp[i] = 0;
            small[i] = 0;
            for (int j = 0; j < MAX; j++) {
                picture[i][j] = 0;
            }
        }
        for (int i = 0; i < num; i++) {
            cin >> temp[i];
        }
        Creat_Picture();
        Calculate();
    }
    return 0;
}

大家可以结合我的博客内容和代码了解双栈排序。可能单看内容比较难理解，所以推荐结合起来看。由于我代码中有较为详细的注释，这里就不多说了。

下面看到代码中while循环：

        while ((!stack1.empty() && stack1.top() == aim) ||
               (!stack2.empty() && stack2.top() == aim)) {
            if (!stack1.empty() && stack1.top() == aim) {
                stack1.pop();
                count++;
                aim++;
                cout << "b";
                if (count < num*2) {
                    cout << " ";
                }
            } else {
                stack2.pop();
                count++;
                aim++;
                cout << "d";
                if (count < num*2) {
                    cout << " ";
                }
            }
        }

本题有一种错误的思路便是每次压栈前将栈顶元素与要压入的元素比较，如若栈顶大，则正常插入；如果栈顶小，则先弹出栈顶，直至栈顶大于压入元素或者栈顶为空时再压入。这种思路会导致得不到字典序最小的字符串。假如我栈1可以弹出元素，而你下一步是压栈2，那么你的操作可能是ca，但显然此处ac也是合理的，且字典序更小。所以正确的思路便是在每一次压栈后进行弹出操作。

当时我回看这段代码时，总感觉有点不对劲。因为题目要求输出的是字典序最小的操作。假如有这种情况：我下一个元素压栈1，但在这之前根据while循环是将栈1栈2所有能弹出的部分都弹出。如果我先弹出栈1中能弹出的内容，然后在压栈1，再弹出栈2中可以弹出的内容，那么岂不是能构成字典序更小的字符串？但我多方尝试，也没有找到能符合这种情况的数据。也许该算法避免了这种情况的发生，即这种情况在这个算法下是不可能事件。所以我觉得可能是我多虑了。

4.Conclusion
这道双栈排序涉及到了二分图的构造与检验，染色法，深度优先搜索，数据结构等知识，含金量非常高，自己感觉收获颇丰，有兴趣的同学推荐学习！

分析条件，我们把问题抽象为数学模型。设输入序列为S，考虑S[i],S[j]两个元素不能进入同一个栈的条件.注意,这里所说的"S[i],S[j]两个元素不能进入同一个栈",不是说仅仅不能同时在一个栈中,而是自始至终不能进入一个栈,即如果有解,那么S[i],S[j]一定进入过的栈不同.

结论P: S[i],S[j]两个元素不能进入同一个栈 <=> 存在k,满足i<j<k,使得S[k]<S[i]<S[j]. 证明略过,请参考sqybi.尝试后可以发现结论P是正确的.

把每个元素按照输入序列中的顺序编号,看作一个图中的每个顶点.这时,我们对所有的(i,j)满足i<j,判断是否满足结论P,即S[i],S[j]两个元素能否进入同一个栈.如果满足P,则在i,j之间连接一条边.

我们对图染色,由于只有两个栈,我们得到的图必须是二分图才能满足条件.由于要求字典序最小,即尽量要进入栈1,我们按编号递增的顺序从每个未染色的顶点开始染色,相邻的顶点染上不同的色,如果发生冲突,则是无解的.否则我们可以得到每个顶点颜色,即应该进入的栈.

接下来就是输出序列了,知道了每个元素的决策,直接模拟了.

在判断数对(i,j)是否满足P时,枚举检查是否存在k的时间复杂度是O(n),则总的时间复杂度是O(n^3),对于n=1000是太大了.这原因在于过多得枚举了k,我们可以用动态规划把枚举k变为O(1)的算法.

设F[i]为Min{S[i],S[i+1],S[i+2]..S[n-1],S[n]},状态转移方程为F[i]=Min{ S[i] , F[i+1] }.边界为F[N+1]=极大的值.

判断数对(i,j)是否满足P,只需判断(S[i]<S[j] 并且 F[j+1]<S[i])即可.时间复杂度为O(n^2).

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <stack>
using namespace std;
const int maxn = 1000+5;
bool Edge[maxn][maxn];
int s[maxn],F[maxn], color[maxn];
stack<int> staA,staB;
int n;
void  NoAnswer()
{
      printf("0\n"); 
      exit(0);
}
void  dfs(int x, int c)
{
      color[x] = c;
      for (int i = 1; i <= n; ++i)
      if (Edge[x][i])
      {
          if (color[i] == c ) NoAnswer();
          if (!color[i])
             dfs(i, 3-c);
      }
}
int main()
{
    cin>>n;
    for ( int  i = 1 ;  i <= n ; ++i) cin>>s[i];
    F[n+1] = 0x7fffffff;
    for (int i = n; i>=1; --i) F[i] = min(s[i], F[i+1]);
    
    
    for (int i = 1; i < n  ; ++i)
        for (int j = i+1; j <=n ;++j)
        if (s[i] < s[j] && F[j+1]<s[i])
           Edge[i][j] = Edge[j][i] = true;
           
    for (int i = 1; i <= n;++i)
        if ( !color[i]) dfs(i,1);
        
        
    int aim = 1;
    for (int i = 1; i <= n; ++i)
    {
        if (color[i]==1)
        {
           staA.push(s[i]);
           printf("a ");
        } else
        {
           staB.push(s[i]);
           printf("c ");
        }
        
        while (!staA.empty() && staA.top() == aim || 
               !staB.empty() && staB.top()== aim)
        {
              if (!staA.empty() && staA.top()== aim)
              {
                  staA.pop();
                  printf("b ");
              } else
              {
                  staB.pop();
                  printf("d ");
              }
              aim ++;
        }
    }
    return 0;
}

解析：
       就算知道是二分图染色还是不会TT。

       首先考虑怎么判断是否有解。

       a [ i ] 和 a [ j ] 不能压入同一个栈（在同一个栈中出现过）⇔ 存在一个k,使得 i < j < k 且 a [ k ] < a [ i ] < a [ j ]

       严格证明就比较复杂了，我就说如何感性理解吧（反正在考场上也没几个人会去严格证明）。

       因为一个数只能进出一次，k 要排在前面所以弹出 k 时 i 和 j 都在栈里，如果两者在同一个栈弹出后顺序就错误了，然后找不到除这种情况外的反例，于是就这样了。。。

       所以如果输入数据不能使得所有限制成立则无解，然后就可以转化成二分图染色来判定，不能在同一个栈中就连边。

       关于输出答案，因为要让字典序最小肯定是尽量加在S1里面，实在不行加进S2。

 

代码：

#include <bits/stdc++.h>
using namespace std;
 
const int Max=1010;
int n,m=1,size,tot1,tot2,p1[Max],p2[Max];
int first[Max],f[Max],num[Max],vis[Max];
struct shu{int to,next,len;}edge[Max*Max];
 

inline void build(int x,int y)
{
    edge[++size].next=first[x],first[x]=size,edge[size].to=y;
    edge[++size].next=first[y],first[y]=size,edge[size].to=x;
}
 
inline void pre()
{
    f[n]=num[n];
    for(int i=n-1;i>=1;i--) f[i]=min(f[i+1],num[i]);
    for(int i=1;i<=n;i++)
      for(int j=i+1;j<=n;j++)
        if(f[j]<num[i]&&num[i]<num[j]) build(i,j);
}
 
inline bool dfs(int p,int color)
{
    vis[p]=color;
    for(int u=first[p];u;u=edge[u].next)
    {
      int to=edge[u].to;
      if(!vis[to]) dfs(to,3-color);
      else if(color==vis[to]) return 0;
    }
    return 1;
}
 
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&num[i]);
    pre();
    for(int i=1;i<=n;i++) if(!vis[i]&&!dfs(i,1)) {puts("0");return 0;}
    for(int i=1;i<=n;i++)
    {
      if(vis[i]==1)p1[++tot1]=num[i],printf("a ");
      else p2[++tot2]=num[i],printf("c ");
      while(m==p1[tot1]||m==p2[tot2])
      {
          if(m==p1[tot1]) tot1--,printf("b ");
          else tot2--,printf("d ");
          m++;
      }
    }
    return 0;

1.先考虑单栈情况：
    定理：考虑对于任意两个数q[i]和q[j],它们不能压入同一个栈中的充要条件: 存在一个k,使得i<j<k且q[k]<q[i]<q[j]。
    证明：
        充分性：即如果满足上述条件，那么q[i]和q[j]一定不能压入同一个栈。

            反证法:假设这两个数压入了同一个栈,那么压入q[k]，因为q[k]比q[i]和q[j]都小，所以很显然,当q[k]没有被弹出的时候，另两个数也都不能被弹出(否则输出序列的数字顺序就不是1,2,3,…,n了)。而之后,无论其它的数字在什么时候被弹出,q[j]总是会在q[i]之前弹出，而q[j]>q[i],这显然是不正确的.
        必要性：如果两个数不可以压入同一个栈，那么它们一定满足上述条件。
            证明逆否命题：也就是"如果不满足上述条件，那么这两个数一定可以压入同一个栈。”不满足上述条件有两种情况：
                情况1：对于任意i<j<k且q[i]<q[j]，q[k]>q[i]；（即对任意三个数，最小的总是在最前面）
                情况2：对于任意i<j，q[i]>q[j]。
                第一种情况：在q[k]被压入栈的时候，q[i]已经被弹出栈。那么,q[k]不会对q[j]产生任何影响(这里可能有点乱，因为看起来,q[j]<q[k]的时候是会有影响的，但实际上，这还需要另一个数r，满足j<k<r且 q[r]<q[j]<q[k],也就是证明充分性的时候所说的情况。而事实上我们现在并不考虑这个r，所以说q[k]对q[j]没有影响)。
            第二种情况：可以发现这其实就是一个降序序列，所以所有数字都可以压入同一个栈。这样，原命题的逆否命题得证，所以原命题得证。

2. 双栈情况：
2.1 判断是否有解和任意两个数能否压入同一个栈
(1) 对任意两个数q[i]和q[j],若存在一个k,使得i<j<k且q[k]<q[i]<q[j]，则这两个数分别入s1栈和s2栈

(2) 将s1栈和s2栈中的数字分成两个顶点子集，同一顶点子集内不会出现任何连边，即不能压入同一个栈的所有数字被分到了两个栈中。任意两个不在同一栈的数字间连边。此时我们只考虑检查是否有解，所以只要花O(n)时间检查这个图是不是二分图,就可以得知是否有解了。

*（二分图是一种特殊类型的图：图中的顶点集被划分成X与Y两个子集,图中每条边的两个端点一定是一个属于X而另一个属于Y。二分图的匹配是求边的一个子集，该子集中的任意两条边都没有公共的端点。）

2.2 解题步骤：

(1) 检查数列中的数字是否满足进入同一个栈的条件，如果不满足则将边连上，构造二分图。

(2) 用dfs染色，把二分图染成1和2两种颜色，使得染色为1的结点被压入s1栈，染色为2结点被压入s2栈。具体：每次选取一个未染色的编号最小的结点，将它染色为1，并从它开始dfs染色，直到所有结点都被染色为止。这样，我们就得到了每个结点应该压入哪个栈中。注意dfs结束之后未被染色的数字是可以被放入同一个栈的，所以优先染色为1。如果发现某一个数字两次要染不同的颜色，则为不能输出。

(3) 模拟出栈操作。

3.特殊情况与注意点：
3.1 为了判断是否满足同一个栈的条件，需要对数组进行预先处理，得到一个记录每一位数字之后最小数字的数列。

3.2 模拟输出的时候，考虑这样一种情况：此时将栈1排空了，可以压入数字，也可以继续输出栈2的数字。如果模拟的时候直接顺序排列a, b, c, d四种操作，则b结束后，因为预先染色不能压入c，则进行d操作了。这是不对的，因为需要先压入栈1，再排出栈2，顺序应该是a d而不是d a。从这个角度来说，找到的很多代码其实是错误的。需要增加一个循环元素，如果排空栈1之后可以压入则回到循环顶部先压入s1在去输出栈2的数字。
代码

#include <iostream>
#include <cmath>
#include <stack>
#include <string>
using namespace std;
 
// global
bool edges[1005][1005]; // if there is edges between pos i and pos j num
int color[1005]; // color of each num, 0 initial, 1 color A, 2 color B
bool can_output; // if can be sort
 
// put color on num using dfs
void dfs(int keyPos, int color_, int n) {
  color[keyPos] = color_;
  for (int i = 0; i < n; i++) {
    if (edges[keyPos][i]) {
      if (color[i] == color_) {
        can_output = false;
        break;
      } else if (!color[i]) {
        dfs(i, 3 - color_, n);
      }
    }
    if (edges[i][keyPos]) {
      if (color[i] == color_) {
        can_output = false;
        break;
      } else if (!color[i]) {
        dfs(i, 3 - color_, n);
      }
    }
  }
}
 
int main () {
  int n;
  int num[1005];
  int postMin[1005]; // smallest num behind each pos
  while (cin >> n) {
    // initialize
    for (int i = 0; i < 1005; i++) {
      color[i] = 0;
      for (int j = 0; j < 1005; j++) {
        edges[i][j] = false;
      }
    }
    can_output = true;
    // input
    for (int i = 0; i < n; i++) {
      cin >> num[i];
    }
    // compute postMin
    for (int i = n - 1; i >= 0; i--) {
      if (i == n - 1) {
        postMin[i] = num[i];
      } else {
        postMin[i] = min(num[i], postMin[i + 1]);
      }
    }
    // make edges
    //int count = 0;
    for (int i = 0; i < n - 1; i++) {
      for (int j = i + 1; j < n; j++) {
        if (num[i] < num[j] && postMin[j] < num[i]) {
          // cannot be put into same stack;
          edges[i][j] = edges[j][i] = true;
          //count++;
        }
      }
    }
    //cout << "Edges: " << count << endl;
    // color the num
    for (int i = 0; i < n; i++) {
      if (!color[i]) {
        dfs(i, 1, n);
      }
    }
 
    // output
    // cout << "Start output" << endl;
    stack<int> s1, s2;
    string order;
    if (can_output) {
      // simulate output
      // cout << "Start simulation" << endl;
      int output_num = 1; // the num to be output
      int pos = 0; // the pos of the numbers
      // no edge between two num means they can be put into one stack
      while (output_num <= n) {
        if (color[pos] == 1) {
          order += "a";
          s1.push(num[pos++]);
          // cout << "Push: " << num[pos - 1] << " a" << endl;
        }
        while (!s1.empty() && s1.top() == output_num) {
          // cout << "Pop: " << s1.top() << " b" << endl;
          s1.pop();
          order += "b";
          output_num++;
        }
        if (color[pos] == 1 && (s1.empty() || s1.top() > num[pos])) {
          continue;
        }
        while (!s2.empty() && s2.top() == output_num) {
          // cout << "Pop: " << s2.top() << " d" << endl;
          s2.pop();
          order += "d";
          output_num++;
        }
        if (color[pos] == 2) {
          order += "c";
          s2.push(num[pos++]);
          // cout << "Push: " << num[pos - 1] << " c" << endl;
        }
      }
      for (int i = 0; i < order.length(); i++) {
        if (i) {
          cout << " ";
        }
        cout << order[i];
      }
      cout << endl;
    } else {
      cout << "0" << endl;
    }
 
    while (!s1.empty()) {
      s1.pop();
    }
    while (!s2.empty()) {
      s2.pop();
    }
    order.clear();
  }
 
 
  return 0;