1.允许空盒
问题描述
n个相同的小球,放入m个相同的盒子里,允许有空盒,问有多少种不同的方法?
解题思路
f(i,k) 表示把 i 个相同的小球放入 k 个相同的盒子中且允许有空盒的放法数。
(1) 把 i 个小球放入到 k 个盒子中,如果盒子数 k 比小球数i还要多,那么一定有空的盒子,这时只考虑 i 个盒子即可。
(2) 若盒子数不超过小球数,则对方法进行分类,分成两类:有盒子为空的放法和没盒子为空的放法。
(2.1) 有盒子为空的放法:先拿走一个盒子,把 i 个小球放入 k - 1 个盒子中,有f(i,k-1) 种放法。
(2.2) 没盒子为空的放法:先从 i 个小球中拿出 k 个,每个盒子先放一个,这样 k 个盒子中至少有 k 个小球了,剩下的 i - k 个小球,再放到 k 个盒子中,有**f(i-k, k)**种放法。
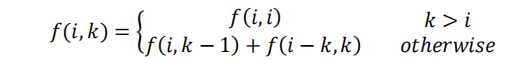
边界条件
5个小球放入1个盒子,显然只有一种放法,f(5, 1) = f(5, 0) + f(4, 1)。f(4, 1)也显然为1,于是f(5, 0)应该就是0。同样我们也可以分析出发f(1, 0) = 0。
1个小球放入1个盒子中,f(1, 1) = f(1, 0) + f(0, 1),而f(0, 1)等于f(0, 0),它们都等于1。
代码
#include<iostream>
using namespace std;
int f(int i, int j)
{
if(i < j)
return f(i, i);
if(i == 0)
return 1; //特别注意这两个出口条件的顺序,要是先判断k == 0就返回0.这样就错了
if(j == 0)
return 0;
return f(i, j - 1) + f(i - j, j);
}
int main()
{
int i, j;
cin >> i >> j;
cout << f(i, j) << endl;
return 0;
}
2.不允许空盒
问题描述
n个相同的小球,放入m个相同的盒子里,不允许有空盒,问有多少种不同的方法?
解题思路
step表示当前剩余的小球需要分成的盒子数
把n分成k份,只需第⼀个盒子中小球数等于i,计算从i等于1⼀直到i等于n/k,然后把剩余的n-i分成k-1份的种类数…
pre为前一个小盒中的球数,每次i从pre开始⼀直到n/step结束,这样才能保证每个小盒中的小球数是不递减的,才能保证不会有重复的情况产⽣
代码
#include <iostream>
using namespace std;
int cnt = 0;
void dfs(int pre, int n, int step)
{
if(step == 1) {
cnt++;
return;
}
for(int i = pre; i <= n / step; i++)
dfs(i, n - i, step - 1);
}
int main() {
int n, k;
cin >> n >> k;
dfs(1, n, k);
cout << cnt << endl;
return 0;
}






















 2554
2554











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








