（算法）对斐波拉契数列的算法思考

对斐波拉契数列的思考

美其名曰是我自己的思考？实际也是老生常谈了。。自己走一遍过遍手，可能会有点不同的印象吧
都知道斐波拉契数列有一种经典解法：

public class Feibo{
    public static void main(String[] args) {
    long begintime=System.nanoTime();
    int n=50;
    System.out.print(count(n));
    long endtime = System.nanoTime();
    long costTime = (endtime - begintime)/1000;
        //要换算为微秒，就除上1000，就可以
    System.out.println("代码用时："+costTime+"ms"); 
    }
    static long count(int n){
       if(n==1)return 1;
       if(n==2)return 1;
       return count(n-1)+count(n-2);
    }
}

嘤嘤嘤算一个加到50算了我将近一分钟

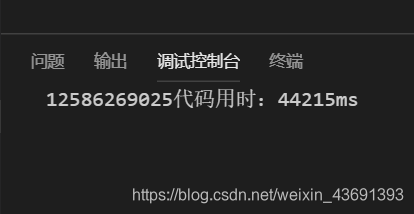
整个思路很自然，每一个都是前面两个数的和，我们把问题化为更普遍更小的问题之后递归就是了
当然，从上面的计算时间也可以看出来，确确实实耗时有点长，所以我们试着对程序优化
整个递归的结构还是一个二叉树的结构。

可以看到，递归算法中，count（3）被调用了两次，count(2)被调用了三次
我们自然而然的想到，用空间换时间即在每次计算后我们将其储存起来，之后只需要检索而不需要再次递归了。
这就是动态规划法的初级版本

public class Feibo{
    public static void main(String[] args) {
    long begintime=System.nanoTime();
    
    int n=50;
    long[] storage;
    storage=new long[n+1];
    for(int i=1;i<=n;i++)storage[i]=0;
    System.out.print(count(n,storage));

    long endtime = System.nanoTime();
    long costTime = (endtime - begintime)/1000;
    System.out.println("代码用时："+costTime+"微秒"); 
    }
    static long count(int n,long[]storage){
        
        if(n==1)return 1;
        if(n==2)return 1;
        if(storage[n]!=0)return storage[n];
        return storage[n]=count(n-1,storage)+count(n-2,storage);
    }
  
}

这样输出结果：

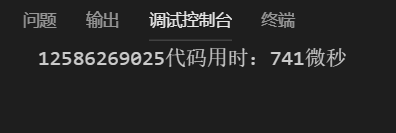
都是用的微秒级别了。问题来了，时间复杂度是多少？我觉得是O(n)吧

动态规划的本质核心问题在于确定状态和状态转移。说白了，就是一个阶段的解可以由前一个阶段的解得到。而我储存前一个阶段的解，就是在“动态规划”
更加简单的说，动态规划具备以下三个特点：

1. 把原来的问题分解成了三个相似的子问题（强调“相似子问题”）
2. 所有的子问题都只需要解决一次（强调“只解决一次”）
   3. 储存子问题的解。（强调“储存”）

归根结底，概念并不重要，如果用自底而上的思考方式，会得到非递归的算法。
子问题即只关心前面两个数的值，我们可以简单的算每两个数然后储存即可

public class Feibo{
    public static void main(String[] args) {
    long begintime=System.nanoTime();
    
    int n=50;
    long[] storage;
    storage=new long[n+1];
    for(int i=1;i<=n;i++)storage[i]=0;
   // System.out.print(count(n,storage));
    System.out.println(Add(n, storage));

    long endtime = System.nanoTime();
    long costTime = (endtime - begintime)/1000;
    System.out.println("代码用时："+costTime+"微秒"); 
    }
   static long Add(int n,long[] storage){
        storage[1]=storage[2]=1;
        for(int i=3;i<=n;i++){
            storage[i]=storage[i-1]+storage[i-2];
        }
        return storage[n];
    }
}

时间复杂度也是O(n)，

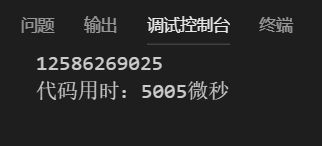
其实这才是斐波拉契最自然的解法，也是应该一开始想到的解法（有其是以前没学过递推的时候）
更深刻的看问题，递归解法是一种自顶向下，循环解法是一种自底向上
为了更好的理解动态规划，我又去做了下动态规划里的“Hello World”——最长上升子序列问题

public class LIS{
    public static void main(String arg[]){

    long begintime = System.nanoTime();
	//代码部分
    int[] arr={1,2,6,-3,6,1,3,4,2,-1,-5,46,39,30,-31,6,40,-7,9,11,23,8,-3,-4,-2,33,-7,-22,87,23,11,120,0,15};
     //int[] arr={2,5,3,4,1,7,6};
    System.out.println(LIS_Solve(arr));
    //计时部分    
    long endtime = System.nanoTime();
    long costTime = (endtime - begintime)/1000;
       
    System.out.println("代码用时："+costTime+"微秒");   
    }
    public static int  LIS_Solve(int[] arr) {
        //对于每一个集合，arr[0~i]的最长上升子序列等于arr[0~i-1]最长上升子序列+1吗？明显不一定
        //但是这样的思考让我们意识到了，实际上每个最长上升子序列的最关键标志在于其最后一个数啊
        //所以我们有这样的想法:以arr[i]结尾的最长上升子序列长度等于以arr[0~i-1]中的i个数arr[j]中
        //if(arr[j]<arr[i]&&len[j]+1>=len[i]) len[i]=len[j]+1（len[i]是以arr[i]结尾的上升子序长度）
        int res=0;//res用来装最长长度
        int[] len;
        len=new int[arr.length];
        for(int i=0;i<arr.length;i++){
            len[i]=1;
            for(int j=0;j<i;j++){
                if(arr[j]<arr[i]&&len[j]+1>=len[i])
                len[i]=len[j]+1;
            }
            if(len[i]>res)res=len[i];
            
        }
        return res;
    }
}    

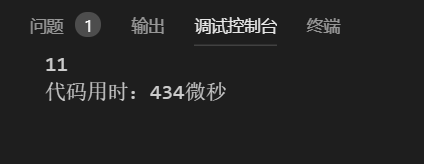
效率还行哈哈
这是自底向上方法，我觉得自然有自顶向下的方式，明天想想