搜索与图论
目录
DFS
排列数字
1.dfs进行递归,表示的意义?
此题中dfs表示的含义是:求出从第u行到最后一行的所有path。
2.如何加深对dfs的理解(求法)?
dfs的求法:根据通项公式的含义,假设已知第u+1行到最后一行的所有path,综合1和2得出:path[u] 与 path[u+1] 合并后,即为dfs的解。
3.为何回溯时,进行现场的恢复?
回溯的特征是:递归的最外层是一个循环。因为一次dfs得到的是所有的path。每一次都是从当前现场中去取得剩下未访问的元素。(这一块自己画个图就很容易理解)。
反证:如果不进行现场的恢复,则在第一次完成深搜后,所有元素都已经被访问过了。这样在回溯到上一层时,上层的现场中的状态都被下层更改了,数据就会乱套。
#include <iostream>
using namespace std;
const int N = 10;
int path[N];
bool st[N];
int n;
// 计算u->n的所经过的路径path
void dfs(int u)
{
// 边界条件
if (u == n)
{
for (int i = 0; i < n; i++) printf("%d ", path[i]);
puts("");
return;
}
else
{
for (int i = 1; i <= n; i++)
{
if (!st[i])
{
path[u] = i;
st[i] = true;
dfs(u+1); // 回溯之后,为何要恢复现场?
path[u] = 0;
st[i] = false;
}
}
}
}
int main()
{
scanf("%d", &n);
dfs(0);
return 0;
}
n皇后问题
算法一:
思路
下面的(x,y)相当于(u,i)
(1)反对角线 y=x+b,截距b=y−x,因为我们要把b当做数组下标,所以 b 不能是负的,所以我们 +n,保证是结果是正的
(2)而对角线 y=−x+b,截距是 b=y+x这里截距一定是正的,所以不需要加偏移量
核心目的:找一些合法的下标来表示dg或udg是否被标记过,所以如果你愿意,你取 udg[n+n−u+i]也可以,只要所有(u,i)对可以映射过去就行。
#include <iostream>
using namespace std;
const int N = 20;
// bool数组用来判断搜索的下一个位置是否可行
// col列,dg对角线,udg反对角线
// g[N][N]用来存路径
int n;
char g[N][N];
bool col[N], dg[N], udg[N];
void dfs(int u) {
// u == n 表示已经搜了n行,故输出这条路径
if (u == n) {
for (int i = 0; i < n; i ++ ) puts(g[i]); // 等价于cout << g[i] << endl;
puts(""); // 换行
return;
}
//对n个位置按行搜索
for (int i = 0; i < n; i ++ )
// 剪枝(对于不满足要求的点,不再继续往下搜索)
// udg[n - u + i],+n是为了保证下标非负
if (!col[i] && !dg[u + i] && !udg[n - u + i]) {
g[u][i] = 'Q';
col[i] = dg[u + i] = udg[n - u + i] = true;
dfs(u + 1);
col[i] = dg[u + i] = udg[n - u + i] = false; // 恢复现场 这步很关键
g[u][i] = '.';
}
}
int main() {
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
g[i][j] = '.';
dfs(0);
return 0;
}
算法二:
// 不同搜索顺序 时间复杂度不同 所以搜索顺序很重要!
#include <iostream>
using namespace std;
const int N = 20;
int n;
char g[N][N];
bool row[N], col[N], dg[N], udg[N]; // 因为是一个个搜索,所以加了row
// s表示已经放上去的皇后个数
void dfs(int x, int y, int s)
{
// 处理超出边界的情况
if (y == n) y = 0, x ++ ;
if (x == n) { // x==n说明已经枚举完n^2个位置了
if (s == n) { // s==n说明成功放上去了n个皇后
for (int i = 0; i < n; i ++ ) puts(g[i]);
puts("");
}
return;
}
// 分支1:放皇后
if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n]) {
g[x][y] = 'Q';
row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
dfs(x, y + 1, s + 1);
row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;
g[x][y] = '.';
}
// 分支2:不放皇后
dfs(x, y + 1, s);
}
int main() {
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
g[i][j] = '.';
dfs(0, 0, 0);
return 0;
}
BFS
走迷宫
边路权值为1
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e2 + 7;
int g[N][N], d[N][N];
int n, m;
int bfs() {
int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};
queue <PII> q;
for (auto &v : d)
for (auto &x : v) {
x = - 1;
}
d[0][0] = 0;
q.push({0, 0});
while (!q.empty()) {
auto t = q.front();
q.pop();
for (int i = 0; i < 4; i++) {
int x = t.first + dx[i], y = t.second + dy[i];
if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1) {
d[x][y] = d[t.first][t.second] + 1;
q.push({x, y});
}
}
}
return d[n - 1][m - 1];
}
int main() {
cin >> n >> m;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> g[i][j];
}
}
cout << bfs() << endl;
return 0;
}
边路权值为2
#include<stdio.h>
#include<queue>
#include<iostream>
using namespace std;
char maze[201][201];
int sx, sy, tx, ty;
//左右上下4个方向
int dx[4] = { 1,0,-1,0 };
int dy[4] = { 0,1,0,-1 };
int m, n;
struct node {
int x, y, dis;
};
bool operator < (const node & a, const node & b) {
return a.dis > b.dis;
}
void bfs() {
priority_queue<node> que;
node st { sx,sy,0 };
maze[sx][sy] = '#';
que.push(st);
while (!que.empty()) {
node p = que.top();
que.pop();
//若已找到,则退出
if (p.x == tx && p.y == ty) {
cout << p.dis << endl;
return;
}
for (int i = 0; i < 4; ++i) {
int nx = p.x + dx[i];
int ny = p.y + dy[i];
node np{ nx,ny, 0};
if (nx >= 0 && nx < n&&ny >= 0 && ny < m&&maze[nx][ny] != '#') {
if (maze[nx][ny] == 'X')
np.dis = p.dis + 2;
else
np.dis = p.dis + 1;
maze[np.x][np.y] = '#';
que.push(np);
}
}
}
printf("impossible\n");
}
int main() {
while (cin>>n>>m) {
for (int i = 0; i < n; i++)
scanf("%s", maze[i]);
for(int i=0; i<n; i++)
for (int j = 0; j < m; j++) {
if (maze[i][j] == 'S')
sx = i, sy = j;
else if (maze[i][j] == 'T')
tx = i, ty = j;
}
bfs();
}
return 0;
}
八数码
算法1
(手写hash)
注:蓝桥杯可使用map(有序)函数,但此题测试用例会超时
#include<cstring>
#include<iostream>
#include<queue>
using namespace std;
int fact[9];
bool vis[362880];
int permutation_hash(char s[]) //求长度为9的字符串某种排列的哈希值
{
int ans = 0;
for(int i = 0; i < 9; i ++)
{
int d = 0;
for(int j = 0; j < i; j ++)
if(s[j] > s[i]) d ++; //求s[i]与其前面的字符组成的逆序对个数
ans += d * fact[i];
}
return ans;
}
typedef struct{
char s[10];
int step;
int k; //'x'在第k位
}Point;
int dx[4] = {-1, 0, 1, 0};
int dy[4] = { 0,-1, 0, 1};
int bfs(Point p)
{
vis[permutation_hash(p.s)] = true;
queue<Point> q;
q.push(p);
while(!q.empty())
{
p = q.front();
q.pop();
/*
printf("%d ",p.step); //print调试法
puts(p.s);
*/
if(!strcmp(p.s , "12345678x")) return p.step;
int x = p.k / 3; //'x'的行数
int y = p.k % 3; //'x'的列数
Point next;
next.step = p.step + 1;
for(int i = 0; i < 4; i ++)
{
int nx = x + dx[i];
int ny = y + dy[i];
if(nx >= 0 && nx <= 2 && ny >= 0 && ny <= 2)
{
next.k = nx * 3 + ny; //求出'x'在字符串中的的新位置
strcpy(next.s, p.s);
next.s[9] = 0;
next.s[p.k] = p.s[next.k]; //先用即将和'x'交换的字符覆盖'x'之前的位置
next.s[next.k] = 'x'; //再给'x'的新位置赋值'x'
int hash = permutation_hash(next.s);
if(!vis[hash])
{
vis[hash] = true;
q.push(next);
}
}
}
}
return -1;
}
int main()
{
fact[0] = 1;
for(int i = 1; i < 9; i ++) fact[i] = fact[i - 1] * i; //预处理fact[i] = i!
char c[2],str[10];
Point start;
for(int i = 0; i < 9; i ++)
{
scanf("%s",&c);
if(c[0] == 'x') start.k = i;
start.s[i] = c[0];
}
start.s[9] = 0;
start.step = 0;
printf("%d",bfs(start));
return 0;
}
算法2
(用unordered_map函数)
#include<bits/stdc++.h>
using namespace std;
//该结点是将二维数组状态压缩成一个字符串
int bfs(string state)
{
queue<string>q;//队列存放节点
unordered_map<string,int>d;
//存放到达该结点的最短步数(d[string]的值)
q.push(state); //节点入队
d[state]=0;//到达该结点的步数为零步
string end="12345678x";
int dx[4]={0,0,-1,1};
int dy[4]={1,-1,0,0};
//遍历当前状态下该结点上下左右四个方向
while(q.size())//队列中有节点
{
string t=q.front();//临时变量t等于队列中的头结点
q.pop();//出队
if(t==end)return d[t];
//找到答案,返回最短路径
int distance=d[t];
//临时变量distance存放到达当前节点的最短路径
/*为什么需要distance临时变量?
因为下面改变字符串后,字符串t更新,找不到该状态下的上一个状态*/
int k=t.find('x');
//找到可变换节点的坐标
int x=k/3,y=k%3;
//转换为二维,为了寻找其上下左右四个节点
for(int i=0;i<4;i++)
{
int a=x+dx[i];
int b=y+dy[i];
if(a>=0&&a<3&&b>=0&&b<3)
{
swap(t[a*3+b],t[k]);
//在一维中将符合条件的节点和可变换节点进行位置交换
if(!d.count(t))
{
d[t]=distance+1;
q.push(t);
}
swap(t[a*3+b],t[k]);
//字符串恢复到原来,继续遍历下种状态是否可行
}
}
}
return -1;
}
int main()
{
string state;
char c;
for(int i=0;i<9;i++)
{
cin>>c;
state+=c;
}
cout << bfs(state) << endl;
return 0;
}
树和图的深度优先遍历
树的重心
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e5 + 10; //数据范围是10的5次方
const int M = 2 * N; //以有向图的格式存储无向图,所以每个节点至多对应2n-2条边
int h[N]; //邻接表存储树,有n个节点,所以需要n个队列头节点
int e[M]; //存储元素
int ne[M]; //存储列表的next值
int idx; //单链表指针
int n; //题目所给的输入,n个节点
int ans = N; //表示重心的所有的子树中,最大的子树的结点数目
bool st[N]; //记录节点是否被访问过,访问过则标记为true
//a所对应的单链表中插入b a作为根
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// dfs 框架
/*
void dfs(int u){
st[u]=true; // 标记一下,记录为已经被搜索过了,下面进行搜索过程
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
if(!st[j]) {
dfs(j);
}
}
}
*/
//返回以u为根的子树中节点的个数,包括u节点
int dfs(int u) {
int res = 0; //存储 删掉某个节点之后,最大的连通子图节点数
st[u] = true; //标记访问过u节点
int sum = 1; //存储 以u为根的树 的节点数, 包括u,如图中的4号节点
//访问u的每个子节点
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
//因为每个节点的编号都是不一样的,所以 用编号为下标 来标记是否被访问过
if (!st[j]) {
int s = dfs(j); // u节点的单棵子树节点数 如图中的size值
res = max(res, s); // 记录最大联通子图的节点数
sum += s; //以j为根的树 的节点数
}
}
//n-sum 如图中的n-size值,不包括根节点4;
res = max(res, n - sum); // 选择u节点为重心,最大的 连通子图节点数
ans = min(res, ans); //遍历过的假设重心中,最小的最大联通子图的 节点数
return sum;
}
int main() {
memset(h, -1, sizeof h); //初始化h数组 -1表示尾节点
cin >> n; //表示树的结点数
// 题目接下来会输入,n-1行数据,
// 树中是不存在环的,对于有n个节点的树,必定是n-1条边
for (int i = 0; i < n - 1; i++) {
int a, b;
cin >> a >> b;
add(a, b), add(b, a); //无向图
}
dfs(1); //可以任意选定一个节点开始 u<=n
cout << ans << endl;
return 0;
}
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e5+10;
//用链表结构存储每个点的边
int h[N]; //h[]用于存储每个点的头节点
int e[2*N]; //用于存储元素 因为是无向图 所以是双向边 应该乘2
int ne[2*N]; //存储链表的next值
int idx=0;
int n;
int ans=N; //记录重心子树的最小值
bool st[N]; //记录该点是否已经查找过
void add(int a,int b) //将b插入a中 a作为根 所以处在链表的最后
{
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
int dfs(int u) //dfs过程寻找根的连通的点
{
int size=0; //存放连通块中点的个数的最大值
st[u]=true; // 该点已经走过
int sum=0; //sum用于记录根子树的个数
for(int i=h[u];i!=-1;i=ne[i])
{
int j=e[i];
if(!st[j])
{
int s=dfs(j);
size=max(size,s);
sum+=s;
}
}
size=max(size,n-sum-1); //通过画图可得n-m 即总的节点-根的子树 即为剩余的连通节点值
//而size为当前为根的子树的个数 通过比较确认连通块中点的最大数
ans=min(ans,size);
return sum+1; //return sum+1 是因为sum初始化为0 而当前这个点即根也算是该连通块内的一点
}
int main()
{
memset(h,-1,sizeof h); //初始化h[]表 -1表示空
scanf("%d",&n);
for(int i=0;i<n-1;i++) //注意这里应该n-1,
{ //有些奇怪但是 仔细想想就明白 n是表示点的个数 而每行是输入两个点之间的边所以只需输入n-1行即可
int a,b;
scanf("%d%d",&a,&b);
add(a,b);
add(b,a);
}
dfs(1);
cout<<ans<<endl;
return 0;
}
树与图的广度优先遍历
图中点的层次
#include <cstring>
#include <iostream>
using namespace std;
const int N=1e5+10;
int h[N], e[N], idx, ne[N];
int d[N]; //存储每个节点离起点的距离 d[1]=0
int n, m; //n个节点m条边
int q[N]; //存储层次遍历序列 0号节点是编号为1的节点
void add(int a, int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int bfs()
{
int hh=0,tt=0;
q[0]=1; //0号节点是编号为1的节点
memset(d,-1,sizeof d);
d[1]=0; //存储每个节点离起点的距离
//当我们的队列不为空时
while(hh<=tt)
{
//取出队列头部节点
int t=q[hh++];
//遍历t节点的每一个邻边
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
//如果j没有被扩展过
if(d[j]==-1)
{
d[j]=d[t]+1; //d[j]存储j节点离起点的距离,并标记为访问过
q[++tt] = j; //把j结点 压入队列
}
}
}
return d[n];
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof h);
for(int i=0;i<m;i++)
{
int a,b;
cin>>a>>b;
add(a,b);
}
cout<<bfs()<<endl;
}
拓扑排序
有向图的拓扑序列
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e5 + 10;
int e[N],ne[N],h[N],idx,d[N],n,m,top[N],cnt = 1;
// e,ne,h,idx 邻接表模板
// d 代表每个元素的入度
// top是拓扑排序的序列,cnt代表top中有多少个元素
void add(int a,int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx ++;
}
bool topsort(){
queue<int> q;
int t;
for(int i = 1;i <= n; ++i)// 将所有入度为0的点加入队列
if(d[i] == 0) q.push(i);
while(q.size()){
t = q.front();//每次取出队列的首部
top[cnt] = t;//加入到 拓扑序列中
cnt ++; // 序列中的元素 ++
q.pop();
for(int i = h[t];i != -1; i = ne[i]){
// 遍历 t 点的出边
int j = e[i];
d[j] --;// j 的入度 --
if(d[j] == 0) q.push(j); //如果 j 入度为0,加入队列当中
}
}
if(cnt < n) return 0;
else return 1;
}
int main(){
int a,b;
cin >> n >> m;
memset(h,-1,sizeof h);
while(m--){
cin >> a >> b;
add(a,b);
d[b] ++;// a -> b , b的入度++
}
if(topsort() == 0) cout << "-1";
else {
for(int i = 1;i <= n; ++i){
cout << top[i] <<" ";
}
}
return 0;
}
最短路问题

Dijkstra
Dijkstra求最短路径I
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=510;
int g[N][N]; //为稠密阵所以用邻接矩阵存储
int dist[N]; //用于记录每一个点距离第一个点的距离
bool st[N]; //用于记录该点的最短距离是否已经确定
int n,m;
int Dijkstra()
{
memset(dist, 0x3f,sizeof dist); //初始化距离 0x3f代表无限大
dist[1]=0; //第一个点到自身的距离为0
for(int i=0;i<n;i++) //有n个点所以要进行n次 迭代
{
int t=-1; //t存储当前访问的点
for(int j=1;j<=n;j++) //这里的j代表的是从1号点开始
if(!st[j]&&(t==-1||dist[t]>dist[j]))
t=j;
st[t]=true;
for(int j=1;j<=n;j++) //依次更新每个点所到相邻的点路径值
dist[j]=min(dist[j],dist[t]+g[t][j]);
}
if(dist[n]==0x3f3f3f3f) return -1; //如果第n个点路径为无穷大即不存在最低路径
return dist[n];
}
int main()
{
cin>>n>>m;
memset(g,0x3f,sizeof g); //初始化图 因为是求最短路径
//所以每个点初始为无限大
while(m--)
{
int x,y,z;
cin>>x>>y>>z;
g[x][y]=min(g[x][y],z); //如果发生重边的情况则保留最短的一条边
}
cout<<Dijkstra()<<endl;
return 0;
}
Dijkstra求最短路径II
朴素的算法O(n^2)
for (int i = 0; i < n; i++) {
int t = -1;
for (int j = 1; j <= n; j++) {
if (!st[j] && (t == -1 || dist[j] < dist[t]))
t = j; // O(n) * O(n) -> O(n^2)
}
st[t] = true; // O(n) * O(1) -> O(n)
for (int j = 1; j <= n; j++) {
dist[j] = min(dist[j], dist[t] + g[t][j]); //O(n) * O(n) -> O(n^2)
}
}
堆优化(mlog(n))
//遍历大部分的边
while (heap.size()) {
auto t = heap.top(); //O(m) * O(1) -> O(m)
heap.pop();
int ver = t.second, distance = t.first;
if (st[ver])continue;
st[ver] = true; //O(m) * O(1) -> O(m)
for (int i = h[ver]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] > distance + w[i]) {
dist[j] = distance + w[i];
heap.push({dist[j], j});
// 堆的插入操作时间复杂度是 O(log(n))
// O(m) * O(log(n)) -> O(mlog(n))
}
}
}
区别
稠密图使用邻接矩阵存储
稀疏图使用邻接表存储
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef pair<int, int> PII; //<离起点的距离, 节点编号>
const int N = 150010;
int h[N], e[N], ne[N], idx, w[N];
int dist[N];
bool st[N];
int n, m;
//在a节点之后插入一个b节点,权重为c
void add(int a, int b, int c) {
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
int dijkstra() {
// 所有距离初始化为无穷大
memset(dist, 0x3f, sizeof dist);
// 1号节点距离为0
dist[1] = 0;
// 建立一个小根堆
priority_queue<PII, vector<PII>, greater<PII>> heap;
// 1号节点插入堆
heap.push({0, 1});
while (heap.size()) {
// 取出堆顶顶点
auto t = heap.top();
// 并删除
heap.pop();
// 取出节点编号和节点距离
int ver = t.second, distance = t.first;
// 如果节点被访问过,则跳过
if (st[ver])continue;
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i]) {
// 取出节点编号
int j = e[i];
// dist[j] 大于从t过来的距离
if (dist[j] > distance + w[i]) {
dist[j] = distance + w[i];
heap.push({dist[j], j});
}
}
}
if (dist[n] == 0x3f3f3f3f)return -1;
return dist[n];
}
int main() {
memset(h, -1, sizeof h);
cin >> n >> m;
while (m--) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
}
cout << dijkstra() << endl;
return 0;
}
bellman ——ford
有边数限制的最短路
#include <algorithm>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 510, M = 10010;
struct Edge
{
int a, b, c;
} edges[M];
int n, m, k;
int dist[N];
int last[N];
void bellman_ford()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < k; i++) {
memcpy(last, dist, sizeof dist); //只用上一次迭代的结果
for (int j = 0; j < m; j++) {
auto e = edges[j];
dist[e.b] = min(dist[e.b], last[e.a] + e.c);
}
}
}
int main()
{
cin >> n >> m >> k;
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
edges[i] = {a, b, c};
}
bellman_ford();
if (dist[n] > 0x3f3f3f3f / 2) {
cout << "impossible" << endl;
}
else {
cout << dist[n] << endl;
}
return 0;
}
spfa
spfa求最短路
分析
终于来到SPFA算法了!之前已经说明过了Bellman_ford算法 ,我们今天说明的SPFA算法仅仅只是对该算法的一个优化。
Bellman_ford算法会遍历所有的边,但是有很多的边遍历了其实没有什么意义,我们只用遍历那些到源点距离变小的点所连接的边即可,只有当一个点的前驱结点更新了,该节点才会得到更新;因此考虑到这一点,我们将创建一个队列每一次加入距离被更新的结点。
值得注意的是
- st数组的作用:判断当前的点是否已经加入到队列当中了;已经加入队列的结点就不需要反复的把该点加入到队列中了,就算此次还是会更新到源点的距离,那只用更新一下数值而不用加入到队列当中。
即便不使用st数组最终也没有什么关系,但是使用的好处在于可以提升效率。 - SPFA算法看上去和Dijstra算法长得有一些像但是其中的意义还是相差甚远的:
1] Dijkstra算法中的st数组保存的是当前确定了到源点距离最小的点,且一旦确定了最小那么就不可逆了(不可标记为true后改变为false);SPFA算法中的st数组仅仅只是表示的当前发生过更新的点,且spfa中的st数组可逆(可以在标记为true之后又标记为false)。顺带一提的是BFS中的st数组记录的是当前已经被遍历过的点。
2] Dijkstra算法里使用的是优先队列保存的是当前未确定最小距离的点,目的是快速的取出当前到源点距离最小的点;SPFA算法中使用的是队列(你也可以使用别的数据结构),目的只是记录一下当前发生过更新的点。
-
⭐️Bellman_ford算法里最后return-1的判断条件写的是dist[n]>0x3f3f3f3f/2;而spfa算法写的是dist[n]==0x3f3f3f3f;其原因在于Bellman_ford算法会遍历所有的边,因此不管是不是和源点连通的边它都会得到更新;但是SPFA算法不一样,它相当于采用了BFS,因此遍历到的结点都是与源点连通的,因此如果你要求的n和源点不连通,它不会得到更新,还是保持的0x3f3f3f3f。
-
⭐️ Bellman_ford算法可以存在负权回路,是因为其循环的次数是有限制的因此最终不会发生死循环;但是SPFA算法不可以,由于用了队列来存储,只要发生了更新就会不断的入队,因此假如有负权回路请你不要用SPFA否则会死循环。
-
⭐️由于SPFA算法是由Bellman_ford算法优化而来,在最坏的情况下时间复杂度和它一样即时间复杂度为 O(nm)O(nm) ,假如题目时间允许可以直接用SPFA算法去解Dijkstra算法的题目。(好像SPFA有点小小万能的感觉?)
-
⭐️求负环一般使用SPFA算法,方法是用一个cnt数组记录每个点到源点的边数,一个点被更新一次就+1,一旦有点的边数达到了n那就证明存在了负环。
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N=1e5+10;
#define fi first
#define se second
typedef pair<int,int> PII;//到源点的距离,下标号
int h[N],e[N],w[N],ne[N],idx=0;
int dist[N];//各点到源点的距离
bool st[N];
int n,m;
void add(int a,int b,int c){
e[idx]=b;w[idx]=c;ne[idx]=h[a];h[a]=idx++;
}
int spfa(){
queue<PII> q;
memset(dist,0x3f,sizeof dist);
dist[1]=0;
q.push({0,1});
st[1]=true;
while(q.size()){
PII p=q.front();
q.pop();
int t=p.se;
st[t]=false;//从队列中取出来之后该节点st被标记为false,代表之后该节点如果发生更新可再次入队
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(dist[j]>dist[t]+w[i]){
dist[j]=dist[t]+w[i];
if(!st[j]){//当前已经加入队列的结点,无需再次加入队列,即便发生了更新也只用更新数值即可,重复添加降低效率
st[j]=true;
q.push({dist[j],j});
}
}
}
}
if(dist[n]==0x3f3f3f3f) return -1;
else return dist[n];
}
int main(){
scanf("%d%d",&n,&m);
memset(h,-1,sizeof h);
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
int res=spfa();
if(res==-1) puts("impossible");
else printf("%d",res);
return 0;
}
spfa判断负环
注意
需要从每个点都出发一次,才能完全确定此图中是否有环
cnt[j]=n 编号编号为j的节点是第n个加入路径的节点,
负环:环路之和为负, 求最短路的时候会不断在负环路打转。
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 1e5 + 10;
int h[N], e[N], w[N], ne[N], idx;
int n, m;
queue<int> q;
int st[N], dist[N], cnt[N];
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
int spfa() {
memset(dist, 0x3f, sizeof dist);
for (int i = 1; i <= n; i++) {
q.push(i);
st[i] = true;
}
st[1] = true;
while (q.size()) {
int t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] > dist[t] + w[i]) {
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
// 如果超过了n-1
// 根据抽屉原理,说明经过某个节点两次,则说明有环
if (cnt[j] >= n) return true;
if (!st[j]) {
st[j] = true;
q.push(j);
}
}
}
}
return false;
}
int main() {
memset(h, -1, sizeof h);
cin >> n >> m;
for (int i = 0; i < m; i++) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
if (spfa()) puts("Yes");
else puts("No");
}
Floyd
Floyd求最短路径
#include <iostream>
using namespace std;
const int N = 210, M = 2e+10, INF = 1e9;
int n, m, k, x, y, z;
int d[N][N];
void floyd() {
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
int main() {
cin >> n >> m >> k;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
if(i == j) d[i][j] = 0;
else d[i][j] = INF;
while(m--) {
cin >> x >> y >> z;
d[x][y] = min(d[x][y], z);
//注意保存最小的边
}
floyd();
while(k--) {
cin >> x >> y;
if(d[x][y] > INF/2) puts("impossible");
//由于有负权边存在所以约大过INF/2也很合理
else cout << d[x][y] << endl;
}
return 0;
}
Prim
Prim求最小生成树
/*
S:当前已经在联通块中的所有点的集合
1. dist[i] = inf
2. for n 次
t<-S外离S最近的点
利用t更新S外点到S的距离
st[t] = true
n次迭代之后所有点都已加入到S中
联系:Dijkstra算法是更新到起始点的距离,Prim是更新到集合S的距离
*/
#include <iostream>
#include <cstring>
using namespace std;
const int N = 510, INF = 0x3f3f3f3f;
int n, m;
int g[N][N], dist[N];
//邻接矩阵存储所有边
//dist存储其他点到S的距离
bool st[N];
int prim() {
//如果图不连通返回INF, 否则返回res
memset(dist, INF, sizeof dist);
int res = 0;
for(int i = 0; i < n; i++) {
int t = -1;
for(int j = 1; j <= n; j++)
if(!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
//寻找离集合S最近的点
if(i && dist[t] == INF) return INF;
//判断是否连通,有无最小生成树
if(i) res += dist[t];
//cout << i << ' ' << res << endl;
st[t] = true;
//更新最新S的权值和
for(int j = 1; j <= n; j++) dist[j] = min(dist[j], g[t][j]);
}
return res;
}
int main() {
cin >> n >> m;
int u, v, w;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
if(i ==j) g[i][j] = 0;
else g[i][j] = INF;
while(m--) {
cin >> u >> v >> w;
g[u][v] = g[v][u] = min(g[u][v], w);
}
int t = prim();
//临时存储防止执行两次函数导致最后仅返回0
if(t == INF) puts("impossible");
else cout << t << endl;
}
Kruskal
kruskal算法求最小生成树
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=200010,M=100010;
int p[M];
int n,m;
struct Edge
{
int a,b,w;
bool operator< (const Edge &W)const
{
return w < W.w;
}
}edges[N];
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]);
else return x;
}
int Kruskal()
{
int res=0,cnt=0;//res记录最小生成树的树边权重之和,cnt记录的是全部加入到树的集合中边的数量(可能有多个集合)
for(int i=0;i<m;i++)
{
int a=edges[i].a,b=edges[i].b,w=edges[i].w;
if(find(a)!=find(b))
/*
具体可以参考连通块中点的数量,如果a和b已经在一个集合当中了,说明这两个点已经被一种方式连接起来了,
如果加入a-b这条边,会导致集合中有环的生成,而树中不允许有环生成,所以一个连通块中的点的数量假设
为x,那么里面x个节点应该是被串联起来的,有x-1条边,所以只有当a,b所属的集合不同时,才能将a-b这条
边加入到总集合当中去
*/
{
p[find(a)]=p[find(b)];//将a,b所在的两个集合连接起来
cnt++;//因为加入的是a-b的这一条边,将a,b所在的两个集合连接之后,全部集合中的边数加1
res+=w;//加入到集合中的边的权重之和
}
}
if(cnt==n-1) return res;//可以生成最小生成树
else return 0x3f3f3f3f;//树中有n个节点便有n-1条边,如果cnt不等于n-1的话,说明无法生成有n个节点的树
}
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++) p[i]=i;//初始化并查集
for(int i=0;i<m;i++)
{
int a,b,w;
scanf("%d%d%d",&a,&b,&w);
edges[i]={a,b,w};
}
sort(edges,edges+m);//将边的权重按照大小一一排序
int t=Kruskal();
if(t==0x3f3f3f3f) printf("impossible\n");
else printf("%d\n",t);
return 0;
}
染色法判定二分图
染色法判断二分图
染色法
将所有点分成两个集合,使得所有边只出现在集合之间,就是二分图
二分图:一定不含有奇数环,可能包含长度为偶数的环, 不一定是连通图
dfs版本
代码思路:
染色可以使用1和2区分不同颜色,用0表示未染色
遍历所有点,每次将未染色的点进行dfs, 默认染成1或者2
由于某个点染色成功不代表整个图就是二分图,因此只有某个点染色失败才能立刻break/return
染色失败相当于存在相邻的2个点染了相同的颜色
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e5 + 10, M = 2e5 + 10; // 无向图, 所以最大边数是2倍
int e[M], ne[M], h[N], idx;
int st[N];
void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
bool dfs(int u, int color) {
st[u] = color;
for(int i = h[u]; i != -1; i = ne[i]){
int j = e[i];
if(!st[j]) {
if(!dfs(j, 3 - color)) return false;
}else if(st[j] == color) return false;
}
return true;
}
int main(){
int n, m;
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
while (m --){
int a, b;
scanf("%d%d", &a, &b);
add(a, b), add(b,a); // 无向图
}
bool flag = true;
for(int i = 1; i <= n; i ++){
if(!st[i]){
if(!dfs(i, 1)){
flag = false;
break;
}
}
}
if(flag) puts("Yes");
else puts("No");
return 0;
}
bfs版本
代码思路
颜色 1 和 2 表示不同颜色, 0 表示 未染色
定义queue是存PII,表示 <点编号, 颜色>,
同理,遍历所有点, 将未染色的点都进行bfs
队列初始化将第i个点入队, 默认颜色可以是1或2
while (队列不空)
每次获取队头t, 并遍历队头t的所有邻边
若邻边的点未染色则染上与队头t相反的颜色,并添加到队列
若邻边的点已经染色且与队头t的颜色相同, 则返回false
C++ 代码
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e5 + 10, M = 2e5 + 10;
typedef pair<int, int> PII;
int e[M], ne[M], h[N], idx;
int n, m;
int st[N];
void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
bool bfs(int u){
int hh = 0, tt = 0;
PII q[N];
q[0] = {u, 1};
st[u] = 1;
while(hh <= tt){
auto t = q[hh ++];
int ver = t.first, c = t.second;
for (int i = h[ver]; i != -1; i = ne[i]){
int j = e[i];
if(!st[j])
{
st[j] = 3 - c;
q[++ tt] = {j, 3 - c};
}
else if(st[j] == c) return false;
}
}
return true;
}
int main(){
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
while(m --){
int a, b;
scanf("%d%d", &a, &b);
add(a, b), add(b, a); // 无向图
}
int flag = true;
for(int i = 1; i <= n; i ++) {
if (!st[i]){
if(!bfs(i)){
flag = false;
break;
}
}
}
if (flag) puts("Yes");
else puts("No");
return 0;
}
匈牙利算法
二分图的最大匹配
导读:什么是最大匹配?
要了解匈牙利算法必须先理解下面的概念:
匹配:在图论中,一个「匹配」是一个边的集合,其中任意两条边都没有公共顶点。
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。
下面是一些补充概念:
完美匹配:如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。
交替路:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。
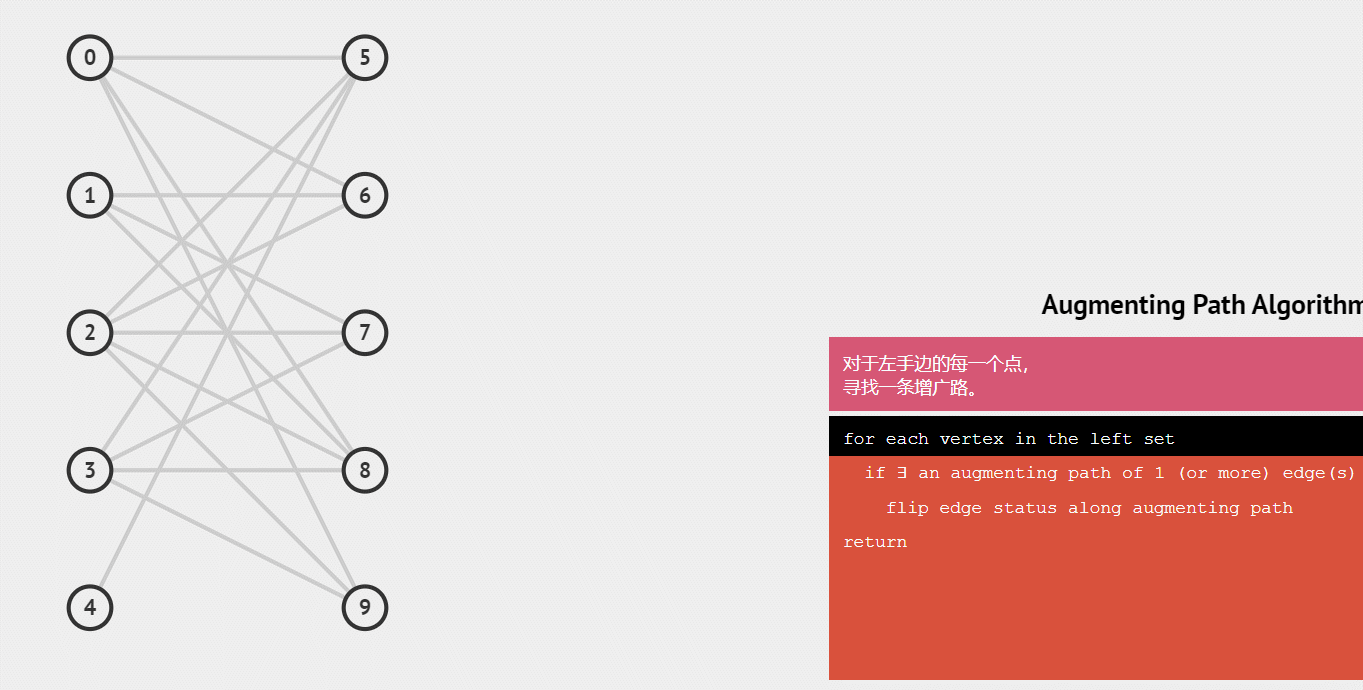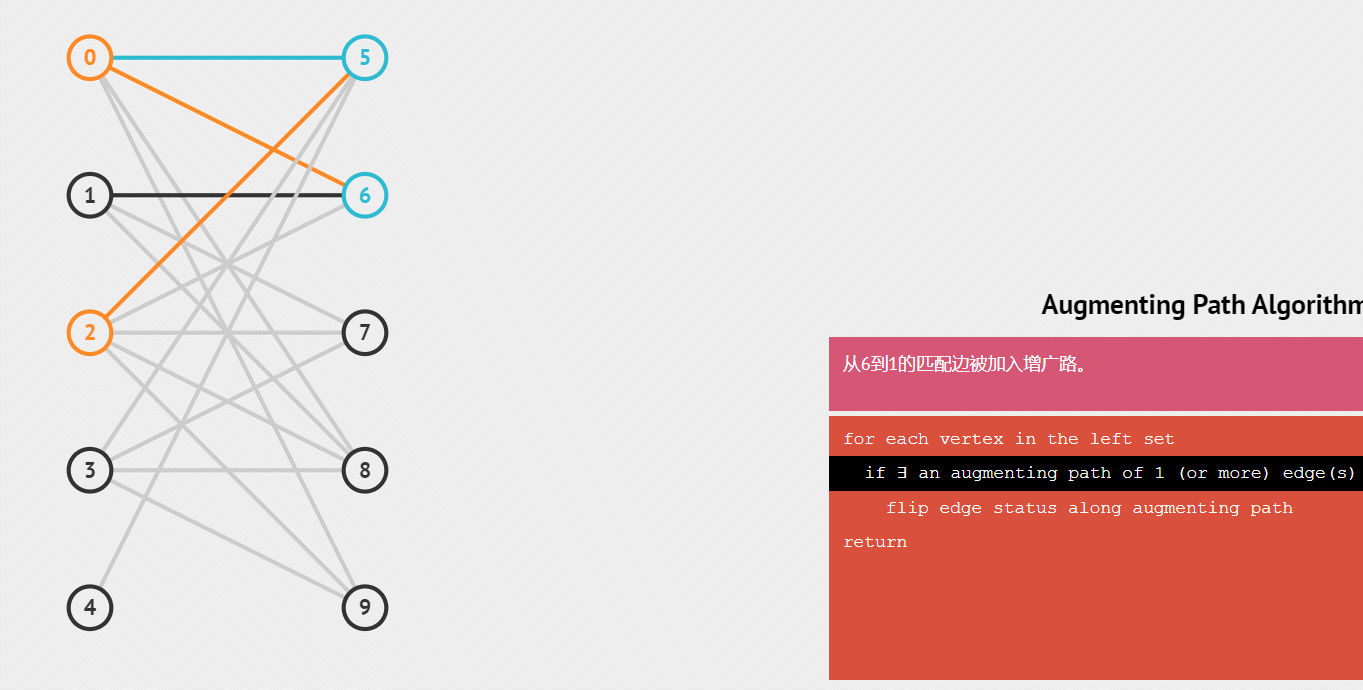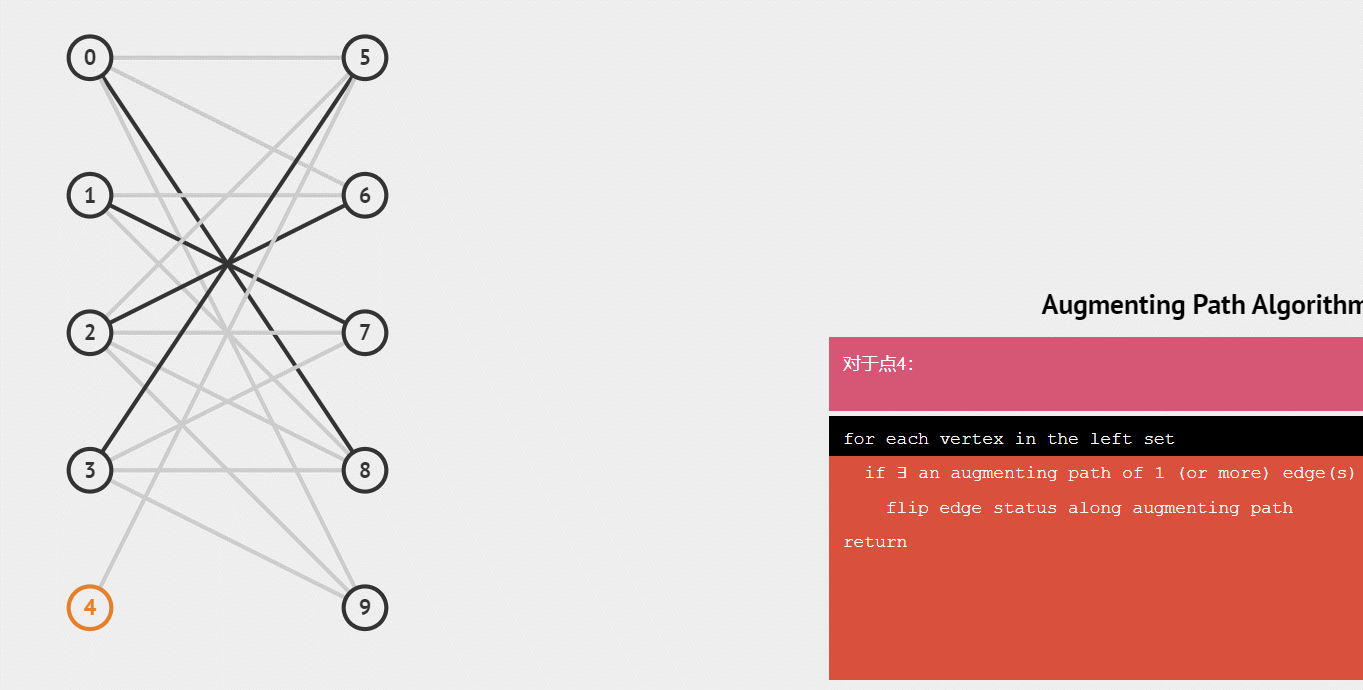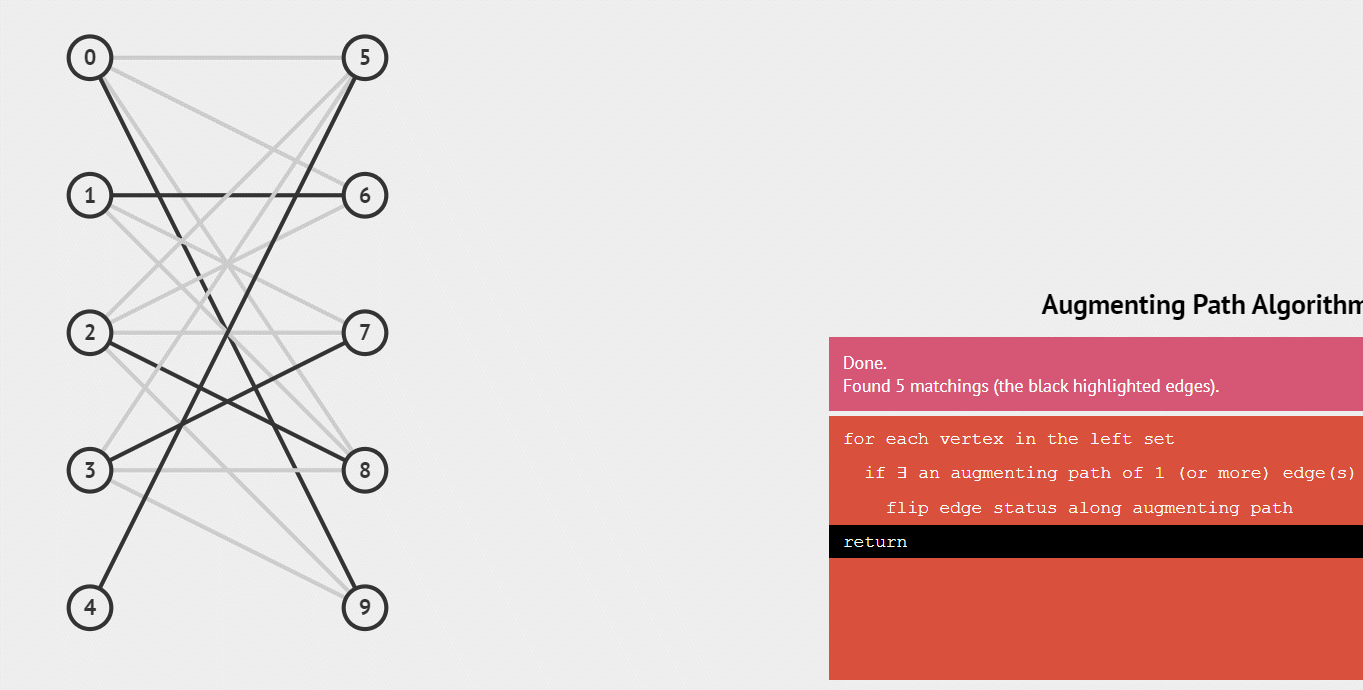
增广路:从一个未匹配点出发,走交替路,如果途径另一个未匹配点(出发的点不算),则这条交替 路称为增广路(agumenting path)。
匈牙利算法
用一个转载的例子来讲解匈牙利算法的流程。
代码实现匈牙利算法
首先是存图模板
//邻接表写法,存稀疏图
int h[N],ne[N],e[N],idx;
//n1,n2分别是两个点集的点的个数
int n1,n2,m;
void add(int a , int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void init()
{
memset(h,-1,sizeof h);
}
//存边只存一边就行了,虽然是无向图。
for(int i = 0 ; i < n1 ; i ++)
{
int a,b;
cin>>a>>b;
add(a,b);
}
接下来看算法模板(c++)
//match[j]=a,表示女孩j的现有配对男友是a
int match[N];
//st[]数组我称为临时预定数组,st[j]=a表示一轮模拟匹配中,女孩j被男孩a预定了。
int st[N];
//这个函数的作用是用来判断,如果加入x来参与模拟配对,会不会使匹配数增多
int find(int x)
{
//遍历自己喜欢的女孩
for(int i = h[x] ; i != -1 ;i = ne[i])
{
int j = e[i];
if(!st[j])//如果在这一轮模拟匹配中,这个女孩尚未被预定
{
st[j] = true;//那x就预定这个女孩了
//如果女孩j没有男朋友,或者她原来的男朋友能够预定其它喜欢的女孩。配对成功,更新match
if(!match[j]||find(match[j]))
{
match[j] = x;
return true;
}
}
}
//自己中意的全部都被预定了。配对失败。
return false;
}
//记录最大匹配
int res = 0;
for(int i = 1; i <= n1 ;i ++)
{
//因为每次模拟匹配的预定情况都是不一样的所以每轮模拟都要初始化
memset(st,false,sizeof st);
if(find(i))
res++;
}
下面用一个gif动图来演示这个整个配对的递归过程
#include<iostream>
#include<cstring>
using namespace std;
const int N = 510 , M = 100010;
int n1,n2,m;
int h[N],ne[M],e[M],idx;
bool st[N];
int match[N];
void add(int a , int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void init()
{
memset(h,-1,sizeof h);
}
int find(int x)
{
//遍历自己喜欢的女孩
for(int i = h[x] ; i != -1 ;i = ne[i])
{
int j = e[i];
if(!st[j])//如果在这一轮模拟匹配中,这个女孩尚未被预定
{
st[j] = true;//那x就预定这个女孩了
//如果女孩j没有男朋友,或者她原来的男朋友能够预定其它喜欢的女孩。配对成功
if(!match[j]||find(match[j]))
{
match[j] = x;
return true;
}
}
}
//自己中意的全部都被预定了。配对失败。
return false;
}
int main()
{
init();
cin>>n1>>n2>>m;
while(m--)
{
int a,b;
cin>>a>>b;
add(a,b);
}
int res = 0;
for(int i = 1; i <= n1 ;i ++)
{
//因为每次模拟匹配的预定情况都是不一样的所以每轮模拟都要初始化
memset(st,false,sizeof st);
if(find(i))
res++;
}
cout<<res<<endl;
}





















 427
427











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








