贪心+基础动态规划(dp)+简单STL运用(栈.队列)--(3)

完全背包

视频讲解<<](https://www.bilibili.com/video/av86427339/?spm_id_from=333.788.videocard.10)
https://www.bilibili.com/video/av86427339/?spm_id_from=333.788.videocard.10
ACM题目链接
https://vjudge.net/contest/353904#overview

1. hdu 1114 http://acm.hdu.edu.cn/showproblem.php?pid=1114
2.hdu 2159 http://acm.hdu.edu.cn/showproblem.php?pid=2159
3. poj 1276 https://vjudge.net/problem/POJ-1276

题目

有N种物品和一个容量为V的背包，每种物品都有无限件可用。第i种物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

基本思路:
完全背包和01背包的区别是一个物品可以被拿无限次,我们之前01背包是拿或者不拿的max,比较,然后我们处理完全背包的时候每个物品拿多少次就好了

每个物品最优拿法=max(不拿,拿一个,拿两个,…,拿n个),抛出个问题,n难道是无限吗?显然不是,大前提是背包总空间或者说处理到第i个物品时剩余空间有限

如果说当前空间最多只能拿n个,那我们的max函数就比较到这个物品拿n个时候就好了

这样一来,无限的问题被我们用背包总空间的限制条件处理成了一个动态的有限问题

其实也算是完全背包转多重背包

这样来就有了第一个递推式

f[i][v]=max{f[i-1][v-kc[i]]+kw[i]|0<=k*c[i]<=v}
2. ①与零一背包不同的是，零一背包中的物品是不可以重复拿取的，只可以拿取当前物品或者不拿取当前物品，不可以拿取多个，完全背包的物品是可以任意拿取多个的来构成不超过背包容量并且构成的总价值是最大的

② 首先我们是可以使用试探的方式来拿取物品的，对于当前的物品我们可以不拿取，拿取一个，拿取两个…直到不能够拿取当前物品了，这种试探的思维我们是可以使用深度优先搜索来进行解决的，但是时间复杂度可能有点高，对于这种经典的求解最大值的问题我们是可以使用动态规划来进行解决的

③ 动态规划的核心是找到dp公式或者状态转移的方程，理解清楚中间的过程是怎么样进行变化的，因为动态规划总是要利用到之前历史上的最佳方案，所以dp数组里面存储的肯定是历史上存储的最佳方案，一开始的时候我们是可以借助excel表格来帮助我们理解dp数组是怎样生成的

④ 我们可以这样想：当前我的背包容量有多少，而且我可以选择的物品的范围是什么，那么这两个变量就可以确定一个值了，我们可以计算出当前背包容量对于当前可以选择的物品范围构成的最大价值

所以借助excel表格来帮助我们理解dp表的生成，其中以物品的质量为{7, 4, 3, 2}，价值为{9, 5, 3, 1}为例，下面是生成的过程：

横坐标是目前的背包容量，纵坐标是当前可以选择的物品的范围，那么excel表格填出来的结果如下：

⑤ 采用的策略是：对于当前的物品我们是可以选择不拿取的，因为可以重复拿取那么我们是可以拿取当前物品的1,2,3…k倍的，并且k * w[i] <= W

• 这样代码应该是三层循环（物品数量，物品种类，背包大小这三个循环），伪代码如下：

•	F[0][] ← {0}  
•	F[][0] ← {0}  
•	for i←1 to N  
•	    do for j←1 to V  
•	        do for k←0 to j/C[i]  
•	           if(j >= k*C[i])  
•	                then F[i][k] ← max(F[i][k],F[i-1][j-k*C[i]]+k*W[i])  
•	return F[N][V]

• 很明显，这样一般情况下会超时，需要转化成时间复杂度比较低的在进行求解
• 经过思考可以想到完全背包可以转化为01背包：
• 因为同种物品可以多次选取，那么第i种物品最多可以选取V/C[i]件价值不变的物品，然后就转化为01背包问题。如果把第i种物品拆成体积为C[i]×2k价值W[i]×2k的物品，其中满足C[i]×2k≤V。即设F[i][j]表示出在前i种物品中选取若干件物品放入容量为j的背包所得的最大价值。那么对于第i种物品的出现，我们对第i种物品放不放入背包进行决策。如果不放那么F[i][j]=F[i-1][j]；如果确定放，背包中应该出现至少一件第i种物品，所以F[i][j]种至少应该出现一件第i种物品,即F[i][j]=F[i][j-C[i]]+W[i]。为什么会是F[i][j-C[i]]+W[i]？因为F[i][j-C[i]]里面可能有第i种物品，也可能没有第i种物品。我们要确保F[i][j]至少有一件第i件物品，所以要预留C[i]的空间来存放一件第i种物品。

看看下面的图

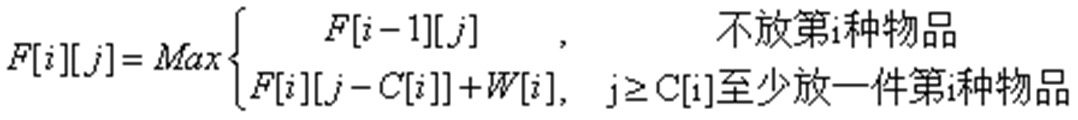
伪代码：
•	  F[0][] ← {0}
•	     F[][0] ← {0}
•	     for i←1 to 
•	         do for j←1 to V
•	             F[i][j] ← F[i-1][j]
•	             if(j >= C[i])
•	                 then F[i][j] ← max(F[i][j],F[i][j-C[i]]+ W[i])
•	      return F[N][V]

时间复杂度的优化：

基本想法：

感兴趣可以看看这个博客
https://blog.csdn.net/ACM_hades/article/details/89190424

最后递推出来公式 :

dp[i][j]=max⁡{dp[i−1][j],dp[i][j−w[i]]+v[i]}

核心代码

void solve()
{
    for(int i=1; i<=n; i++)//n商品数量
        for(int j=1; j<=W; j++)//背包容量
        {
            dp[i][j]=dp[i-1][j];//先赋值不选
            if(w[i]<=j)//如果背包容量大于这个w[i],则至少可以放一个
                dp[i][j]=max(dp[i][j],dp[i][j-w[i]]+v[i]);//比较一下是放好还是不放好
        }
}

时间复杂度：代码的时间复杂度是：O(n*W)

其实了解上面已经可以了,下面可以不用看了

- 背包问题进一步优化：

在完全背包问题中我们的dp[i][j] 只使用了上一行的一个元素dp[i−1][j] 所以可以直接用一维数组实现。

- 核心代码：

void solve()
{
    //初始化
    memset(dp,0,sizeof(dp));
    for(int i=1; i<=n; i++)
        for(int j=w[i]; j<=W; j++)
            dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}

二.多重背包

下篇在介绍吧

https://blog.csdn.net/weixin_43732535/article/details/104192398