本文深入探讨图数据结构，涵盖有向图、无向图、混合图等类型，解析连通性、权重、完全图等概念，以及邻接矩阵与邻接表的实现方式。
数据结构回顾
回顾一下目前为止掌握的学过的数据结构。
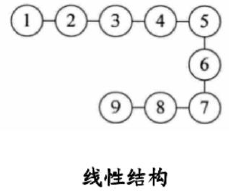
线性结构：数组、链表、栈、队列、哈希表
树形结构：二叉树、B树、堆、Trie、哈夫曼树、并查集
图是不属于以上两类的数据结构。
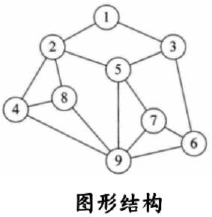
图（Graph）
图由顶点（vertex）和边（edge）组成，通常表示为 G = (V, E)
- G 表示一个图，V 是顶点集，E 是边集
- 顶点集 V 有穷且非空
- 任意两个顶点之间都可以用边来表示它们之间的关系，边集 E 可以为空
以下都属于图。
图结构的应用极其广泛：
- 社交网络
- 地图导航
- 游戏开发
- …
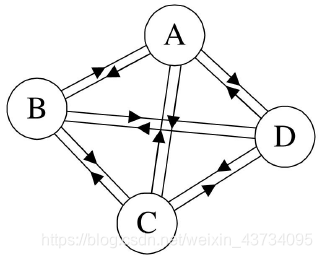
有向图（Directed Graph）
有向图的边是有明确方向的：
有向无环图（Directed Acyclic Graph，简称 DAG）
- 如果一个有向图，从任意顶点出发无法经过若干条边回到该顶点，那么它就是一个有向无环图
出度、入度
出度、入度适用于有向图
出度（Out-degree）
- 一个顶点的出度为 x，是指有 x 条边以该顶点为起点
- 顶点 11 的出度是 3
入度（In-degree）
- 一个顶点的入度为 x，是指有 x 条边以该顶点为终点
- 顶点 11 的入度是 2
无向图（Undirected Graph）
无向图的边是无方向的
无向图可以通过有向图表示出来，但是有向图无法通过无向图来表示。
下面这个有向图就相当于上面的无向图。
混合图（Mixed Graph）
混合图的边可能是无向的，也可能是有向的。
简单图、多重图
平行边
- 在无向图中，关联一对顶点的无向边如果多于1条，则称这些边为平行边
- 在有向图中，关联一对顶点的有向边如果多于1条，并且它们的的方向相同，则称这些边为平行边
多重图（Multigraph）
- 有平行边或者有自环的图
简单图（Simple Graph）
- 既没有平行边也不没有自环的图
- 课程中讨论的基本都是简单图
无向完全图（Undirected Complete Graph）
无向完全图的任意两个顶点之间都存在边
- n 个顶点的无向完全图有 n(n − 1) / 2 条边
- (n − 1) + (n − 2) + (n − 3) + ⋯ + 3 + 2 + 1
有向完全图（Directed Complete Graph）
有向完全图的任意两个顶点之间都存在方向相反的两条边
- n 个顶点的有向完全图有 n(n − 1) 条边
稠密图（Dense Graph）：边数接近于或等于完全图
稀疏图（Sparse Graph）：边数远远少于完全图
有权图（Weighted Graph）
有权图的边可以拥有权值（Weight）
连通图（Connected Graph）
如果顶点 x 和 y 之间存在可相互抵达的路径（直接或间接的路径），则称 x 和 y 是连通的
如果无向图 G 中任意 2 个顶点都是连通的，则称G为连通图
连通分量（Connected Component）
连通分量：无向图的极大连通子图
- 连通图只有一个连通分量，即其自身
- 非连通的无向图有多个连通分量
下面的无向图有 3 个连通分量：
强连通图（Strongly Connected Graph）
如果有向图 G 中任意2个顶点都是连通的，则称G为强连通图
强连通分量（Strongly Connected Component）
强连通分量：有向图的极大强连通子图
- 强连通图只有一个强连通分量，即其自身；非强连通的有向图有多个强连通分量
图的实现方案
图有2种常见的实现方案：
- 邻接矩阵（Adjacency Matrix）
- 邻接表（Adjacency List）
邻接矩阵（Adjacency Matrix）
邻接矩阵的存储方式
- 一维数组存放顶点信息
- 二维数组存放边信息
邻接矩阵比较适合稠密图
- 不然会比较浪费内存
邻接矩阵 – 有权图
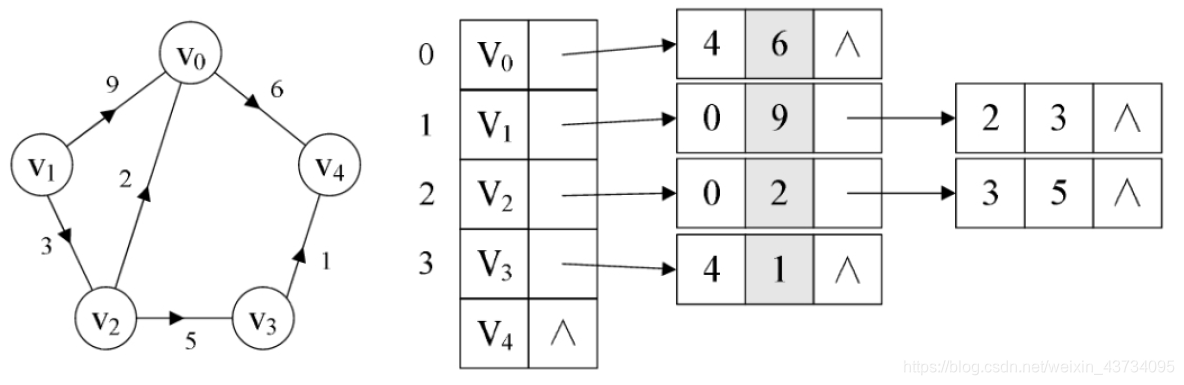
邻接表（Adjacency List）
邻接表 – 有权图
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
