排列组合详解

在笔试题中看到的一个选择题

用1*3的瓷砖密铺3*20的地板有几种方式？

排列组合问题

排列和组合问题，其实是两种问题，区分它们的原则是是否需要考虑顺序的不同。排列问题，考虑顺序；组合问题，不考虑顺序。以下4个问题，哪个是排列，哪个是组合？

Q1: 一套书共有1-6 册，从书架上把它们全部取下。有多少种取法？
Q2: 有5个红球，3个黄球，2个黑球，从中选择2个球。有多少种不同的选择？
Q3: 10个候选人，选3个作为领队，有多少种选择方案？
Q4: 有一把3位数字密码锁，最多需要试多少次才能打开？

以上4个问题，1和4属于排列问题，2和3是组合问题。取书问题中，{1, 2, 3, 4, 5, 6}和{1, 6, 5, 4, 3, 2}，两种方法顺序不同，属于不同的取法，即要考虑顺序不同的排列问题。选球问题中，第1次选黄第2次选黑，和第1次选黑第2次选黄，是相同的选择，即不同考虑顺序不同的组合问题。

此外，考虑是否重复又可分为排列可重复问题、排列不可重复问题、组合可重复问题、组合不可重复问题。例如Q4，{1, 2, 1}是一种密码，数字是可重复的。Q1，取书问题，就无法同一册书取两次，是不可重复的。

排列可重复

那么，何为“可重复”呢？暂且不考虑排列组合，先解释可重复。举个例子，冰淇淋有3种口味可以选择，我可以选择3种相同口味，也可以选择不同口味，每次选择即可相同也可不相同。再举个例子抛硬币3次，很显然，可能会出现3次都是正面，硬币出现正反面是可重复的。典型的问题如，开锁问题，彩票问题，都是排列可重复问题。

排列可重复问题公式如下，每次n种选择，选择r次的排列共有：n^r

这很好理解，一次有 n种选择，第二次有n∗n种选择，……，第 r次有n^r种选择。

排列不可重复

不可重复也很好理解了。例如，打桌球问题，一共15个球，打进所有球有多少种打法。这种情况下，不可能一个球重复打进，第一次击球有15种可能，第二次只有14种，……，最后一次就只有一个球了，只有一种可能。

这个打桌球问题，可以这样理解。首先，共有15个球，全部打完，共有多少种排列？显然，15∗14∗…∗2∗1=15! 。然后考虑，不全部打完呢？打3次有多少种排列，显然15∗14∗13，为了公式的整齐可以写成：

排列不可重复问题更一般的公式如下， n个球，打r次的排列共有：

组合不可重复

组合可重复问题放在最后，先看组合不可重复。先看例子，共有红黄蓝绿黑5种颜色的球，随机取3次有几种颜色组合。{红、绿、黄}和{黄、绿、红}虽然顺序不同，但是相同的组合，即只算一种情况。同时，不可能出现{红、红、黄}，即这是一个不可重复问题。

首先，显然红黄绿是1种组合，我们来看红黄绿有多少种排列。

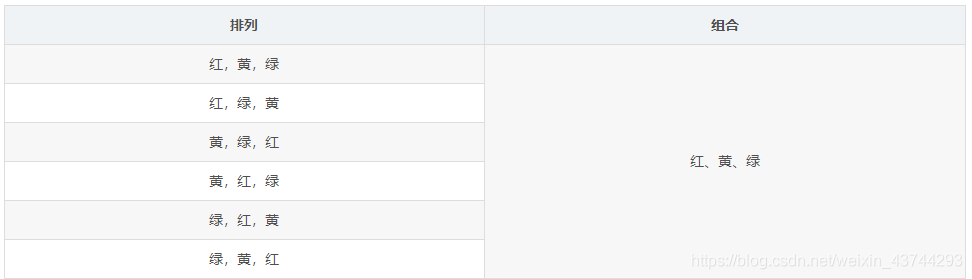
即3∗2∗1=3!种排列，是同1种组合。所以本问题中，首先根据排列不重复问题，我们求出所有的排列：

再除以3!就是我们需要的组合数了。所以组合不重复问题的公式为：

组合可重复

举个例子，有5种冰淇淋口味{咖啡，香草，草莓，香蕉，香芋}，选3次，口味可重复，共有多少种组合。口味分别用字母{C, V, S, B, T}代替，用走方格来简化，◯表示选择当前字符，>表示移动到下一格。

C	V	S	B	T

选择{C, B, B}，可以记作◯>>>◯◯>
选择{V, S, T}，可以记作>◯>◯>>◯>
选择{T, C, T}，由于顺序不重要，所以等于{C, T, T}可以记作◯>>>>◯◯ 。

所以，将问题转化为从头开始走方格到最后一格，◯和>的组合问题。不论怎么选择，移动到最后一格都需要5-1=4步，加上选择的3步，所以共有(5-1)+3=7种可能，其中3个圆圈，共有：

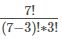
可以转化成组合不重复问题，看作共有(r+n-1)个球，从中选择r个，即：

组合可重复的公式为：

所以解题的关键在于如何将问题转化为我们熟悉的排列组合问题。下面我们再来看一个例子，如何将问题转化。

如果选择{1，2，2}，◯>◯◯>>则代表了在位置1插入1个红球，在位置2插入2个红球，即6个球的组合为{红，白，红，红，白，白}；

如果选择{2，2，2}，>◯◯◯>>则代表在位置2插入3个红球，6个球的位置即为{白，红，红，红，白，白}。
所以，n=4,r=3按照公式：

所以回到一开始的题目。应该怎么算呢？

待续

---

参考文献：
https://www.mathsisfun.com/combinatorics/combinations-permutations.html

本文转载自：https://blog.csdn.net/zeo_m/article/details/80505404?utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromMachineLearnPai2%7Edefault-8.control&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromMachineLearnPai2%7Edefault-8.control