最佳匹配问题-KM算法

最新推荐文章于 2025-04-17 17:03:50 发布

我不叫细胞大液泡了

最新推荐文章于 2025-04-17 17:03:50 发布

阅读量2.7k

点赞数

分类专栏： I like for you to be still

本文链接：https://blog.csdn.net/weixin_43769146/article/details/100641195

版权

KM算法是在最大匹配基础上考虑边权，寻找二分图中匹配边权和最大的解决方案。介绍了一个详细的KM算法入门资源，解释了算法思路：初始化时，左节点赋最大边权，右节点赋0。通过匈牙利算法匹配，冲突时调整边权直至找到匹配。应用实例为HDU2255题目。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

最佳匹配时在最大匹配的基础上，在二分图上增加边权，求出匹配边权和的最大值。
在这里插入图片描述
这里详细的讲解放这个链接km算法入门
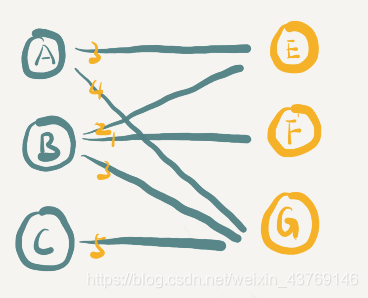
大概思路就是加入左边点的点权（等于最大边权），右边点边权为0，当左右点的边权和等于边权则可以匹配。每次按照匈牙利匹配，当发生冲突时，匈牙利撤回到最后一个点没有可以匹配的边时，左边点边权降低1，右边点边权增加1。再次匹配，若是不可以，继续+1,-1，直到匹配上

HDU2255

#include<iostream>
#include<vector>
#include<string.h>
#include<algorithm>
#include<stdio.h>
using namespace std;
const int N=302;
const int inf=1e6;
int g[N][N], used[N],rela[N];
int n;
int topx[N],topy[N],usex[N],usey[N],slack[N];
bool find(int x){
   
    usex[x]=1;                //标记参与 
    for(int i=1;i<=n;i++){
       
        if(usey[i]==1