POJ1144(network)

题目传送门

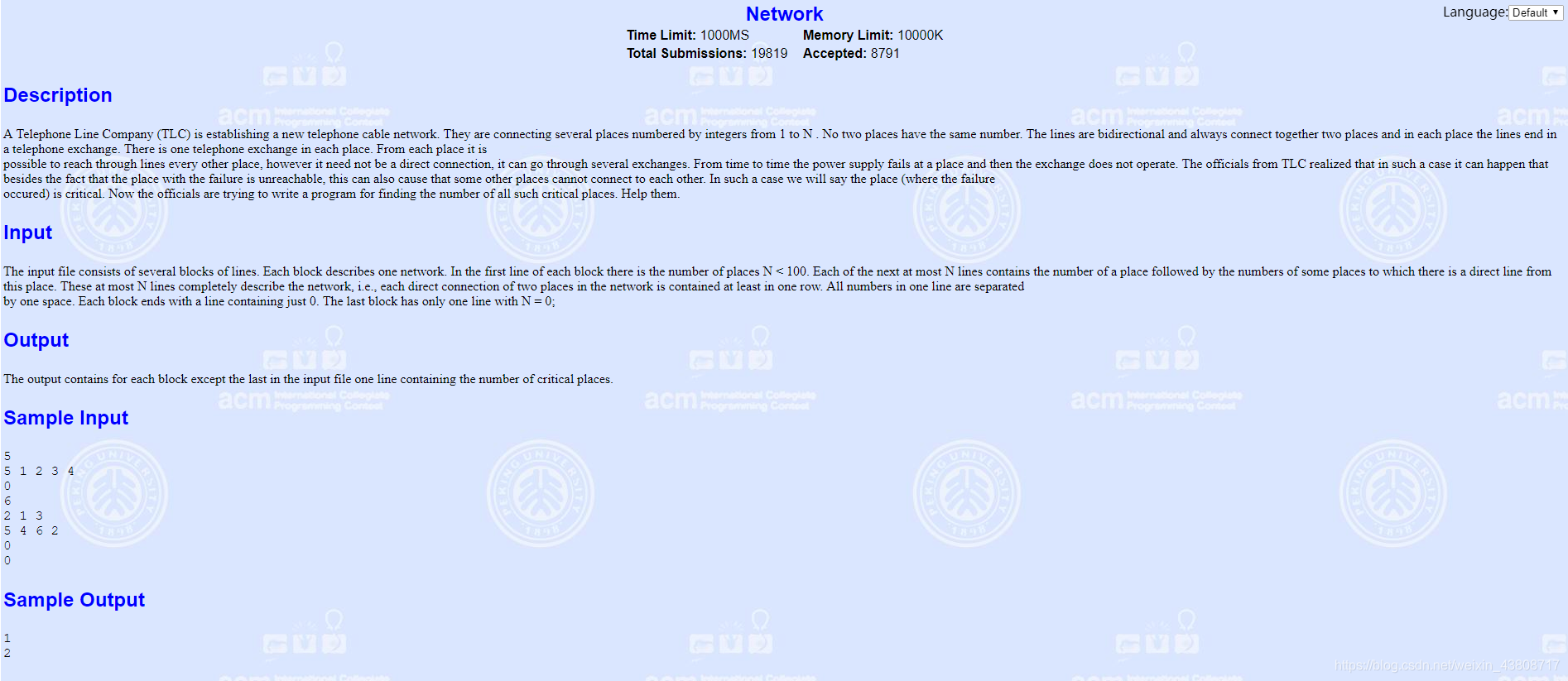
思路

无向图求割点裸题，直接tarjan生成一颗深度优先生成树。判断当前子节点能不能返回到父节点的父节点或者更远，也就是能回到除去父节点之外更远的祖先。

1. 如果子节点能回到祖先说明父节点不是割点，去掉父节点这个图依然连通。
2. 如果子节点不能回到祖先，说明父节点是割点，去掉父节点这个连通图被分成2个以上的连通块。

这题除了输入有点恶心之外其他的没啥，搞不动为啥要这样输入。

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <string>
#include <vector>
using namespace std;
struct edge{
	int to;
	int next;
}e[500];
int head[105];
int dfn[105];				//节点的访问顺序 
int low[105];				//子节点能回到祖先的序号 
bool cut[105];				//割点 
int n,cnt,tot,ans;
inline void clear_set()
{
	cnt = tot = ans = 0;
	memset(head,-1,sizeof(head));
	memset(dfn,0,sizeof(dfn));
	memset(low,0,sizeof(low));
	memset(cut,false,sizeof(cut));
}
inline void addedge(int x,int y)
{
	e[tot].to = y;
	e[tot].next = head[x];
	head[x] = tot++;
}
inline void tarjan(int x,int fx)
{
	dfn[x] = low[x] = ++cnt;
	int child = 0;
	for(int i = head[x];~i;i = e[i].next){
		int y = e[i].to;
		if(!dfn[y]){
			child++;
			tarjan(y,x);
			low[x] = min(low[x],low[y]);
			if(low[y] >= dfn[x] && x != 1){
				if(!cut[x]){
					ans++;
				}
				cut[x] = true;
			}
		}
		else if(dfn[y] < dfn[x] && y != fx){
			low[x] = min(low[x],dfn[y]);
		}
	}
	if(child >= 2 && x == 1){
		if(!cut[x]){
			ans++;
		}
		cut[x] = true;
	}
}
int main()
{
	while(~scanf("%d",&n) && n){
		clear_set();
		int x,y;
		while(scanf("%d",&x) && x != 0){
			while(getchar() != '\n'){
				scanf("%d",&y);
				addedge(x,y);addedge(y,x);
			}
		} 
		tarjan(1,-1);
		printf("%d\n",ans);
	}
	return 0;
}  

愿你走出半生，归来仍是少年~