山东大学程序设计第十周作业

最新推荐文章于 2024-03-21 17:54:17 发布

原创最新推荐文章于 2024-03-21 17:54:17 发布 · 292 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #动态规划 #数据结构 #c++

程序设计作业专栏收录该内容

11 篇文章

订阅专栏

本文解析了三道游戏算法题目，包括转换数字、寻找最长递增子序列与最长公共子序列、以及拿数问题II，提供了详细的解题思路和C++代码实现。

第一题

签到题

东东在玩游戏“Game23”。

在一开始他有一个数字n，他的目标是把它转换成m，在每一步操作中，他可以将n乘以2或乘以3，他可以进行任意次操作。输出将n转换成m的操作次数，如果转换不了输出-1。

Input

输入的唯一一行包括两个整数n和m（1<=n<=m<=5*10^8).

Output

输出从n转换到m的操作次数，否则输出-1.

Example

input
120 51840
output
7
input
42 42
output
0
input
48 72
output
-1

解题思路

签到题思路比较简单，用m除以n，看是否为整数，如果是整数再继续判断是否可以被3整除或被2整除，记录相除的次数，如果出到最后为1则可以转换，否则不可以。

代码实现

#include<iostream>
using namespace std;
int main()
{
    int m, n, ans = 0;
    cin >> n >> m;
    if(n==m) cout << 0;
    else if(m%n!=0) cout << -1;
    else
    {
        int mod = m / n;
        while(mod!=1)
        {
			if (mod%3==0) {
				mod /= 3;
				ans++;
			}
			else if(mod%2==0){
				mod /= 2;
				ans++;
			}
            else
            {
                cout << -1;
                return 0;
            }

        }
        cout << ans;
    }
    return 0;
}

第二题

LIS&LCS问题

东东有两个序列A和B。

他想要知道序列A的LIS和序列AB的LCS的长度。

注意，LIS为严格递增的，即a1<a2<…<ak(ai<=1,000,000,000)。

Input

第一行两个数n，m（1<=n<=5,000,1<=m<=5,000）
第二行n个数，表示序列A
第三行m个数，表示序列B

Output

输出一行数据ans1和ans2，分别代表序列A的LIS和序列AB的LCS的长度

Example

input
5 5
1 3 2 5 4
2 4 3 1 5
output
3 2

解题思路

LIS问题的状态转移方程为：
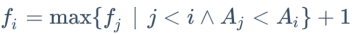
在这里插入图片描述
LIS的长度为max{f[i], i=1…n }，其中fi 表示以 Ai 为结尾的最长上升序列的方程。

LCS问题的状态转移方程为：
if i0||j0,f[i][j]=0
else if Ai == Bj ，f[i][j] = f[i-1][j-1] + 1
else f[i][j] = max(f[i-1][j], f[i][j-1])
然后f[m][n]的值即为LCS 的长度

代码实现

#include<iostream>
using namespace std;
int dp[5010][5010];//.......
int main()
{
    int n, m;
    cin >> n >> m;
    long long a[5010], b[5010];
    int ans=1;
    int length[5010];
    for (int i = 1;i<=n;i++) cin >> a[i];
    for (int i = 1;i<=m;i++) cin >> b[i];
    for(int i = 1;i<=n;i++) length[i] = 1;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j < i; j++)
            if (a[j] < a[i] && length[j] + 1 > length[i])
                length[i] = length[j] + 1;
        ans = max(ans, length[i]);
    }
	cout << ans << " ";
    for (int i = 0; i <= n; i++) {
		for (int j = 0; j <= m; j++) {
			if (i == 0 || j == 0) dp[i][j] = 0;
			else if (a[i] == b[j])
				dp[i][j] = dp[i - 1][j - 1] + 1;
			else
				dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
		}
	}
	cout << dp[n][m] << endl;
	return 0;
}

第三题

拿数问题

YJQ 上完第10周的程序设计思维与实践后，想到一个绝妙的主意，他对拿数问题做了一点小修改，使得这道题变成了拿数问题 II。

给一个序列，里边有 n 个数，每一步能拿走一个数，比如拿第 i 个数， Ai = x，得到相应的分数 x，但拿掉这个 Ai 后，x+1 和 x-1 (如果有 Aj = x+1 或 Aj = x-1 存在) 就会变得不可拿（但是有 Aj = x 的话可以继续拿这个 x）。求最大分数。

Input

第一行包含一个整数 n (1 ≤ n ≤ 105)，表示数字里的元素的个数

第二行包含n个整数a1, a2, …, an (1 ≤ ai ≤ 105)

Output

输出一个整数：n你能得到最大分值。

Example

input
2
1 2
output
2
input
3
1 2 3
output
4
input
9
1 2 1 3 2 2 2 2 3
output
10

解题思路

状态转移方程为：
dp[i] = max(dp[i - 1], dp[i - 2] + i * sum[i])
dp数组记录每一个数出现的次数，dp[i]记录取小于等于i的数时的最大分数。

代码实现

#include <iostream>
using namespace std;

long long dp[100010],a[100010];
int main()
{
	long long n, t, sum, mx=0;
	cin>>n;
	for(long long i=0;i<n;i++)
	{
        cin >> t;
        a[t]++;
		mx = max(mx, t);
	}
	dp[0] = 0, dp[1] = a[1];
	for(long long i=2;i<=mx;i++)
	{
		t =a[i]*i;
		dp[i] = max(dp[i-1], dp[i-2]+t);
	}
    cout << dp[mx];
	return 0;
}