栈和队列求解迷宫问题（数据结构学习笔记）

---

迷宫问题

给定一个M*N的迷宫图、入口与出口、行走规则。求一条从指定入口到出口的路径（这里M=8,N=8）,所求路径必须是简单路径，即路径不重复 (为了方便算法起见，在整个迷宫外围加上一堵墙）

这里分别使用栈和队列两种方法求解迷宫问题，并比较两种算法的具体体现。

“栈”求解迷宫问题

行走规则

上、下、左、右相邻的方块行走。其中（i,j）表示一个方块

算法思路

1、用二维数组存放0,1来分别表示迷宫中可走方块以及不可走方块。

2、从入口处开始，顺时针方向去试探当前方块的四个方位

3、在当前位置寻找四个方位中的可走方块。
若当前试探方位可走。则将该试探方位的方块入栈，并将此时走过的方块置为不可走（这里将值置为-1），以防止两个方块来回进入死循环，此时试探方位的方块在栈的顶部，再用栈顶方块继续对四个方位进行试探。
若当前方块的四个试探方位都无法前进。则将当前方块退栈，并将退栈方块的值恢复为0，然后找此时栈顶方块的其他可能的相邻方块。

当所有相邻方块都不能走时的情况

算法代码

栈的定义

//定义方块类型
typedef struct
{
    int i;  //当前方块的行号
    int j;  //当前方块的列好
    int dj; //下个可走相邻方位的方位号
}Box;
//定义顺序栈类型
typedef struct
{
    Box data[MaxSize];
    int top;    //栈顶指针
}StType;

算法设计

bool mgpath(int xi,int yi,int xe,int ye)
{
	Box path[10000],e;	//path数组用来记录迷宫路径，e用来记录栈顶元素 
	StType *st;		//定义栈st 
	int i,j,di;		//i,j,di用于记录栈顶元素 
	int in,jn;		//用于记录下一方位的方块行列坐标 
	int k;				 
	int find;	//记录是否找到相邻可走元素 
	InitStack(st);	//初始化栈
	
	e.i=xi,e.j=yi,e.di=-1;
	Push(st,e);
	mg[xi][yi]=-1;
	
	
	while(!StackEmpty(st)){
		GetTop(st,e);	//取出栈顶元素 
		i=e.i,j=e.j,di=e.di;
		if(i==xe&&j==ye){	//已到达终点 
			printf("一条迷宫路径如下:\n");
			k=0;
			while(!StackEmpty(st)){
				Pop(st,e);
				path[k++]=e;
			}
			while(k>=1)
			{
				k--;
		                printf("\t(%d,%d)",path[k].i,path[k].j);
				if((k+2)%5==0)	
					printf("\n");	//每输出5个方块后换一行 
			}
			printf("\n");
			DestroyStack(st);	//销毁栈 
			return true;
		}
		
		find=0; //初始化为0，未找到可走相邻方块 
		while(di<4&&find==0){	 
			di++;
			switch(di){
				case 0:{in=i-1,jn=j;break;}
				case 1:{in=i;jn=j+1;break;}
				case 2:{in=i+1;jn=j;break;}
				case 3:{in=i;jn=j-1;break;}
			}
			if(mg[in][jn]==0)	//找到可走相邻方块 
				find=1;	
		}
		
		if(find){	//找到可走相邻方块 
			st->data[st->top].di=di; //修改原栈顶元素的di值 
			e.i=in,e.j=jn,e.di=-1;
			Push(st,e);	//入栈操作 
			mg[in][jn]=-1; 
		}
		else{	//没有可走相邻方块 
			Pop(st,e);	//退栈操作 
			mg[e.i][e.j]=0;	//将退栈方块位置的值恢复为 0 
		}
	}
	DestroyStack(st);	//销毁栈 
	return false;	//表示没有可走路径，返回false 
}

完整代码

#include <stdio.h>
#include <stdlib.h>
#define M 8
#define N 8

typedef struct
{
	int i;
	int j;
	int di;
}Box;

typedef struct
{
	Box data[10000];
	int top;
}StType;

int mg[M+2][N+2]=
	{	{1,1,1,1,1,1,1,1,1,1},
		{1,0,0,1,0,0,0,1,0,1},
		{1,0,0,1,0,0,0,1,0,1},
		{1,0,0,0,0,1,1,0,0,1},
		{1,0,1,1,1,0,0,0,0,1},
		{1,0,0,0,1,0,0,0,0,1},
		{1,0,1,0,0,0,1,0,0,1},
		{1,0,1,1,1,0,1,1,0,1},
		{1,1,0,0,0,0,0,0,0,1},
		{1,1,1,1,1,1,1,1,1,1}
	};

//初始化栈 
void InitStack(StType *&st)
{
	st=(StType *)malloc(sizeof(StType));
	st->top=-1;
}
//取出栈顶元素 
void GetTop(StType *&st,Box &e)
{
	e=st->data[st->top];
}
//入栈 
void Push(StType *&st,Box &e)
{
	st->top++;
	st->data[st->top]=e;
}
//出栈 
void Pop(StType *&st,Box &e)
{
	e=st->data[st->top];
	st->top--;
}
//销毁栈 
void DestroyStack(StType *&st)
{
	free(st);
}
//检验栈是否为空 
bool StackEmpty(StType *&st)
{
	if(st->top==-1)
		return true;
	
	return false;
}

bool mgpath(int xi,int yi,int xe,int ye)
{
	Box path[10000],e;	//path数组用来记录迷宫路径，e用来记录栈顶元素 
	StType *st;		//定义栈st 
	int i,j,di;		//i,j,di用于记录栈顶元素 
	int in,jn;		//用于记录下一方位的方块行列坐标 
	int k;				 
	int find;	//记录是否找到相邻可走元素 
	InitStack(st);	//初始化栈
	
	e.i=xi,e.j=yi,e.di=-1;
	Push(st,e);
	mg[xi][yi]=-1;
	
	
	while(!StackEmpty(st)){
		GetTop(st,e);	//取出栈顶元素 
		i=e.i,j=e.j,di=e.di;
		if(i==xe&&j==ye){	//已到达终点 
			printf("一条迷宫路径如下:\n");
			k=0;
			while(!StackEmpty(st)){
				Pop(st,e);
				path[k++]=e;
			}
			while(k>=1)
			{
				k--;
				printf("\t(%d,%d)",path[k].i,path[k].j);
				if((k+2)%5==0)	
					printf("\n");	//每输出5个方块后换一行 
			}
			printf("\n");
			DestroyStack(st);	//销毁栈 
			return true;
		}
		
		find=0; //初始化为0，未找到可走相邻方块 
		while(di<4&&find==0){	 
			di++;
			switch(di){
				case 0:{in=i-1,jn=j;break;}
				case 1:{in=i;jn=j+1;break;}
				case 2:{in=i+1;jn=j;break;}
				case 3:{in=i;jn=j-1;break;}
			}
			if(mg[in][jn]==0)	//找到可走相邻方块 
				find=1;	
		}
		
		if(find){	//找到可走相邻方块 
			st->data[st->top].di=di; //修改原栈顶元素的di值 
			e.i=in,e.j=jn,e.di=-1;
			Push(st,e);	//入栈操作 
			mg[in][jn]=-1; 
		}
		else{	//没有可走相邻方块 
			Pop(st,e);	//退栈操作 
			mg[e.i][e.j]=0;	//将退栈方块位置的值恢复为 0 
		}
	}
	DestroyStack(st);	//销毁栈 
	return false;	//表示没有可走路径，返回false 
}

int main()
{
	if(!mgpath(1,1,M,N))
		printf("该迷宫问题没有解");
		
	return 0;
}

最终迷宫路径

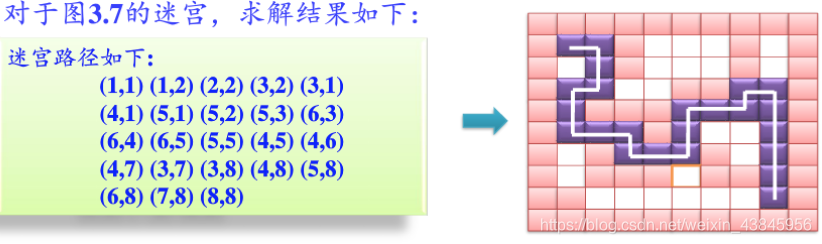
算法总结

• 很显然栈求解迷宫问题，只是给出解决迷宫问题的其中一条路径，并非最优路径

---

“队列”求解迷宫问题

例如此迷宫：

算法思路

将所有相邻的可走方块进入队列，在队列中一层一层的去从出口反向寻找入口（要记录当前此可走相邻方块的前一个方块位置）

算法代码

队列定义

typedef struct
{
	int i,j;	//记录方块的行数与列数 
	int pre;	//记录本路径上一方块在队列中的下标 
}Box; 

typedef struct
{
	Box data[1000];
	int front,rear;	//队头队尾指针 
}Que;

算法设计

//迷宫算法函数
bool mgpath1(int xi,int yi,int xe,int ye)
{
	Box e;
	int i,j,pre;
	Que *qu;
	InitQue(qu);	//初始化队列 
	
	//起点入队
	e.i=xi,e.j=yi,e.pre=-1;	
	mg[xi][yi]=-1;
	Push(qu,e);		 
	
	while(!EmptyQue(qu)){	//队列不空则循环 
		Pop(qu,e);	//队首元素出队 
		i=e.i,j=e.j,pre=e.pre;	//记录当前队首元素的方块类 
		if(i==xe&&j==ye){	//队首元素为出口则输出路径 
			print(qu,qu->front);	//输出路径函数 
			return true;
		}
		
		int d=-1;
		int in,jn;
		while(d<4){	//每个方位进行试探 
			d++;
			switch(d){
				case 0:{in=i-1,jn=j;break;}
				case 1:{in=i;jn=j+1;break;}
				case 2:{in=i+1;jn=j;break;}
				case 3:{in=i;jn=j-1;break;}
			}
			if(mg[in][jn]==0){	//找到可走相邻方块(in,jn)就入队 
				e.i=in,e.j=jn,e.pre=qu->front;
				Push(qu,e);
				mg[in][jn]=-1;	//将其赋值-1，以避免来回重复搜索 
			}
		}
	}
	DestroyQue(qu);	//销毁队列 
	return false;
}
//输出路径函数
void print(Que *&qu,int k)
{
	int j;
	//反向寻找最短路径 
	while(k!=-1){
		j=k;
		k=qu->data[k].pre;
		qu->data[j].pre=-1;	//将找到的路径上的方块的pre成员置为-1 
	}
	
	k=0;
	int ns=0;
	while(k<1000){	//遍历整个队列输出pre成员为-1的方块坐标 
		if(qu->data[k].pre==-1){
			ns++;
			printf("\t(%d,%d)",qu->data[k].i,qu->data[k].j);
			if(ns%5==0)	 printf("\n");	//每输出5个元素后换一行 
		}
		k++;
	}
	printf("\n");
}

完整代码

#include <stdio.h>
#include <stdlib.h>
#define M 4
#define N 4

typedef struct
{
	int i,j;	//记录方块的行数与列数 
	int pre;	//记录本路径上一方块在队列中的下标 
}Box; 

typedef struct
{
	Box data[1000];
	int front,rear;	//队头队尾指针 
}Que;

int mg[M+2][N+2]=
	{	{1, 1, 1, 1, 1, 1},
		{1, 0, 0, 0, 1, 1},
		{1, 0, 1, 0, 0, 1},
		{1, 0, 0, 0, 1, 1},
		{1, 1, 0, 0, 0, 1},
		{1, 1, 1, 1, 1, 1}
	};

void InitQue(Que *&qu)
{
	qu=(Que *)malloc(sizeof(Que));
	qu->front=qu->rear=-1;
}

bool EmptyQue(Que *&qu)
{
	return (qu->front==qu->rear);
}

bool Push(Que *&qu,Box &e)
{
	if(qu->rear>999)
		return false;
	e.pre=qu->front;
	qu->rear++;
	qu->data[qu->rear]=e;
	return true;
}

bool Pop(Que *&qu,Box &e)
{
	if(EmptyQue(qu))
		return false;
	qu->front++;
	e=qu->data[qu->front];
	return true;
}

void print(Que *&qu,int k)
{
	int j;
	//反向寻找最短路径 
	while(k!=-1){
		j=k;
		k=qu->data[k].pre;
		qu->data[j].pre=-1;	//将找到的路径上的方块的pre成员置为-1 
	}
	
	k=0;
	int ns=0;
	while(k<1000){	//遍历整个队列输出pre成员为-1的方块坐标 
		if(qu->data[k].pre==-1){
			ns++;
			printf("\t(%d,%d)",qu->data[k].i,qu->data[k].j);
			if(ns%5==0)	 printf("\n");	//每输出5个元素后换一行 
		}
		k++;
	}
	printf("\n");
}

void DestroyQue(Que *&qu)
{
	free(qu);
}

bool mgpath1(int xi,int yi,int xe,int ye)
{
	Box e;
	int i,j,pre;
	Que *qu;
	InitQue(qu);	//初始化队列 
	
	//起点入队
	e.i=xi,e.j=yi,e.pre=-1;	
	mg[xi][yi]=-1;
	Push(qu,e);		 
	
	while(!EmptyQue(qu)){	//队列不空则循环 
		Pop(qu,e);	//队首元素出队 
		i=e.i,j=e.j,pre=e.pre;	//记录当前队首元素的方块类 
		if(i==xe&&j==ye){	//队首元素为出口则输出路径 
			print(qu,qu->front);	//输出路径函数 
			return true;
		}
		
		int d=-1;
		int in,jn;
		while(d<4){	//每个方位进行试探 
			d++;
			switch(d){
				case 0:{in=i-1,jn=j;break;}
				case 1:{in=i;jn=j+1;break;}
				case 2:{in=i+1;jn=j;break;}
				case 3:{in=i;jn=j-1;break;}
			}
			if(mg[in][jn]==0){	//找到可走相邻方块(in,jn)就入队 
				e.i=in,e.j=jn,e.pre=qu->front;
				Push(qu,e);
				mg[in][jn]=-1;	//将其赋值-1，以避免来回重复搜索 
			}
		}
	}
	DestroyQue(qu);	//销毁队列 
	return false;
}

int main()
{
	if(!mgpath1(1,1,M,N))
		printf("此迷宫问题无解");
		
	return 0;
}

最终迷宫路径（小迷宫）

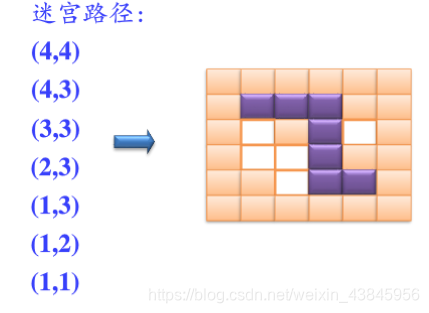
最终迷宫路径（原题迷宫）

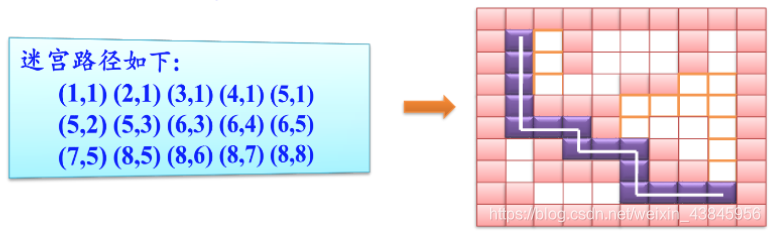
算法总结

• 队列求解迷宫问题可以解决迷宫问题中最优（短）路径解的问题

• 学习数据结构教程（第五版）——李春葆教授主编

• 图片来源于MOOC，数据结构——武汉大学——李春葆教授

• （如若侵权可联系QQ删除）