三维重建之贪婪投影三角化_三角化重建-CSDN博客

本文链接：https://blog.csdn.net/weixin_43850240/article/details/148003103

三个前提假设：

局部均匀。每个点周围最近和最远的点的距离比均小于一定的值，该值假定为u。假设1是为了保证在局部生长时，尽可能地找到周围应该连接的顶点。
两个表面之间的最近距离应该保证一定阈值（um）以上，其中m为某点到其所在表面最近点的距离。每个点的m是不一样的，具体的计算见步骤3。
物体表面是相对平滑的，一个顶点链接的两个三角形之间的法向量不超过90度。假设2和假设3的目的见下所述。

四种点类型：

自由点（free）：没有与任何三角形连接的点。
边缘点（fringe）：没有被选择成为参考点的普通边缘点。
边界点（boundary）已经被选择称为过参考点的边缘点。之所以该点还是边缘点，可能是由于角度准则等原因，未连接一部分顶点，造成该点成为边缘点。
完成点（completed）：完成了连接的点，且不位于边界线上。

上述四类不包括参考点，参考点是每次迭代时，从边缘点中选择出进行该点周围区域三角剖分的顶点。

两条执行准则：

任何的自由点、边缘点和边界点都不可以在三角形的内部。（这里有点疑惑，完成点可以，应该也不可以啊？）
每次迭代结束的时候，参考点成为一个边界或完全点。

七步执行过程：

使用一个桶分类的方式来存储所有的输入顶点。使用一个2D像素矩阵保存所有的顶点，相同像素坐标的顶点按照深度进行排序。其实就是类似于PPLL算法。这个步骤是一个全局的操作，为了便于进行下一步的粗过滤。
初始状态，任选一个点作为参考点。
寻找参考点周围可被连接的点，这里我们简称为感兴趣点。从全局的顶点中寻找到感兴趣点，包含粗过滤和细过滤两个步骤。粗过滤：寻找每个参考点指定范围内的点。首先利用步骤1中得到的桶进行快速的排除。以参考点作为中心，um作为半径检查一个轴对称框内的顶点。选择出此框内的所有自由点、边界点和边缘点。细过滤：通过粗过滤的顶点，如果到参考点的空间欧氏距离（就是三维距离）小于um，那么通过细过滤，将进行下一步的三角化，即细过滤的范围说一个球，此范围表示未SR。在计算每个参考点的m时，如果参考点是自由点（初始），则是范围内的最近点距离；如果参考点是边界点，则m为已连接线的最短距离。通过细过滤的感兴趣点集合成为CR。
将参考点和感兴趣点沿着法向量方向投影到一个二维平面上。每个二维平面上的投影点与三维点一一对应。
进行角度的排序。每个感兴趣点与参考点形成一个向量，这个方向与X轴方向形成一个夹角，按照此夹角对感兴趣点进行排序。理论上顺序连接这些感兴趣点和参考点，形成三角形。为了避免三角形的重叠和自交叉，只有通过点可见性测试的感兴趣点才能参与三角化。此外如果只是通过角度进行连接，往往会形成很多狭长的三角形。为了优化三角形的质量，需要按照角度准则进行处理。
三角化：顺序连接。但是如果感兴趣点和参考点形成的角度超过了最大角度，将不会被连接形成一个三角形。这个最大角度描述了模型中孔洞的特性，通常设置为120°。然后将所有CR中的自由点被标记为fringe点，添加到fringe点队列中。
从fringe队列中选择一个作为参考点，重复（2）-（6）。

假设2和假设3正是为了满足（4）和（5）步骤，避免投影后的点出现乱序。如果没有假设2，那么两层的点被视为同一层的点进行连接，造成很大的形状错误。如果没有（3），那么点的法向量与每个面的法向量差异将会很大。不正确的方向投影很大程度，会造成点的错误重叠（投影后点的顺序和真实的面上顺序不一致）。

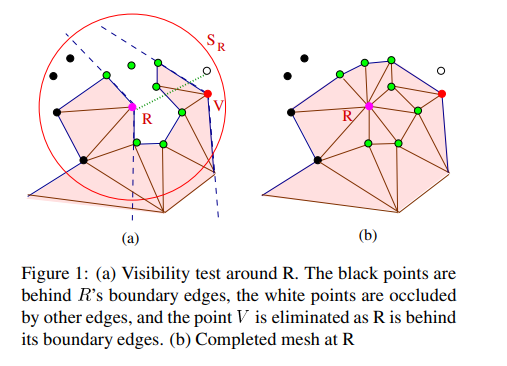
点可见性测试：（1）位于参考点边界确定的不可见区域外的感兴趣点不参与连接；（2）如果参考点位于感兴趣点边界确定的不可见区域，感兴趣点不参与连接；（3）感兴趣点和参考点的连线与其他边有交叉，不参与连接。为了简化检测，这里可以只检测连线和SR范围内边界线的相交情况，无需与所有SR范围内的线进行相交检测，论文有证明。简单理解即：穿过内部的边，一定需要穿过边界的边，因此检测边界边即可）。

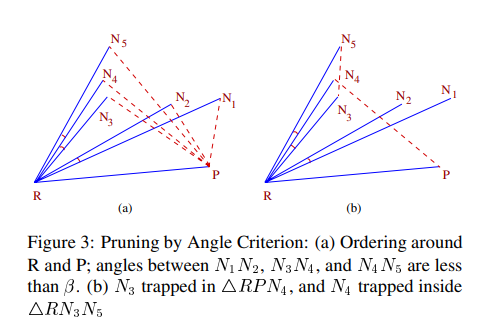
角度准则：如果形成的三角形小于设置的最小角度，那么这个三角形倾向于不保留。在连接时将去除该三角形的一个或两个感兴趣点。但去除的前提是去除了感兴趣点，剩余感兴趣点形成的三角形集合内部不能存在该感兴趣点。论文中给出了一种简单的伪代码。如下所示简而言之，感兴趣点按照参考点R进行排序，然后感兴趣点再按照点P进行排序。如果一点N按照P的排序小于在R下的排序，则说明RPN内部会存在其他感兴趣点，因此不能直接连接RPN。如果所示的RPN5内部会存在N4和N3，因此不能连接RPN5，以此类推。

PCL代码实现：

首先根据点云计算法向量，然后创建算法对象并设置算法参数，最后调用reconstruct接口获得接口。从参数设置上可见PCL中的实现比原论文更为复杂，如支持设置边的最大长度、感兴趣点的上限等，支持更精细的过滤。

#include<iostream>
#include<pcl/io/pcd_io.h>
#include <pcl/io/ply_io.h>
#include<pcl/point_types.h>
#include <pcl/kdtree/kdtree_flann.h>
#include <pcl/features/normal_3d.h>
#include <pcl/io/obj_io.h>
#include <pcl/surface/gp3.h>
#include <pcl/visualization/pcl_visualizer.h>

int main(int argc, char** argv) {
    pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>());
    pcl::PCLPointCloud2 cloud_blob;

    
    //*打开点云文件
    if (pcl::io::loadPCDFile(argv[1], cloud_blob) == -1) {
        PCL_ERROR("Couldn't read file rabbit.pcd\n");
        return(-1);
    }
    pcl::fromPCLPointCloud2(cloud_blob, *cloud);

    //法线估计对象 使用PCA算法来计算法向量
    pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> n;
    //存储估计的法线
    pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);
    //定义kd树指针
    pcl::search::KdTree<pcl::PointXYZ>::Ptr tree(new pcl::search::KdTree<pcl::PointXYZ>);
    tree->setInputCloud(cloud);
    n.setInputCloud(cloud);
    n.setSearchMethod(tree);
    n.setKSearch(20);
    //估计法线存储到其中
    n.compute(*normals);//Concatenate the XYZ and normal fields*
    pcl::PointCloud<pcl::PointNormal>::Ptr cloud_width_normals(new pcl::PointCloud<pcl::PointNormal>);
    //链接字段
    pcl::concatenateFields(*cloud, *normals, *cloud_width_normals);

    //定义搜索树对象
    pcl::search::KdTree<pcl::PointNormal>::Ptr tree2(new pcl::search::KdTree<pcl::PointNormal>);
    //点云构建搜索树
    tree2->setInputCloud(cloud_width_normals);

    //定义三角化对象
    pcl::GreedyProjectionTriangulation<pcl::PointNormal> gp3;
    //存储最终三角化的网络模型
    pcl::PolygonMesh triangles;
    gp3.setSearchRadius(200.0f);//设置连接点之间的最大距离，（即是三角形最大边长）
    //设置各种参数值
    gp3.setMu(2.5f);
    gp3.setMaximumNearestNeighbors(100);
    gp3.setMaximumSurfaceAngle(M_PI_4);//45°，共同顶点三角形角度
    gp3.setMinimumAngle(M_PI / 18);
    gp3.setMaximumAngle(2 * M_PI / 3);
    gp3.setNormalConsistency(false);

    //设置搜索方法和输入点云
    gp3.setInputCloud(cloud_width_normals);
    gp3.setSearchMethod(tree2);

    //执行重构，结果保存在triangles中
    gp3.reconstruct(triangles);

    //保存网格图  
    //pcl::io::saveOBJFile("result.obj", triangles);
    std::string output_dir = "cloud_mesh.ply";
    std::string sav = "saved mesh in:";
    sav += output_dir;
    pcl::console::print_info(sav.c_str());
    std::cout << std::endl;

    //保存为ply文件格式
    pcl::io::savePLYFileBinary(output_dir.c_str(), triangles);

    // 显示结果图  
    boost::shared_ptr<pcl::visualization::PCLVisualizer> viewer(new pcl::visualization::PCLVisualizer("MAP3D MESH"));
    ////设置背景;
    viewer->setBackgroundColor(0, 0, 0);
    //设置显示的网格
    viewer->addPolygonMesh(triangles, "my");
    //viewer->initCameraParameters();
    while (!viewer->wasStopped()) {
        viewer->spin();
    }
    std::cout << "success" << std::endl;
    return 0;
}

参考文献：

A Fast and Efficient Projection-Based Approach for Surface Reconstruction（Sci-Hub | | 10.1109/sibgra.2002.1167141）